1 . 已知 数列满足
数列满足 ,
,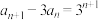 .
.
(1)证明:数列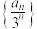 为等差数列;
为等差数列;
(2)求数列 的前n项和
的前n项和 .
.
 数列满足
数列满足 ,
,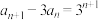 .
.(1)证明:数列
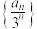 为等差数列;
为等差数列;(2)求数列
 的前n项和
的前n项和 .
.
您最近一年使用:0次
2 . 数列 满足
满足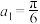 ,
,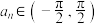 ,
,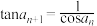 ,
,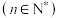 .
.
(1)证明:数列 为等差数列,并求数列
为等差数列,并求数列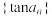 的通项公式;
的通项公式;
(2)求正整数 ,使得
,使得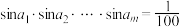 .
.
 满足
满足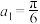 ,
,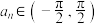 ,
,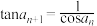 ,
,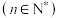 .
.(1)证明:数列
 为等差数列,并求数列
为等差数列,并求数列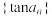 的通项公式;
的通项公式;(2)求正整数
 ,使得
,使得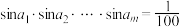 .
.
您最近一年使用:0次
2024-05-03更新
|
1544次组卷
|
4卷引用:江西省八所重点中学2024届高三下学期4月联考数学试卷
江西省八所重点中学2024届高三下学期4月联考数学试卷江西省八所重点中学2024届高三下学期4月联考数学试卷重庆市第一中学校2023-2024学年高二下学期期中考试数学试题(已下线)第一章数列章末综合检测卷(新题型)-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)
3 . 已知数列 中
中 ,
,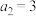 ,且满足
,且满足 .设
.设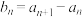 ,
, .
.
(1)证明数列 是等比数列;
是等比数列;
(2)求数列 的前n项和
的前n项和 .
.
 中
中 ,
,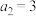 ,且满足
,且满足 .设
.设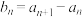 ,
, .
.(1)证明数列
 是等比数列;
是等比数列;(2)求数列
 的前n项和
的前n项和 .
.
您最近一年使用:0次
名校
4 . 若数列 满足
满足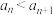 ,从数列
,从数列 中任取2项相加,把所有和的不同值按照从小到大排成一列,称为数列
中任取2项相加,把所有和的不同值按照从小到大排成一列,称为数列 的和数列,记作数列
的和数列,记作数列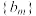 .
.
(1)已知等差数列 的前n项和为
的前n项和为 ,且
,且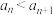 .
.
①若 ,
, ,求
,求 的通项公式,并写出
的通项公式,并写出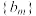 的前5项;
的前5项;
②若 ,
, ,求数列
,求数列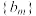 的前50项的和;
的前50项的和;
(2)若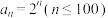 ,证明:对任意
,证明:对任意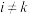 或
或 ,
,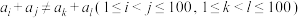 ,并求数列
,并求数列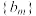 的所有项的和.
的所有项的和.
 满足
满足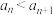 ,从数列
,从数列 中任取2项相加,把所有和的不同值按照从小到大排成一列,称为数列
中任取2项相加,把所有和的不同值按照从小到大排成一列,称为数列 的和数列,记作数列
的和数列,记作数列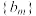 .
.(1)已知等差数列
 的前n项和为
的前n项和为 ,且
,且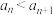 .
.①若
 ,
, ,求
,求 的通项公式,并写出
的通项公式,并写出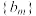 的前5项;
的前5项;②若
 ,
, ,求数列
,求数列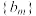 的前50项的和;
的前50项的和;(2)若
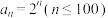 ,证明:对任意
,证明:对任意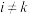 或
或 ,
,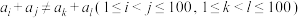 ,并求数列
,并求数列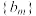 的所有项的和.
的所有项的和.
您最近一年使用:0次
2024-04-30更新
|
110次组卷
|
3卷引用:江西省抚州市金溪县第一中学等校2023-2024学年高二下学期期中考试数学试卷
5 . 已知数列 的前
的前 项和为
项和为 ,且
,且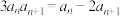 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记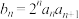 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
 的前
的前 项和为
项和为 ,且
,且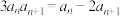 .
.(1)求数列
 的通项公式;
的通项公式;(2)记
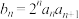 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
您最近一年使用:0次
6 . 在 个数码
个数码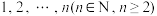 构成的一个排列
构成的一个排列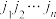 中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如
中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如 ,则
,则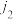 与
与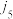 构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为
构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为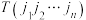 ,例如,
,例如,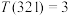 .
.
(1)计算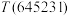 ;
;
(2)设数列 满足
满足 ,
, ,求
,求 的通项公式;
的通项公式;
(3)设排列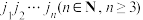 满足
满足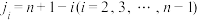 ,
, ,
, ,
,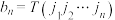 ,
,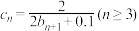 ,证明:
,证明: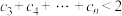 .
.
 个数码
个数码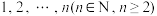 构成的一个排列
构成的一个排列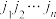 中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如
中,若一个较大的数码排在一个较小的数码的前面,则称它们构成逆序(例如 ,则
,则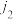 与
与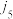 构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为
构成逆序),这个排列的所有逆序的总个数称为这个排列的逆序数,记为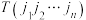 ,例如,
,例如,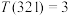 .
.(1)计算
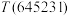 ;
;(2)设数列
 满足
满足 ,
, ,求
,求 的通项公式;
的通项公式;(3)设排列
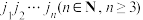 满足
满足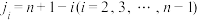 ,
, ,
, ,
,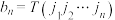 ,
,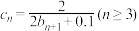 ,证明:
,证明: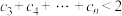 .
.
您最近一年使用:0次
名校
解题方法
7 . 在 中,
中,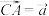 ,
,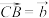 ,若
,若 是
是 的中点
的中点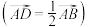 ,则
,则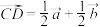 ;若
;若 是
是 的一个三等分点
的一个三等分点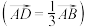 ,则
,则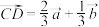 ;若
;若 是
是 的一个四等分点
的一个四等分点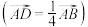 ,则
,则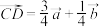
 ,用
,用 ,
, 表示
表示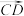 ,你能得出什么结论?并加以证明.
,你能得出什么结论?并加以证明.
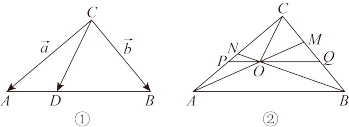
(2)如图②,若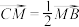 ,
, ,
, 与
与 交于
交于 ,过
,过 点的直线
点的直线 与
与 ,
, 分别交于点
分别交于点 ,
, .
.
①利用(1)的结论,用 ,
, 表示
表示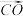 ;
;
②设 ,
,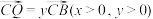 ,求
,求 的最小值.
的最小值.
 中,
中,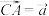 ,
,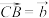 ,若
,若 是
是 的中点
的中点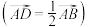 ,则
,则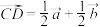 ;若
;若 是
是 的一个三等分点
的一个三等分点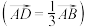 ,则
,则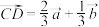 ;若
;若 是
是 的一个四等分点
的一个四等分点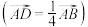 ,则
,则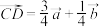
 ,用
,用 ,
, 表示
表示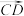 ,你能得出什么结论?并加以证明.
,你能得出什么结论?并加以证明.(2)如图②,若
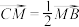 ,
, ,
, 与
与 交于
交于 ,过
,过 点的直线
点的直线 与
与 ,
, 分别交于点
分别交于点 ,
, .
.①利用(1)的结论,用
 ,
, 表示
表示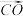 ;
;②设
 ,
,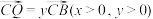 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-04-24更新
|
379次组卷
|
3卷引用:江西省南昌市第十中学2023-2024学年高一下学期第二次月考数学试题
江西省南昌市第十中学2023-2024学年高一下学期第二次月考数学试题广东实验中学2023-2024学年高一下学期第一次段考数学试题(已下线)第1题 向量的线性运算和平面向量基本定理(高一期末每日一题)
名校
解题方法
8 . 已知圆C的方程为: ,直线l的方程为:
,直线l的方程为: ,
,
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)证明:直线l与圆C相交,设直线l与圆C相交于A、B,求弦长 的最小值,及此时直线l的方程;
的最小值,及此时直线l的方程;
(3)圆C的圆心C与A、B构成三角形,求三角形ABC面积的最大值.
 ,直线l的方程为:
,直线l的方程为: ,
,(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)证明:直线l与圆C相交,设直线l与圆C相交于A、B,求弦长
 的最小值,及此时直线l的方程;
的最小值,及此时直线l的方程;(3)圆C的圆心C与A、B构成三角形,求三角形ABC面积的最大值.
您最近一年使用:0次
2024-04-07更新
|
310次组卷
|
2卷引用:江西省宜春市宜丰中学2023-2024学年高二下学期3月月考数学试题
名校
解题方法
9 . 已知 为公差不为0的等差数列
为公差不为0的等差数列 的前
的前 项和,且
项和,且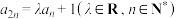 .
.
(1)求 的值;
的值;
(2)若 ,求证:
,求证: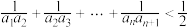 .
.
 为公差不为0的等差数列
为公差不为0的等差数列 的前
的前 项和,且
项和,且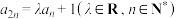 .
.(1)求
 的值;
的值;(2)若
 ,求证:
,求证: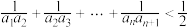 .
.
您最近一年使用:0次
2024-03-08更新
|
2295次组卷
|
7卷引用:江西省宜春市丰城市第九中学2023-2024学年高二下学期第一次月考数学试题
解题方法
10 . 对于数列 ,若满足
,若满足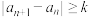 恒成立的最大正数
恒成立的最大正数 为
为 ,则称
,则称 为“
为“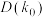 数列”.
数列”.
(1)已知等比数列 的首项为1,公比为
的首项为1,公比为 ,且为“
,且为“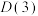 数列”,求
数列”,求 ;
;
(2)已知等差数列 与其前
与其前 项和
项和 均为“
均为“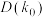 数列”,且
数列”,且 与
与 的单调性一致,求
的单调性一致,求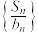 的通项公式;
的通项公式;
(3)已知数列 满足
满足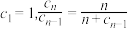 ,若
,若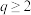 且
且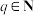 ,证明:存在实数
,证明:存在实数 ,使得
,使得 是“
是“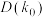 数列”,并求
数列”,并求 的最小值.
的最小值.
 ,若满足
,若满足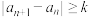 恒成立的最大正数
恒成立的最大正数 为
为 ,则称
,则称 为“
为“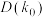 数列”.
数列”.(1)已知等比数列
 的首项为1,公比为
的首项为1,公比为 ,且为“
,且为“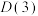 数列”,求
数列”,求 ;
;(2)已知等差数列
 与其前
与其前 项和
项和 均为“
均为“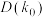 数列”,且
数列”,且 与
与 的单调性一致,求
的单调性一致,求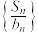 的通项公式;
的通项公式;(3)已知数列
 满足
满足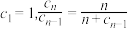 ,若
,若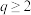 且
且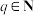 ,证明:存在实数
,证明:存在实数 ,使得
,使得 是“
是“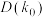 数列”,并求
数列”,并求 的最小值.
的最小值.
您最近一年使用:0次
2024-03-21更新
|
138次组卷
|
2卷引用:江西省部分学校2023-2024学年高二下学期第一次阶段性考试数学试卷



