1 . 已知函数 有唯一的零点,则实数
有唯一的零点,则实数 的值可以是
的值可以是__________ .【写出一个符合要求的值即可】
 有唯一的零点,则实数
有唯一的零点,则实数 的值可以是
的值可以是
您最近一年使用:0次
名校
2 . 已知函数 ,若在平面直角坐标系
,若在平面直角坐标系 中,所有满足
中,所有满足 的点
的点 都不在直线
都不在直线 上,则直线
上,则直线 的方程可以是
的方程可以是__________ (写出满足条件的一个直线方程即可).
 ,若在平面直角坐标系
,若在平面直角坐标系 中,所有满足
中,所有满足 的点
的点 都不在直线
都不在直线 上,则直线
上,则直线 的方程可以是
的方程可以是
您最近一年使用:0次
名校
3 . 函数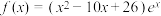 ,若
,若 ,
, ,
, ,都有
,都有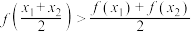 成立,则满足条件的一个区间
成立,则满足条件的一个区间 可以是
可以是__________ (填写一个符合题意的区间即可).
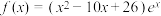 ,若
,若 ,
, ,
, ,都有
,都有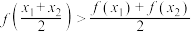 成立,则满足条件的一个区间
成立,则满足条件的一个区间 可以是
可以是
您最近一年使用:0次
2021-05-12更新
|
982次组卷
|
5卷引用:模块五 专题5 全真拔高模拟5
解题方法
4 . 对于 个复数
个复数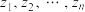 ,如果存在
,如果存在 个不全为零的实数
个不全为零的实数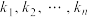 ,使得
,使得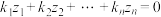 ,就称
,就称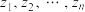 线性相关.若要说明复数
线性相关.若要说明复数 ,
,
 线性相关,则可取
线性相关,则可取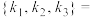
________ .(只要写出满足条件的一组值即可)
 个复数
个复数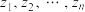 ,如果存在
,如果存在 个不全为零的实数
个不全为零的实数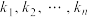 ,使得
,使得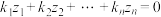 ,就称
,就称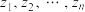 线性相关.若要说明复数
线性相关.若要说明复数 ,
,
 线性相关,则可取
线性相关,则可取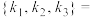
您最近一年使用:0次
名校
解题方法
5 . 易拉罐用料最省问题的研究.小明同学最近注意到一条新闻,易拉罐(如图所示)作为饮品的容器,每年的用量可达数万亿个.这让他想到一个用料最优化的问题,即在易拉罐的体积(容积)一定的情况下,如何确定易拉罐的高和半径才能使得用料最省?他研究发现易拉罐的上盖、下底和侧壁的厚度是不同的,进而结合数学建模知识进行了深入研究.以下是小明的研究过程,请回答其中问题.
(1)建立模型问题1: 填空:记圆柱容积为 ,高为
,高为 ,底面半径为
,底面半径为 , 则
, 则 ___________; ①记上盖、下底和侧壁的厚度分别为
___________; ①记上盖、下底和侧壁的厚度分别为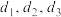 (底面半径都为
(底面半径都为 ),且侧壁展开可看成长方体(长、宽、高分别为
),且侧壁展开可看成长方体(长、宽、高分别为 ),金属用料总量为C(接口材料忽略不计),则
),金属用料总量为C(接口材料忽略不计),则 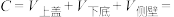 ___________ ;②因为
___________ ;②因为 都是常数,不妨设
都是常数,不妨设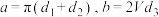 ,则由① ②可得用料总量的函数可简化为
,则由① ②可得用料总量的函数可简化为 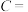 _____________(用
_____________(用 表示) ③;
表示) ③;
(2)求解模型:问题2:求解当 取何值时(用
取何值时(用 表示),
表示), 取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知
取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知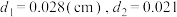
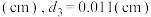 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得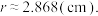 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
(3)模型评价与改进:问题3:模型计算结果与现实数据存在较大差异的原因可能为_________相应改进措施为__________.
注:只需一条原因及相应改进措施即可

(1)建立模型问题1: 填空:记圆柱容积为
 ,高为
,高为 ,底面半径为
,底面半径为 , 则
, 则 ___________; ①记上盖、下底和侧壁的厚度分别为
___________; ①记上盖、下底和侧壁的厚度分别为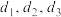 (底面半径都为
(底面半径都为 ),且侧壁展开可看成长方体(长、宽、高分别为
),且侧壁展开可看成长方体(长、宽、高分别为 ),金属用料总量为C(接口材料忽略不计),则
),金属用料总量为C(接口材料忽略不计),则 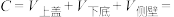 ___________ ;②因为
___________ ;②因为 都是常数,不妨设
都是常数,不妨设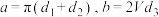 ,则由① ②可得用料总量的函数可简化为
,则由① ②可得用料总量的函数可简化为 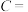 _____________(用
_____________(用 表示) ③;
表示) ③;(2)求解模型:问题2:求解当
 取何值时(用
取何值时(用 表示),
表示), 取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知
取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知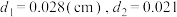
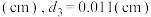 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得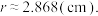 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;(3)模型评价与改进:问题3:模型计算结果与现实数据存在较大差异的原因可能为_________相应改进措施为__________.
注:只需一条原因及相应改进措施即可
您最近一年使用:0次
解题方法
6 . 已知定义城为 的函数
的函数 同时具有下列三个性质,则
同时具有下列三个性质,则
__________ .(写出一个满足条件的函数即可)
①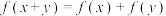 ;②
;② 是偶函数;③当
是偶函数;③当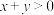 时,
时,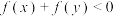 .
.
 的函数
的函数 同时具有下列三个性质,则
同时具有下列三个性质,则
①
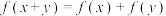 ;②
;② 是偶函数;③当
是偶函数;③当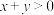 时,
时,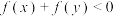 .
.
您最近一年使用:0次
解题方法
7 . 已知函数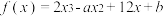 在
在 处取得极小值,且
处取得极小值,且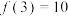 ,若
,若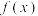 值域为
值域为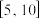 ,则其定义域可以为
,则其定义域可以为_____________ .(写出一个符合条件的即可)
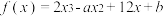 在
在 处取得极小值,且
处取得极小值,且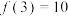 ,若
,若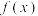 值域为
值域为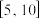 ,则其定义域可以为
,则其定义域可以为
您最近一年使用:0次
解题方法
8 . “当 时,函数
时,函数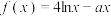 在区间
在区间 上单调递增”为真命题的
上单调递增”为真命题的 的一个取值是
的一个取值是__________ .(写出符合题意的一个值即可)
 时,函数
时,函数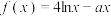 在区间
在区间 上单调递增”为真命题的
上单调递增”为真命题的 的一个取值是
的一个取值是
您最近一年使用:0次
2023-12-11更新
|
254次组卷
|
4卷引用:江苏省南京市励志高级中学2023-2024学年高二上学期期末模拟数学试题
江苏省南京市励志高级中学2023-2024学年高二上学期期末模拟数学试题(已下线)模块五 专题1 全真基础模拟1宁夏银川市贺兰县景博中学2021-2022学年高二上学期期末考试数学(文)试题(已下线)专题09 利用导数研究函数的单调性(九大题型+过关检测专训)-2023-2024学年高二数学《重难点题型·高分突破》(人教A版2019选择性必修第二册)
9 . 阅读以下材料,判断下列命题的真假
在复数域内,大小成为了没有意义的量,那么我们能否赋予它一个定义呢.在实数域内,我们通常用绝对值来描述大小,而复数域中也相应的有复数的模长来代替绝对值,于是,我们只需定义复数的正负即可.我们规定复数的“长度”即为模长,规定在复平面x轴上方的复数为正,在x轴下方的复数为负,在x轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用[z]来表示这个复数的“大小”
例如 ,
,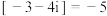 ,
,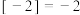 ,
,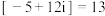 .
.
①在复平面上的复数的大小一定大于在它正下方的复数大小;
②在复平面内做一条直线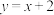 ,
, 对应的点在该直线上,则
对应的点在该直线上,则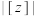 的最小值为
的最小值为 ;
;
③复数 ;
;
④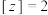 在复平面上表现为一个半圆;
在复平面上表现为一个半圆;
⑤无法在复平面上找到满足方程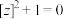 的点.
的点.
其中,正确的序号为__________
在复数域内,大小成为了没有意义的量,那么我们能否赋予它一个定义呢.在实数域内,我们通常用绝对值来描述大小,而复数域中也相应的有复数的模长来代替绝对值,于是,我们只需定义复数的正负即可.我们规定复数的“长度”即为模长,规定在复平面x轴上方的复数为正,在x轴下方的复数为负,在x轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用[z]来表示这个复数的“大小”
例如
 ,
,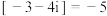 ,
,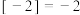 ,
,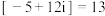 .
.①在复平面上的复数的大小一定大于在它正下方的复数大小;
②在复平面内做一条直线
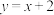 ,
, 对应的点在该直线上,则
对应的点在该直线上,则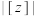 的最小值为
的最小值为 ;
;③复数
 ;
;④
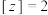 在复平面上表现为一个半圆;
在复平面上表现为一个半圆;⑤无法在复平面上找到满足方程
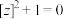 的点.
的点.其中,正确的序号为
您最近一年使用:0次
10 . 在复数城内,大小成为了没有意义的量,那么我们能否赋予它一个定义呢,在实数域内,我们通常用绝对值来描述大小,而复数域中也相应的有复数的模长来代替绝对值,于是,我们只需定义复数的正负即可,我们规定复数的“长度”即为模长,规定在复平面x轴上方的复数为正,在x轴下方的复数为负,在x轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用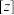 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: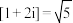 ,
, ,
, ,
, ,
,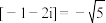 ,则下列说法正确的是( )
,则下列说法正确的是( )
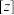 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: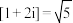 ,
, ,
, ,
, ,
,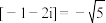 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 在复平面内表示一个圆 在复平面内表示一个圆 |
B.若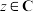 ,则方程 ,则方程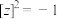 无解 无解 |
C.若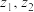 为虚数,且 为虚数,且 ,则 ,则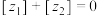 |
D.复平面内,复数 对应的点在直线 对应的点在直线 上,则 上,则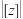 最小值为 最小值为 |
您最近一年使用:0次



