解题方法
1 . 求所有的 ,使
,使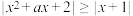 对
对 恒成立.
恒成立.
 ,使
,使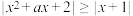 对
对 恒成立.
恒成立.
您最近一年使用:0次
2024-04-13更新
|
320次组卷
|
2卷引用:2024年中国科学技术大学创新班营(一)数学考试真题
解题方法
2 . 已知函数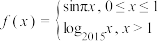 ,若
,若 互不相等,且
互不相等,且 ,则
,则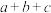 的取值范围是( ).
的取值范围是( ).
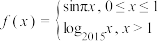 ,若
,若 互不相等,且
互不相等,且 ,则
,则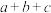 的取值范围是( ).
的取值范围是( ).A.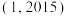 | B.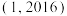 |
C.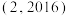 | D.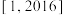 |
您最近一年使用:0次
3 . 已知定义在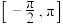 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当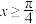 时,
时, .
.
(1)求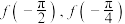 的值;
的值;
(2)求 的函数表达式;
的函数表达式;
(3)如果关于 的方程
的方程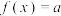 有解,记
有解,记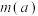 为方程所有解的和,求
为方程所有解的和,求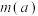 .
.
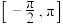 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当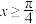 时,
时, .
.(1)求
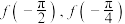 的值;
的值;(2)求
 的函数表达式;
的函数表达式;(3)如果关于
 的方程
的方程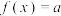 有解,记
有解,记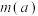 为方程所有解的和,求
为方程所有解的和,求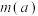 .
.
您最近一年使用:0次
解题方法
4 . 已知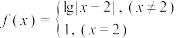 若关于
若关于 的方程
的方程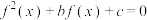 恰有3个不同的实数解
恰有3个不同的实数解 ,则
,则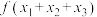 等于( ).
等于( ).
| A.0 | B. | C.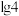 | D.1 |
您最近一年使用:0次
解题方法
5 . 已知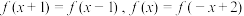 ,方程
,方程 在
在 内有且只有一个根
内有且只有一个根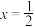 ,则
,则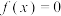 在区间
在区间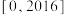 内根的个数为( )
内根的个数为( )
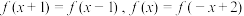 ,方程
,方程 在
在 内有且只有一个根
内有且只有一个根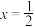 ,则
,则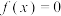 在区间
在区间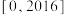 内根的个数为( )
内根的个数为( )| A.2013 | B.1008 | C.2016 | D.1009 |
您最近一年使用:0次
解题方法
6 . 已知函数 .数列
.数列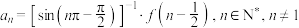 .
.
(1)请判断方程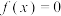 在区间
在区间 上的根的个数,并说明理由;
上的根的个数,并说明理由;
(2) 是否是轴对称函数,如果是,求出对称轴;若不是,说明理由;
是否是轴对称函数,如果是,求出对称轴;若不是,说明理由;
(3)求证: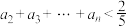 .
.
 .数列
.数列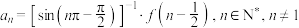 .
.(1)请判断方程
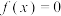 在区间
在区间 上的根的个数,并说明理由;
上的根的个数,并说明理由;(2)
 是否是轴对称函数,如果是,求出对称轴;若不是,说明理由;
是否是轴对称函数,如果是,求出对称轴;若不是,说明理由;(3)求证:
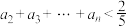 .
.
您最近一年使用:0次
解题方法
7 . 方程 (
( 且
且 )的解的个数为
)的解的个数为______ 个.
 (
( 且
且 )的解的个数为
)的解的个数为
您最近一年使用:0次
解题方法
8 . 对于函数 ,设
,设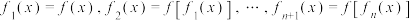 ,令
,令 ,则集合
,则集合 中的元素个数为( )
中的元素个数为( )
 ,设
,设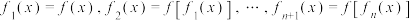 ,令
,令 ,则集合
,则集合 中的元素个数为( )
中的元素个数为( )| A.0个 | B.1个 | C.2个 | D.3个 |
您最近一年使用:0次
解题方法
9 . 已知函数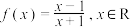 且
且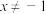 .
.
(1)就 的取值情况,讨论关于
的取值情况,讨论关于 的方程
的方程 在
在 上的解的个数;
上的解的个数;
(2)若可变动的实数 满足
满足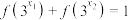 ,求
,求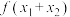 的最小值.
的最小值.
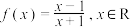 且
且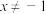 .
.(1)就
 的取值情况,讨论关于
的取值情况,讨论关于 的方程
的方程 在
在 上的解的个数;
上的解的个数;(2)若可变动的实数
 满足
满足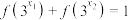 ,求
,求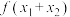 的最小值.
的最小值.
您最近一年使用:0次
10 . 已知 是函数
是函数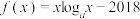 的一个零点,
的一个零点, 是函数
是函数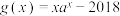 的一个零点,则
的一个零点,则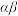 的值为( ).
的值为( ).
 是函数
是函数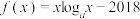 的一个零点,
的一个零点, 是函数
是函数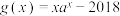 的一个零点,则
的一个零点,则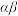 的值为( ).
的值为( ).| A.1 | B.2018 | C.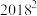 | D.4036 |
您最近一年使用:0次



