1 . 已知函数 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足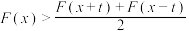 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.
(1)试判断函数 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);
(2)若函数 具有“性质
具有“性质 ”,且
”,且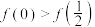 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;
(3)若函数 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,
①若 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;
②若 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足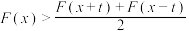 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.(1)试判断函数
 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);(2)若函数
 具有“性质
具有“性质 ”,且
”,且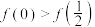 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;(3)若函数
 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,①若
 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;②若
 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
您最近一年使用:0次
2023-01-12更新
|
615次组卷
|
6卷引用:专题10 指数及指数函数压轴题-【常考压轴题】
(已下线)专题10 指数及指数函数压轴题-【常考压轴题】(已下线)第五章 函数的概念、性质及应用(压轴必刷30题9种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(10个考点专练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】(人教A版2019必修第一册)上海市闵行区2022-2023学年高一上学期期末数学试题(已下线)第四章 指数函数与对数函数-【优化数学】单元测试能力卷(人教A版2019)
21-22高一·湖南·课后作业
解题方法
2 . 证明不等式:
(1)若 ,
, ,
, ,
, 都是正数,求证:
都是正数,求证: ;
;
(2)若 ,
, ,
, 是非负实数,则
是非负实数,则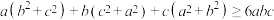 ;
;
(3)若 ,
, 是非负实数,则
是非负实数,则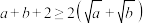 ;
;
(4)若 ,
,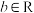 ,则
,则 .
.
(1)若
 ,
, ,
, ,
, 都是正数,求证:
都是正数,求证: ;
;(2)若
 ,
, ,
, 是非负实数,则
是非负实数,则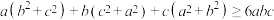 ;
;(3)若
 ,
, 是非负实数,则
是非负实数,则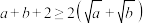 ;
;(4)若
 ,
,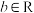 ,则
,则 .
.
您最近一年使用:0次
名校
3 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴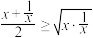 ,即
,即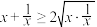 ,∴
,∴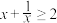 ,
,
当且仅当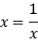 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①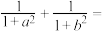 ___________.
___________.
②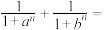 ___________.
___________.
(2)若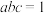 ,解方程
,解方程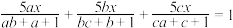 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴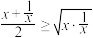 ,即
,即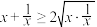 ,∴
,∴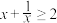 ,
,当且仅当
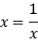 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
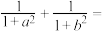 ___________.
___________.②
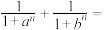 ___________.
___________.(2)若
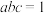 ,解方程
,解方程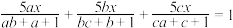 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2021-10-29更新
|
525次组卷
|
3卷引用:第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)江苏省南通中学2020-2021学年高一上学期开学考试数学试题江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)
解题方法
4 . (1)设x,y为正数,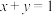 ,证明
,证明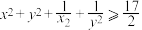 ;
;
(2)x,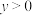 ,
,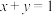 ,求证:对于任意正整数n,
,求证:对于任意正整数n,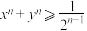 .
.
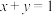 ,证明
,证明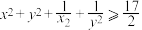 ;
;(2)x,
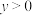 ,
,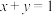 ,求证:对于任意正整数n,
,求证:对于任意正整数n,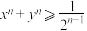 .
.
您最近一年使用:0次
2022高三·全国·专题练习
解题方法
5 . (1)已知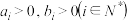 ,比较
,比较 与
与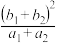 的大小,试将其推广至一般性结论并证明;
的大小,试将其推广至一般性结论并证明;
(2)求证: .
.
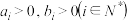 ,比较
,比较 与
与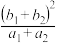 的大小,试将其推广至一般性结论并证明;
的大小,试将其推广至一般性结论并证明;(2)求证:
 .
.
您最近一年使用:0次
名校
6 . 函数的凹凸性的定义是由丹麦著名的数学家兼工程师Johan Jensen在1905年提出来的.其中对于凸函数的定义如下:设连续函数 的定义域为
的定义域为 (或开区间
(或开区间 或
或 ,或
,或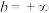 都可以),若对于区间
都可以),若对于区间 上任意两个数
上任意两个数 ,均有
,均有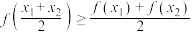 成立,则称
成立,则称 为区间
为区间 上的凸函数.容易证明譬如
上的凸函数.容易证明譬如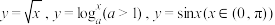 都是凸函数.Johan Jensen在1906年将上述不等式推广到了
都是凸函数.Johan Jensen在1906年将上述不等式推广到了 个变量的情形,即著名的Jensen不等式:若函数
个变量的情形,即著名的Jensen不等式:若函数 为其定义域上的凸函数,则对其定义域内任意
为其定义域上的凸函数,则对其定义域内任意 个数
个数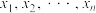 ,均有
,均有 成立,当且仅当
成立,当且仅当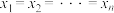 时等号成立.
时等号成立.
(1)若函数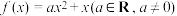 为
为 上的凸函数,求
上的凸函数,求 的取值范围:
的取值范围:
(2)在 中,求
中,求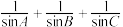 的最小值;
的最小值;
(3)若连续函数 的定义域和值域都是
的定义域和值域都是 ,且对于任意
,且对于任意 均满足下述两个不等式:
均满足下述两个不等式: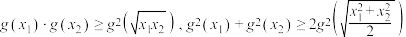 ,证明:函数
,证明:函数 为
为 上的凸函数.(注:
上的凸函数.(注: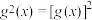 )
)
 的定义域为
的定义域为 (或开区间
(或开区间 或
或 ,或
,或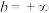 都可以),若对于区间
都可以),若对于区间 上任意两个数
上任意两个数 ,均有
,均有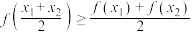 成立,则称
成立,则称 为区间
为区间 上的凸函数.容易证明譬如
上的凸函数.容易证明譬如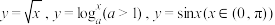 都是凸函数.Johan Jensen在1906年将上述不等式推广到了
都是凸函数.Johan Jensen在1906年将上述不等式推广到了 个变量的情形,即著名的Jensen不等式:若函数
个变量的情形,即著名的Jensen不等式:若函数 为其定义域上的凸函数,则对其定义域内任意
为其定义域上的凸函数,则对其定义域内任意 个数
个数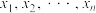 ,均有
,均有 成立,当且仅当
成立,当且仅当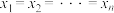 时等号成立.
时等号成立.(1)若函数
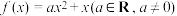 为
为 上的凸函数,求
上的凸函数,求 的取值范围:
的取值范围:(2)在
 中,求
中,求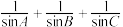 的最小值;
的最小值;(3)若连续函数
 的定义域和值域都是
的定义域和值域都是 ,且对于任意
,且对于任意 均满足下述两个不等式:
均满足下述两个不等式: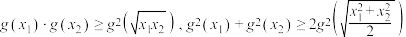 ,证明:函数
,证明:函数 为
为 上的凸函数.(注:
上的凸函数.(注: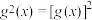 )
)
您最近一年使用:0次
解题方法
7 . 某乡镇为全面实施乡村振兴战略,大力发展特色农产业,提升特色农产品的知名度,邀请了一家广告牌制作公司设计一个宽为x米、长为y米的长方形展牌,其中 ,并要求其面积为
,并要求其面积为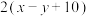 平方米.
平方米.
(1)求y关于x的函数 ;
;
(2)判断 在其定义域内的单调性,并用定义证明;
在其定义域内的单调性,并用定义证明;
(3)如何设计展牌的长和宽,才能使展牌的周长最小?
 ,并要求其面积为
,并要求其面积为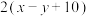 平方米.
平方米.(1)求y关于x的函数
 ;
;(2)判断
 在其定义域内的单调性,并用定义证明;
在其定义域内的单调性,并用定义证明;(3)如何设计展牌的长和宽,才能使展牌的周长最小?
您最近一年使用:0次
2023-12-15更新
|
293次组卷
|
3卷引用:3.4函数的应用(一)【第二练】“上好三节课,做好三套题“高中数学素养晋级之路
(已下线)3.4函数的应用(一)【第二练】“上好三节课,做好三套题“高中数学素养晋级之路河南省八地市2023-2024学年高一上学期期中联考数学试题河南省2023-2024学年高一上学期学业质量监测考试数学试题(濮阳、周口版)
8 . 已知函数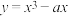 (
( 为常数)的图象上存在四个点
为常数)的图象上存在四个点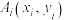 ,过
,过 的切线为
的切线为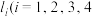 ,其中
,其中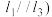 ,且
,且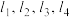 围成的图形是正方形.
围成的图形是正方形.
(1)求证: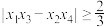 ;
;
(2)试求 的取值范围.
的取值范围.
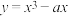 (
( 为常数)的图象上存在四个点
为常数)的图象上存在四个点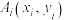 ,过
,过 的切线为
的切线为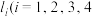 ,其中
,其中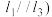 ,且
,且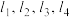 围成的图形是正方形.
围成的图形是正方形.(1)求证:
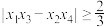 ;
;(2)试求
 的取值范围.
的取值范围.
您最近一年使用:0次
名校
9 . 根据多元微分求条件极值理论,要求二元函数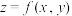 在约束条件
在约束条件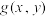 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数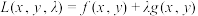 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对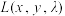 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下:
 ,解此方程组,得出解
,解此方程组,得出解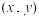 ,就是二元函数
,就是二元函数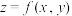 在约束条件
在约束条件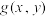 的可能极值点.
的可能极值点. 的值代入到
的值代入到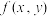 中即为极值.
中即为极值.
补充说明:【例】求函数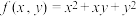 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的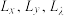 表示分别对
表示分别对 进行求导.
进行求导.
(1)求函数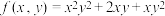 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.
(2)利用拉格朗日乘数法求:设实数 满足
满足 ,求
,求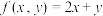 的最大值.
的最大值.
(3)①若 为实数,且
为实数,且 ,证明:
,证明: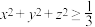 .
.
②设 ,求
,求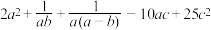 的最小值.
的最小值.
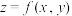 在约束条件
在约束条件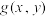 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数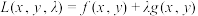 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对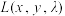 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下: ,解此方程组,得出解
,解此方程组,得出解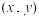 ,就是二元函数
,就是二元函数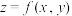 在约束条件
在约束条件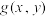 的可能极值点.
的可能极值点. 的值代入到
的值代入到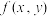 中即为极值.
中即为极值.补充说明:【例】求函数
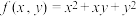 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的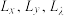 表示分别对
表示分别对 进行求导.
进行求导.(1)求函数
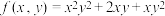 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.(2)利用拉格朗日乘数法求:设实数
 满足
满足 ,求
,求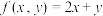 的最大值.
的最大值.(3)①若
 为实数,且
为实数,且 ,证明:
,证明: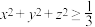 .
.②设
 ,求
,求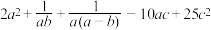 的最小值.
的最小值.
您最近一年使用:0次
解题方法
10 . 在四面体 中,
中, 为
为 中点,
中点, 为
为 外接球的球心,
外接球的球心,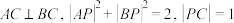 .
.
(1)证明: ;
;
(2)若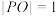 ,求四面体
,求四面体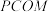 体积的最大值.
体积的最大值.
 中,
中, 为
为 中点,
中点, 为
为 外接球的球心,
外接球的球心,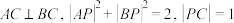 .
.(1)证明:
 ;
;(2)若
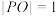 ,求四面体
,求四面体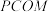 体积的最大值.
体积的最大值.
您最近一年使用:0次



