名校
解题方法
1 . 在平面直角坐标系 中,已知双曲线
中,已知双曲线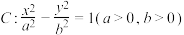 的右焦点为
的右焦点为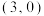 ,且经过点
,且经过点 .
. 的标准方程;
的标准方程;
(2)已知 ,
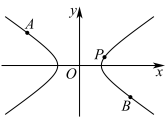
, 是双曲线
是双曲线 上关于原点对称的两点,垂直于
上关于原点对称的两点,垂直于 的直线
的直线 与双曲线
与双曲线 相切于点
相切于点 ,当点
,当点 位于第一象限,且
位于第一象限,且 被
被 轴分割为面积比为
轴分割为面积比为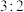 的两部分时,求直线
的两部分时,求直线 的方程.
的方程.
 中,已知双曲线
中,已知双曲线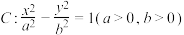 的右焦点为
的右焦点为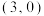 ,且经过点
,且经过点 .
.
 的标准方程;
的标准方程;(2)已知
 ,
, 是双曲线
是双曲线 上关于原点对称的两点,垂直于
上关于原点对称的两点,垂直于 的直线
的直线 与双曲线
与双曲线 相切于点
相切于点 ,当点
,当点 位于第一象限,且
位于第一象限,且 被
被 轴分割为面积比为
轴分割为面积比为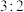 的两部分时,求直线
的两部分时,求直线 的方程.
的方程.
您最近一年使用:0次
2023-12-10更新
|
516次组卷
|
10卷引用:江苏省南京市2021-2022学年高二上学期期中数学试题
江苏省南京市2021-2022学年高二上学期期中数学试题(已下线)一轮复习大题专练66—双曲线2—2022届高三数学一轮复习福建省厦门双十中学2023届高三上学期期中考试数学试题江苏省扬州大学附属中学2022-2023学年高二上学期期中数学试题广西师范大学附属中学2022-2023学年高二上学期11月期中考试数学试题安徽省合肥市肥东县综合高中2022-2023学年高二下学期第一次月考(2月)数学试题江苏省徐州高级中学2023-2024学年高二上学期期中考试数学试卷(已下线)专题12双曲线(3个知识点5个拓展2个突破8种题型5个易错点)-【倍速学习法】2023-2024学年高二数学核心知识点与常见题型通关讲解练(人教A版2019选修第一册)(已下线)专题18 圆锥曲线高频压轴解答题(16大核心考点)(讲义)-1吉林省吉林市第一中学2022-2023学年高二上学期11月考试数学试题(平行班)
2 . 已知 的面积为
的面积为 ,且
,且 ,其中O为坐标原点.
,其中O为坐标原点.
(1)设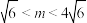 ,求
,求 与
与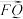 的夹角
的夹角 的正切值的取值范围;
的正切值的取值范围;
(2)设以O为中心,F在x轴正半轴上,且F为右焦点的双曲线经过点Q, ,
,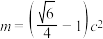 ,当
,当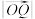 取得最小值时,求此双曲线的标准方程.
取得最小值时,求此双曲线的标准方程.
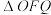 的面积为
的面积为 ,且
,且 ,其中O为坐标原点.
,其中O为坐标原点.(1)设
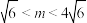 ,求
,求 与
与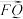 的夹角
的夹角 的正切值的取值范围;
的正切值的取值范围;(2)设以O为中心,F在x轴正半轴上,且F为右焦点的双曲线经过点Q,
 ,
,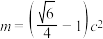 ,当
,当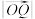 取得最小值时,求此双曲线的标准方程.
取得最小值时,求此双曲线的标准方程.
您最近一年使用:0次
2023-05-30更新
|
87次组卷
|
3卷引用:2.2.1双曲线及其标准方程 课时作业2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册
解题方法
3 . 已知双曲线E的两个焦点分别为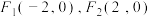 ,并且E经过点
,并且E经过点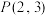 .
.
(1)求双曲线E的方程;
(2)过点 的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
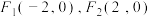 ,并且E经过点
,并且E经过点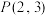 .
.(1)求双曲线E的方程;
(2)过点
 的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
您最近一年使用:0次
2023-08-24更新
|
1018次组卷
|
16卷引用:专题07 圆锥曲线的方程-双曲线的综合运用-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)
(已下线)专题07 圆锥曲线的方程-双曲线的综合运用-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)人教A版(2019) 选修第一册 实战演练 第三章 课时练习26 直线与双曲线的位置关系福建省漳州市2019-2020学年高二上学期期末数学试题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 专题强化练7 双曲线的综合运用河南省周口市太康县第三高级中学2022-2023学年高二上学期12月月考理数试题河南省周口市太康县第三高级中学2022-2023学年高二上学期12月月考文数试题新疆维吾尔自治区昌吉回族自治州2022-2023学年高二上学期11月期中质量检测数学试题(已下线)考点巩固卷21 双曲线方程及其性质(十一大考点)(已下线)考点15 直线与圆锥曲线相切问题 2024届高考数学考点总动员辽宁省沈阳市东北育才外国语学校2023-2024学年高二上学期期中教学诊断数学试题(已下线)第05讲 拓展二:直线与双曲线的位置关系(1)(已下线)3.2.2 双曲线的几何性质(1)(已下线)通关练16 双曲线13考点精练(100题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)专题3.2 双曲线(5个考点十大题型)(2)【课后练】 3.2.2 双曲线的简单几何性质 课后作业-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程(已下线)重组8 高二期中真题重组卷(辽宁卷)A基础卷
名校
4 . 求下列各曲线的标准方程:
(1)焦点在 轴上,焦距为
轴上,焦距为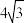 ,短轴长为4的椭圆;
,短轴长为4的椭圆;
(2)一个焦点为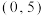 ,实轴长为6的双曲线.
,实轴长为6的双曲线.
(1)焦点在
 轴上,焦距为
轴上,焦距为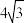 ,短轴长为4的椭圆;
,短轴长为4的椭圆;(2)一个焦点为
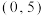 ,实轴长为6的双曲线.
,实轴长为6的双曲线.
您最近一年使用:0次
2023-03-27更新
|
1306次组卷
|
3卷引用:陕西省渭南市合阳县第二高级中学2021-2022学年高二上学期第二次月考文科数学试题
陕西省渭南市合阳县第二高级中学2021-2022学年高二上学期第二次月考文科数学试题(已下线)2.2.2 双曲线的简单几何性质(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)江西省九江市永修县第一中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
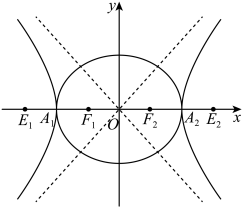
5 . 如图,椭圆 、双曲线
、双曲线 中心为坐标原点
中心为坐标原点 ,焦点在
,焦点在 轴上,且有相同的顶点
轴上,且有相同的顶点 ,
, ,
, 的焦点为
的焦点为 ,
, ,
, 的焦点为
的焦点为 ,
,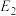 ,点
,点 ,
, ,
, ,
, ,
, 恰为线段
恰为线段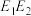 的六等分点,我们把
的六等分点,我们把 和
和 合成为曲线
合成为曲线 ,已知
,已知 的长轴长为4.
的长轴长为4.
(1)求曲线 的方程;
的方程;
(2)若 为
为 上一动点,
上一动点, 为定点,求
为定点,求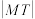 的最小值;
的最小值;
(3)若直线 过点
过点 ,与
,与 交于
交于 ,
, 两点,与
两点,与 交于
交于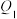 ,
, 两点,点
两点,点 、
、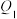 位于同一象限,且直线
位于同一象限,且直线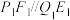 ,求直线
,求直线 的方程.
的方程.
 、双曲线
、双曲线 中心为坐标原点
中心为坐标原点 ,焦点在
,焦点在 轴上,且有相同的顶点
轴上,且有相同的顶点 ,
, ,
, 的焦点为
的焦点为 ,
, ,
, 的焦点为
的焦点为 ,
,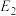 ,点
,点 ,
, ,
, ,
, ,
, 恰为线段
恰为线段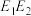 的六等分点,我们把
的六等分点,我们把 和
和 合成为曲线
合成为曲线 ,已知
,已知 的长轴长为4.
的长轴长为4.
(1)求曲线
 的方程;
的方程;(2)若
 为
为 上一动点,
上一动点, 为定点,求
为定点,求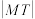 的最小值;
的最小值;(3)若直线
 过点
过点 ,与
,与 交于
交于 ,
, 两点,与
两点,与 交于
交于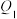 ,
, 两点,点
两点,点 、
、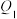 位于同一象限,且直线
位于同一象限,且直线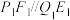 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2023-02-09更新
|
695次组卷
|
4卷引用:上海市七宝中学2021届高三下学期6月高考模拟数学试题
名校
6 . 已知点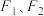 为双曲线
为双曲线 的左右焦点,过
的左右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线于点
轴上方交双曲线于点 ,且
,且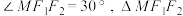 的面积为
的面积为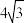 .圆
.圆 的方程是
的方程是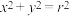 .
.
(1)求双曲线的方程;
(2)过双曲线上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 ,求
,求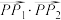 的值;
的值;
(3)过圆 上任意一点
上任意一点 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于 两点,
两点, 中点为
中点为 ,若
,若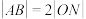 恒成立,试确定圆
恒成立,试确定圆 半径
半径 .
.
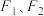 为双曲线
为双曲线 的左右焦点,过
的左右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线于点
轴上方交双曲线于点 ,且
,且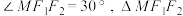 的面积为
的面积为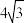 .圆
.圆 的方程是
的方程是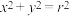 .
.(1)求双曲线的方程;
(2)过双曲线上任意一点
 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 ,求
,求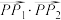 的值;
的值;(3)过圆
 上任意一点
上任意一点 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于 两点,
两点, 中点为
中点为 ,若
,若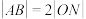 恒成立,试确定圆
恒成立,试确定圆 半径
半径 .
.
您最近一年使用:0次
2023-02-08更新
|
764次组卷
|
4卷引用:上海市交通大学附属中学2022届高三上学期期末数学试题
上海市交通大学附属中学2022届高三上学期期末数学试题(已下线)专题10 圆锥曲线综合大题10种题型归类-【寒假分层作业】2024年高二数学寒假培优练(人教A版2019选择性必修第一册)上海市奉贤区奉贤中学2024届高三下学期开学考试数学试题(已下线)专题7-4圆锥曲线五个方程型大题归类-2
名校
解题方法
7 . 求满足下列条件的曲线的方程:
(1)离心率为 ,长轴长为8且焦点在x轴的椭圆的标准方程;
,长轴长为8且焦点在x轴的椭圆的标准方程;
(2)与椭圆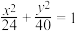 有相同焦点,且经过点
有相同焦点,且经过点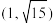 的双曲线的标准方程.
的双曲线的标准方程.
(1)离心率为
 ,长轴长为8且焦点在x轴的椭圆的标准方程;
,长轴长为8且焦点在x轴的椭圆的标准方程;(2)与椭圆
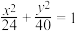 有相同焦点,且经过点
有相同焦点,且经过点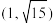 的双曲线的标准方程.
的双曲线的标准方程.
您最近一年使用:0次
名校
解题方法
8 . 双曲线 的左、右焦点分别为
的左、右焦点分别为 、
、 ,直线
,直线 过
过 且与双曲线交于
且与双曲线交于 两点.
两点.
(1)若 的倾斜角为
的倾斜角为 ,
,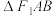 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设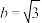 ,
, 点是线段
点是线段 中点,且
中点,且 ,若
,若 的斜率存在,求
的斜率存在,求 的斜率.
的斜率.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,直线
,直线 过
过 且与双曲线交于
且与双曲线交于 两点.
两点.(1)若
 的倾斜角为
的倾斜角为 ,
,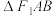 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;(2)设
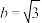 ,
, 点是线段
点是线段 中点,且
中点,且 ,若
,若 的斜率存在,求
的斜率存在,求 的斜率.
的斜率.
您最近一年使用:0次
名校
解题方法
9 . 设 、
、 分别为双曲线
分别为双曲线 的左、右顶点,双曲线的实轴长为4,焦点到渐近线的距离为1.
的左、右顶点,双曲线的实轴长为4,焦点到渐近线的距离为1.
(1)求双曲线的方程;
(2)已知椭圆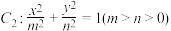 的焦点与双曲线
的焦点与双曲线 的左右顶点重合,且离心率为
的左右顶点重合,且离心率为 .直线
.直线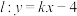 交椭圆
交椭圆 于
于 、
、 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
 、
、 分别为双曲线
分别为双曲线 的左、右顶点,双曲线的实轴长为4,焦点到渐近线的距离为1.
的左、右顶点,双曲线的实轴长为4,焦点到渐近线的距离为1.(1)求双曲线的方程;
(2)已知椭圆
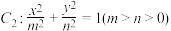 的焦点与双曲线
的焦点与双曲线 的左右顶点重合,且离心率为
的左右顶点重合,且离心率为 .直线
.直线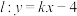 交椭圆
交椭圆 于
于 、
、 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线C的焦点、顶点恰好分别是椭圆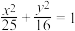 的长轴端点、焦点,求双曲线C的方程及其渐近线方程.
的长轴端点、焦点,求双曲线C的方程及其渐近线方程.
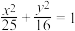 的长轴端点、焦点,求双曲线C的方程及其渐近线方程.
的长轴端点、焦点,求双曲线C的方程及其渐近线方程.
您最近一年使用:0次



