1 . 已知抛物线 :
: 的焦点
的焦点 ,直线
,直线 过
过 且交C于两点
且交C于两点 ,已知当
,已知当 时,
时, 中点纵坐标的值为
中点纵坐标的值为 .
.
(1)求 的标准方程.
的标准方程.
(2)令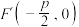 ,P为C上的一点,直线
,P为C上的一点,直线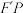 ,
,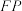 分别交C于另两点A,B.证明:
分别交C于另两点A,B.证明: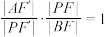 .
.
(3)过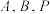 分别作
分别作 的切线
的切线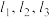 ,
, 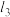 与
与 相交于
相交于 ,同时与
,同时与 相交于
相交于 ,求四边形
,求四边形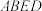 面积取值范围.
面积取值范围.
 :
: 的焦点
的焦点 ,直线
,直线 过
过 且交C于两点
且交C于两点 ,已知当
,已知当 时,
时, 中点纵坐标的值为
中点纵坐标的值为 .
.(1)求
 的标准方程.
的标准方程.(2)令
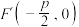 ,P为C上的一点,直线
,P为C上的一点,直线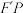 ,
,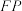 分别交C于另两点A,B.证明:
分别交C于另两点A,B.证明: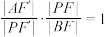 .
.(3)过
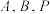 分别作
分别作 的切线
的切线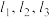 ,
, 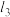 与
与 相交于
相交于 ,同时与
,同时与 相交于
相交于 ,求四边形
,求四边形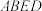 面积取值范围.
面积取值范围.
您最近半年使用:0次
2 . 过点 的直线与抛物线C:
的直线与抛物线C: 交于
交于 两点.抛物线
两点.抛物线 在点
在点 处的切线与直线
处的切线与直线 交于点
交于点 ,作
,作 交
交 于点
于点 ,则( )
,则( )
 的直线与抛物线C:
的直线与抛物线C: 交于
交于 两点.抛物线
两点.抛物线 在点
在点 处的切线与直线
处的切线与直线 交于点
交于点 ,作
,作 交
交 于点
于点 ,则( )
,则( )A.直线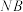 与抛物线C有2个公共点 与抛物线C有2个公共点 |
B.直线 恒过定点 恒过定点 |
C.点 的轨迹方程是 的轨迹方程是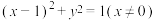 |
D.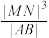 的最小值为 的最小值为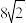 |
您最近半年使用:0次
解题方法
3 . 已知点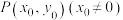 是抛物线
是抛物线 :
: 上一点,过点P作抛物线
上一点,过点P作抛物线 :
: 的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为
的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为 的焦点,则( )
的焦点,则( )
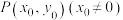 是抛物线
是抛物线 :
: 上一点,过点P作抛物线
上一点,过点P作抛物线 :
: 的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为
的两条切线PM,PN,切点分别为M,N,H为线段MN的中点,F为 的焦点,则( )
的焦点,则( )A.若 ,则直线MN经过点F ,则直线MN经过点F | B.直线 轴 轴 |
C.点H的轨迹方程为 | D. |
您最近半年使用:0次
名校
解题方法
4 . 设 为抛物线
为抛物线 的焦点,直线
的焦点,直线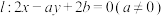 与
与 的准线
的准线 ,交于点
,交于点 .已知
.已知 与
与 相切,切点为
相切,切点为 ,直线
,直线 与
与 的一个交点为
的一个交点为 ,则( )
,则( )
 为抛物线
为抛物线 的焦点,直线
的焦点,直线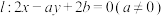 与
与 的准线
的准线 ,交于点
,交于点 .已知
.已知 与
与 相切,切点为
相切,切点为 ,直线
,直线 与
与 的一个交点为
的一个交点为 ,则( )
,则( )A.点 在 在 上 上 | B. |
C.以 为直径的圆与 为直径的圆与 相离 相离 | D.直线 与 与 相切 相切 |
您最近半年使用:0次
解题方法
5 . 如图,抛物线 在点
在点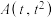 (
( )处的切线
)处的切线 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 (
( 的倾斜角与
的倾斜角与 的倾斜角互补)交抛物线于
的倾斜角互补)交抛物线于 ,
, 两点,求证:
两点,求证:
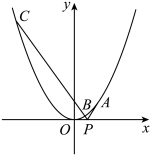
(1) 的斜率为
的斜率为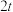 ;
;
(2)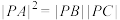 .
.
 在点
在点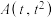 (
( )处的切线
)处的切线 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 (
( 的倾斜角与
的倾斜角与 的倾斜角互补)交抛物线于
的倾斜角互补)交抛物线于 ,
, 两点,求证:
两点,求证:
(1)
 的斜率为
的斜率为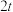 ;
;(2)
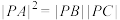 .
.
您最近半年使用:0次
解题方法
6 . 已知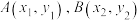 是抛物线
是抛物线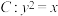 上不同于原点
上不同于原点 的两点,点
的两点,点 是抛物线
是抛物线 的焦点,下列说法正确的是( )
的焦点,下列说法正确的是( )
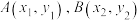 是抛物线
是抛物线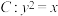 上不同于原点
上不同于原点 的两点,点
的两点,点 是抛物线
是抛物线 的焦点,下列说法正确的是( )
的焦点,下列说法正确的是( )A.点 的坐标为 的坐标为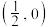 |
B. |
C.若 ,则直线 ,则直线 经过定点 经过定点 |
D.若点 为抛物线 为抛物线 的两条切线,则直线 的两条切线,则直线 的方程为 的方程为 |
您最近半年使用:0次
7 . 过直线 上一点
上一点 作拋物线
作拋物线 的两条切线,设切点分别为
的两条切线,设切点分别为 ,记
,记 是线段
是线段 的中点,则( )
的中点,则( )
 上一点
上一点 作拋物线
作拋物线 的两条切线,设切点分别为
的两条切线,设切点分别为 ,记
,记 是线段
是线段 的中点,则( )
的中点,则( )A.直线 经过该抛物线的焦点 经过该抛物线的焦点 |
B.直线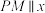 轴 轴 |
C.线段 的中点在该抛物线上 的中点在该抛物线上 |
D.以线段 为直径的圆与抛物线的准线相交 为直径的圆与抛物线的准线相交 |
您最近半年使用:0次
2023-02-12更新
|
675次组卷
|
4卷引用:浙江省绍兴市嵊州市2023届高三下学期2月学业质量调测数学试题
浙江省绍兴市嵊州市2023届高三下学期2月学业质量调测数学试题辽宁省本溪市高级中学2023-2024学年高三上学期高考适应性测试(一)数学试题江西省赣州市第四中学2024届高三上学期开学考试数学试题(已下线)考点20 常用的二级结论的应用 2024届高考数学考点总动员【练】
8 . 如图,过点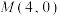 的直线l交抛物线
的直线l交抛物线 于A,B两点,O为坐标原点,点P是直线BO上的点,且
于A,B两点,O为坐标原点,点P是直线BO上的点,且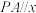 轴.
轴.
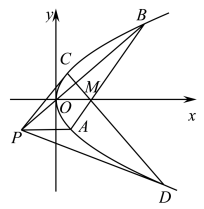
(1)当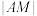 最小时,求直线l的方程;
最小时,求直线l的方程;
(2)若直线PC,PD分别与抛物线相切,切点是C,D,求证:C,M,D三点共线.
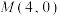 的直线l交抛物线
的直线l交抛物线 于A,B两点,O为坐标原点,点P是直线BO上的点,且
于A,B两点,O为坐标原点,点P是直线BO上的点,且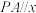 轴.
轴.
(1)当
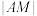 最小时,求直线l的方程;
最小时,求直线l的方程;(2)若直线PC,PD分别与抛物线相切,切点是C,D,求证:C,M,D三点共线.
您最近半年使用:0次
9 . 如图,过点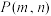 作抛物线
作抛物线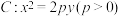 的两条切线
的两条切线 ,
, ,切点分别是
,切点分别是 ,
, ,动点
,动点 为抛物线
为抛物线 上在
上在 ,
, 之间部分上的任意一点,抛物线
之间部分上的任意一点,抛物线 在点
在点 处的切线分别交
处的切线分别交 ,
, 于点
于点 ,
, .
.
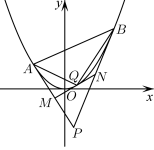
(1)若 ,证明:直线
,证明:直线 经过点
经过点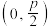 ;
;
(2)若分别记 ,
, 的面积为
的面积为 ,
, ,求
,求 的值.
的值.
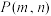 作抛物线
作抛物线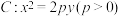 的两条切线
的两条切线 ,
, ,切点分别是
,切点分别是 ,
, ,动点
,动点 为抛物线
为抛物线 上在
上在 ,
, 之间部分上的任意一点,抛物线
之间部分上的任意一点,抛物线 在点
在点 处的切线分别交
处的切线分别交 ,
, 于点
于点 ,
, .
.
(1)若
 ,证明:直线
,证明:直线 经过点
经过点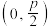 ;
;(2)若分别记
 ,
, 的面积为
的面积为 ,
, ,求
,求 的值.
的值.
您最近半年使用:0次
10 . 已知抛物线 :
: ,则使得
,则使得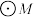 经过点
经过点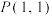 ,
,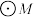 和抛物线
和抛物线 在
在 处的切线斜率相等,且
处的切线斜率相等,且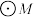 和坐标轴相切的点
和坐标轴相切的点 有( )
有( )
 :
: ,则使得
,则使得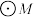 经过点
经过点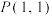 ,
,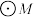 和抛物线
和抛物线 在
在 处的切线斜率相等,且
处的切线斜率相等,且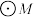 和坐标轴相切的点
和坐标轴相切的点 有( )
有( )| A.1个 | B.2个 | C.3个 | D.4个 |
您最近半年使用:0次



