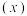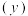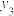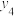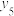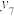1 . 发展新能源汽车是我国从汽车大国迈向汽车强国的必由之路,是应对气候变化推动绿色发展的战略举措.随着国务院《新能源汽车产业发展规划(2021—2035)》的发布,我国自主品牌汽车越来越具备竞争力.国产某品牌汽车对市场进行调研,统计了该品牌新能源汽车在某城市 年前几个月的销售量(单位:辆),用
年前几个月的销售量(单位:辆),用 表示第
表示第 月份该市汽车的销售量,得到如下统计表格:
月份该市汽车的销售量,得到如下统计表格:
(1)经研究, 、
、 满足线性相关关系,求
满足线性相关关系,求 关于
关于 的线性回归方程
的线性回归方程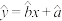 ,并根据此方程预测该店
,并根据此方程预测该店 月份的成交量(
月份的成交量( 、
、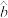 按四舍五入精确到整数);
按四舍五入精确到整数);
(2)该市某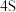 店为感谢客户,决定针对该品牌的汽车成交客户开展抽奖活动,设“一等奖”、“二等奖”和“祝您平安”三种奖项,“一等奖”奖励
店为感谢客户,决定针对该品牌的汽车成交客户开展抽奖活动,设“一等奖”、“二等奖”和“祝您平安”三种奖项,“一等奖”奖励 千元;“二等奖”奖励
千元;“二等奖”奖励 千元;“祝您平安”奖励纪念品一份.在一次抽奖活动中获得“二等奖”的概率为
千元;“祝您平安”奖励纪念品一份.在一次抽奖活动中获得“二等奖”的概率为 ,获得一份纪念品的概率为
,获得一份纪念品的概率为 ,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额 (千元)的分布列及数学期望.
(千元)的分布列及数学期望.
参考数据及公式: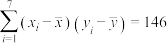 ,
,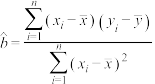 ,
,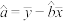 .
.
 年前几个月的销售量(单位:辆),用
年前几个月的销售量(单位:辆),用 表示第
表示第 月份该市汽车的销售量,得到如下统计表格:
月份该市汽车的销售量,得到如下统计表格:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 32 | 37 | 45 | 47 | 52 | 60 |
 、
、 满足线性相关关系,求
满足线性相关关系,求 关于
关于 的线性回归方程
的线性回归方程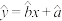 ,并根据此方程预测该店
,并根据此方程预测该店 月份的成交量(
月份的成交量( 、
、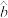 按四舍五入精确到整数);
按四舍五入精确到整数);(2)该市某
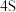 店为感谢客户,决定针对该品牌的汽车成交客户开展抽奖活动,设“一等奖”、“二等奖”和“祝您平安”三种奖项,“一等奖”奖励
店为感谢客户,决定针对该品牌的汽车成交客户开展抽奖活动,设“一等奖”、“二等奖”和“祝您平安”三种奖项,“一等奖”奖励 千元;“二等奖”奖励
千元;“二等奖”奖励 千元;“祝您平安”奖励纪念品一份.在一次抽奖活动中获得“二等奖”的概率为
千元;“祝您平安”奖励纪念品一份.在一次抽奖活动中获得“二等奖”的概率为 ,获得一份纪念品的概率为
,获得一份纪念品的概率为 ,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额 (千元)的分布列及数学期望.
(千元)的分布列及数学期望.参考数据及公式:
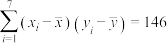 ,
,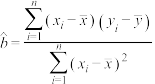 ,
,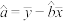 .
.
您最近一年使用:0次
2024-02-17更新
|
686次组卷
|
6卷引用:山东省日照市2023-2024学年高二上学期期末校际联合考试数学试题
山东省日照市2023-2024学年高二上学期期末校际联合考试数学试题2024届高三新改革适应性模拟训练数学试卷七(九省联考题型)(已下线)第八章 成对数据的统计分析(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)第9章 统计单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)专题02概率统计期末10种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019选择性必修第二册)(已下线)专题04 成对数据的统计分析-1
2 . 数字经济是继农业经济、工业经济之后的主要经济形态.近年来,在国家的大力推动下,我国数字经济规模增长迅猛,《“十四五”数字经济发展规划》更是将数字经济上升到了国家战略的层面.某地区2023年上半年月份 与对应数字经济的生产总值(即GDP)
与对应数字经济的生产总值(即GDP) (单位:亿元)如下表所示.
(单位:亿元)如下表所示.
根据上表可得到回归方程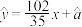 ,则( )
,则( )
 与对应数字经济的生产总值(即GDP)
与对应数字经济的生产总值(即GDP) (单位:亿元)如下表所示.
(单位:亿元)如下表所示.月份 | 1 | 2 | 3 | 4 | 5 | 6 |
生产总值 | 30 | 33 | 35 | 38 | 41 | 45 |
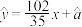 ,则( )
,则( )A. |
B. 与 与 正相关 正相关 |
C.若 表示变量 表示变量 与 与 之间的相关系数,则 之间的相关系数,则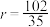 |
D.若该地区对数字经济的相关政策保持不变,则该地区7月份的生产总值约为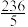 亿元 亿元 |
您最近一年使用:0次
3 . 某地政府为解除空巢老人日常护理和社会照料的困境,大力培育发展养老护理服务市场.从 年开始新建社区养老机构,下表为该地区近
年开始新建社区养老机构,下表为该地区近 年新建社区养老机构的数量对照表.
年新建社区养老机构的数量对照表.
(1)若该地区参与社区养老的老人的年龄 近似服从正态分布
近似服从正态分布 ,其中年龄
,其中年龄 的有
的有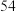 人,试估计该地参与社区养老的老人有多少?(结果按四舍五入取整数)
人,试估计该地参与社区养老的老人有多少?(结果按四舍五入取整数)
(2)已知变量 与
与 之间的样本相关系数
之间的样本相关系数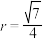 ,请求出
,请求出 关于
关于 的线性回归方程
的线性回归方程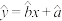 ,并据此估计
,并据此估计 年时,该地区新建社区养老机构的数量.(结果按四舍五入取整数)
年时,该地区新建社区养老机构的数量.(结果按四舍五入取整数)
参考公式与数据:①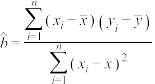 ,
,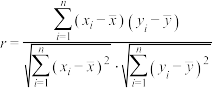 .;
.;
②若随机变量 ,则
,则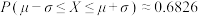 ,
, ,
,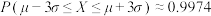 ;
;
③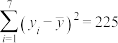 ,
,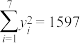 .
.
 年开始新建社区养老机构,下表为该地区近
年开始新建社区养老机构,下表为该地区近 年新建社区养老机构的数量对照表.
年新建社区养老机构的数量对照表.年份 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
新建社区养老机构 |
|
|
|
|
|
|
|
(1)若该地区参与社区养老的老人的年龄
 近似服从正态分布
近似服从正态分布 ,其中年龄
,其中年龄 的有
的有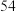 人,试估计该地参与社区养老的老人有多少?(结果按四舍五入取整数)
人,试估计该地参与社区养老的老人有多少?(结果按四舍五入取整数)(2)已知变量
 与
与 之间的样本相关系数
之间的样本相关系数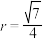 ,请求出
,请求出 关于
关于 的线性回归方程
的线性回归方程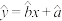 ,并据此估计
,并据此估计 年时,该地区新建社区养老机构的数量.(结果按四舍五入取整数)
年时,该地区新建社区养老机构的数量.(结果按四舍五入取整数)参考公式与数据:①
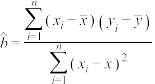 ,
,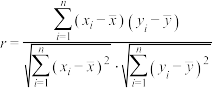 .;
.;②若随机变量
 ,则
,则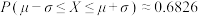 ,
, ,
,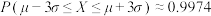 ;
;③
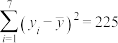 ,
,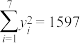 .
.
您最近一年使用:0次
解题方法
4 . 2023年9月23日—10月8日,亚运会在杭州举行,“碳中和”是本届亚运会一大亮点.为了打造碳中和亚运会,杭州亚运会上线了“亚运碳中和-减污降碳协同”数字化管理平台.该平台将数字化技术运用到碳排放采集、核算、减排、注销、评价管理全流程,探索建立了一套科学完整的碳排放管理体系.值此机会,某家公司重点推出新型品牌新能源汽车,以下是其中五个月的销售单:
(1)根据表中数据,求出 关于
关于 的线性回归方程;
的线性回归方程;
(2)随着亚运会的火热,新能源汽车也会一直持续下去,试估计2023年12月份该公司出售多少辆新能源汽车?
参考公式:对于一组具有线性相关关系的数据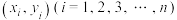 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为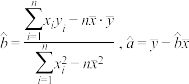 .
.
| 2023月份 | 5 | 6 | 7 | 8 | 9 |
月份代码 | 1 | 2 | 3 | 4 | 5 |
新能源车销售 (万辆) (万辆) | 1.6 | 2.1 | 2.7 | 3.7 | 4.6 |
 关于
关于 的线性回归方程;
的线性回归方程;(2)随着亚运会的火热,新能源汽车也会一直持续下去,试估计2023年12月份该公司出售多少辆新能源汽车?
参考公式:对于一组具有线性相关关系的数据
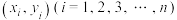 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为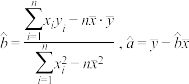 .
.
您最近一年使用:0次
名校
5 . 某学校研究性学习小组在学习生物遗传学的过程中,为验证高尔顿提出的关于儿子成年后身高 (单位:
(单位: )与父亲身高
)与父亲身高 (单位:
(单位: )之间的关系及存在的遗传规律,随机抽取了5对父子的身高数据,如下表:
)之间的关系及存在的遗传规律,随机抽取了5对父子的身高数据,如下表:
参考数据及公式: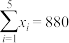 ,
,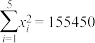 ,
, ,
,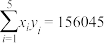 ,
,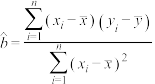 ,
, .
.
(1)根据表中数据,求出 关于
关于 的线性回归方程;
的线性回归方程;
(2)小明的父亲身高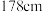 ,请你利用回归直线方程预测小明成年后的身高.
,请你利用回归直线方程预测小明成年后的身高.
 (单位:
(单位: )与父亲身高
)与父亲身高 (单位:
(单位: )之间的关系及存在的遗传规律,随机抽取了5对父子的身高数据,如下表:
)之间的关系及存在的遗传规律,随机抽取了5对父子的身高数据,如下表:父亲身高 | 160 | 170 | 175 | 185 | 190 |
儿子身高 | 170 | 174 | 175 | 180 | 186 |
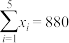 ,
,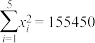 ,
, ,
,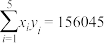 ,
,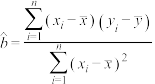 ,
, .
.(1)根据表中数据,求出
 关于
关于 的线性回归方程;
的线性回归方程;(2)小明的父亲身高
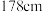 ,请你利用回归直线方程预测小明成年后的身高.
,请你利用回归直线方程预测小明成年后的身高.
您最近一年使用:0次
2024-01-30更新
|
393次组卷
|
2卷引用:四川省成都市石室中学2024届高三上学期期末数学(理)试题
解题方法
6 . 已知 与
与 具有相关关系,且利用
具有相关关系,且利用 关于
关于 的回归直线方程进行预测,当
的回归直线方程进行预测,当 时,
时,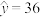 ,当
,当 时,
时, ,则
,则 关于
关于 的回归直线方程中的回归系数为
的回归直线方程中的回归系数为__________ .
 与
与 具有相关关系,且利用
具有相关关系,且利用 关于
关于 的回归直线方程进行预测,当
的回归直线方程进行预测,当 时,
时,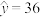 ,当
,当 时,
时, ,则
,则 关于
关于 的回归直线方程中的回归系数为
的回归直线方程中的回归系数为
您最近一年使用:0次
2024-01-17更新
|
217次组卷
|
3卷引用:辽宁省县级重点高中协作体2023-2024学年高二上学期期末数学试题
名校
7 . 5G技术在我国已经进入调整发展的阶段,5G手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:
若 与
与 线性相关,且线性回归方程为
线性相关,且线性回归方程为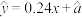 ,则下列说法不正确的是( )
,则下列说法不正确的是( )
时间 | 1 | 2 | 3 | 4 | 5 |
销售量 (千只) (千只) | 0.5 | 0.8 | 1.0 | 1.2 | 1.5 |
 与
与 线性相关,且线性回归方程为
线性相关,且线性回归方程为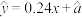 ,则下列说法不正确的是( )
,则下列说法不正确的是( )A.由题中数据可知,变量 与 与 正相关,且相关系数 正相关,且相关系数 |
B.线性回归方程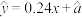 中 中 |
C.当解释变量 每增加1个单位时,预报变量 每增加1个单位时,预报变量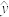 平均增加0.24个单位 平均增加0.24个单位 |
D.可以预测 时,该商场5G手机销量约为1.72(千只) 时,该商场5G手机销量约为1.72(千只) |
您最近一年使用:0次
名校
8 . 有人调查了某高校14名男大学生的身高及其父亲的身高,得到如下数据表:
利用最小二乘法计算的儿子身高 关于父亲身高
关于父亲身高 的回归直线为
的回归直线为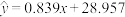 .
.
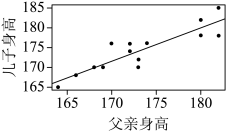
根据以上信息进行的如下推断中,正确的是( )
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
父亲身高/cm | 174 | 170 | 173 | 169 | 182 | 172 | 180 | 172 | 168 | 166 | 182 | 173 | 164 | 180 |
儿子身高/cm | 176 | 176 | 170 | 170 | 185 | 176 | 178 | 174 | 170 | 168 | 178 | 172 | 165 | 182 |
 关于父亲身高
关于父亲身高 的回归直线为
的回归直线为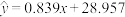 .
.
根据以上信息进行的如下推断中,正确的是( )
A.当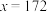 时, 时,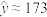 ,若一位父亲身高为 ,若一位父亲身高为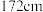 ,则他儿子长大成人后的身高一定是 ,则他儿子长大成人后的身高一定是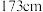 |
| B.父亲身高和儿子身高是正相关,因此身高更高的父亲,其儿子的身高也更高 |
| C.从回归直线中,无法判断父亲身高和儿子身高是正相关还是负相关 |
D.回归直线的斜率可以解释为父亲身高每增加 ,其儿子身高平均增加 ,其儿子身高平均增加 |
您最近一年使用:0次
名校
解题方法
9 . 某地区实行社会主义新农村建设后,农村的经济收入明显增加,根据统计得到从2015年至2021年农村居民家庭收入y(单位:万元)的数据,其数据如下表:
附:回归直线的斜率和截距的最小二乘估计公式分别为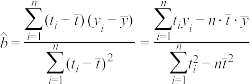 ,
, .
.
参考数据: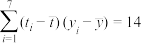 ,
,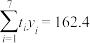 .
.
(1)求y关于t的线性回归方程;
(2)根据(1)中的回归方程,分析2015年至2021年该地区农村居民家庭收入的变化情况,并预测该地区2024年农村居民家庭收入.
年份 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
农村居民家庭收入y | 3.9 | 4.3 | 4.6 | 5.4 | 5.8 | 6.2 | 6.9 |
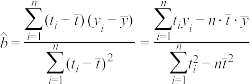 ,
, .
.参考数据:
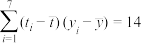 ,
,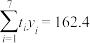 .
.(1)求y关于t的线性回归方程;
(2)根据(1)中的回归方程,分析2015年至2021年该地区农村居民家庭收入的变化情况,并预测该地区2024年农村居民家庭收入.
您最近一年使用:0次
2024-01-12更新
|
347次组卷
|
2卷引用:河南省焦作市第四中学2022-2023学年高二下学期4月月考数学试题
名校
10 . 研究表明,学生的学习成绩y(分)与每天投入的课后学习时间x(分钟)有较强的线性相关性.某校数学小组为了研究如何高效利用自己的学习时间,收集了该校高三(1)班学生9个月内在某学科(满分100分)所投入的课后学习时间和月考成绩的相关数据,下图是该小组制作的原始数据与统计图(散点图).

(1)当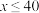 时,该小组建立了
时,该小组建立了 与
与 的线性回归模型,求其经验回归方程;
的线性回归模型,求其经验回归方程;
(2)当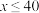 时,由图中观察到,第3个月的数据点明显偏离回归直线
时,由图中观察到,第3个月的数据点明显偏离回归直线 ,若剔除第3个月数据点后,用余下的4个散点做线性回归分析,得到新回归直线
,若剔除第3个月数据点后,用余下的4个散点做线性回归分析,得到新回归直线 ,证明:
,证明: ;
;
(3)当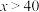 时,该小组确定了
时,该小组确定了 与
与 满足的线性回归方程为:
满足的线性回归方程为: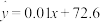 ,该数学小组建议该班在该学科投入课后学习时间为40分钟,请结合第(1)(2)问的结论说明该建议的合理性.
,该数学小组建议该班在该学科投入课后学习时间为40分钟,请结合第(1)(2)问的结论说明该建议的合理性.
附:经验回归直线的斜率和截距的最小二乘估计公式分别为: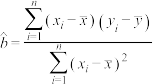 ,
,
| 月次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
某科课后投入时间 (分钟) (分钟) | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
高三(1)班某科平均分 (分) (分) | 65 | 68 | 75 | 72 | 73 | 73 | 73 | 73.5 | 73 |

(1)当
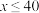 时,该小组建立了
时,该小组建立了 与
与 的线性回归模型,求其经验回归方程;
的线性回归模型,求其经验回归方程;(2)当
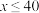 时,由图中观察到,第3个月的数据点明显偏离回归直线
时,由图中观察到,第3个月的数据点明显偏离回归直线 ,若剔除第3个月数据点后,用余下的4个散点做线性回归分析,得到新回归直线
,若剔除第3个月数据点后,用余下的4个散点做线性回归分析,得到新回归直线 ,证明:
,证明: ;
;(3)当
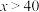 时,该小组确定了
时,该小组确定了 与
与 满足的线性回归方程为:
满足的线性回归方程为: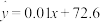 ,该数学小组建议该班在该学科投入课后学习时间为40分钟,请结合第(1)(2)问的结论说明该建议的合理性.
,该数学小组建议该班在该学科投入课后学习时间为40分钟,请结合第(1)(2)问的结论说明该建议的合理性.附:经验回归直线的斜率和截距的最小二乘估计公式分别为:
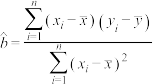 ,
,
您最近一年使用:0次