真题
名校
1 . 请先阅读:
在等式 (
( )的两边求导,得:
)的两边求导,得: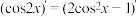 ,由求导法则,得
,由求导法则,得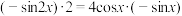 ,化简得等式:
,化简得等式: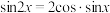 .
.
(1)利用上题的想法(或其他方法),结合等式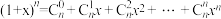 (
( ,正整数
,正整数 ),证明:
),证明: .
.
(2)对于正整数 ,求证:
,求证:
(i)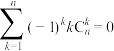 ; (ii)
; (ii)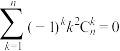 ; (iii)
; (iii) .
.
在等式
 (
( )的两边求导,得:
)的两边求导,得: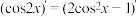 ,由求导法则,得
,由求导法则,得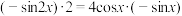 ,化简得等式:
,化简得等式: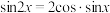 .
.(1)利用上题的想法(或其他方法),结合等式
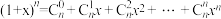 (
( ,正整数
,正整数 ),证明:
),证明: .
.(2)对于正整数
 ,求证:
,求证:(i)
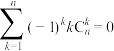 ; (ii)
; (ii)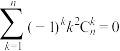 ; (iii)
; (iii) .
.
您最近一年使用:0次
2016-11-30更新
|
2398次组卷
|
4卷引用:2008年普通高等学校招生全国统一考试数学试题(江苏卷)
真题
解题方法
2 . A是由定义在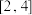 上且满足如下条件的函数
上且满足如下条件的函数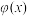 组成的集合:①对任意的
组成的集合:①对任意的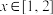 ,都有
,都有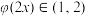 ;②存在常数
;②存在常数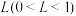 ,使得对任意的
,使得对任意的 ,都有
,都有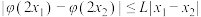 .
.
(1)设 ,证明:
,证明: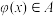 ;
;
(2)设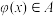 ,如果存在
,如果存在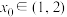 ,使得
,使得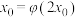 ,那么这样的
,那么这样的 是唯一的;
是唯一的;
(3)设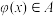 ,任取
,任取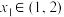 ,令
,令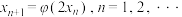 ,证明:给定正整数k,对任意的正整数p,不等式
,证明:给定正整数k,对任意的正整数p,不等式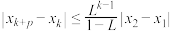 成立.
成立.
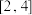 上且满足如下条件的函数
上且满足如下条件的函数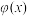 组成的集合:①对任意的
组成的集合:①对任意的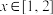 ,都有
,都有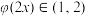 ;②存在常数
;②存在常数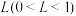 ,使得对任意的
,使得对任意的 ,都有
,都有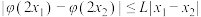 .
.(1)设
 ,证明:
,证明: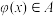 ;
;(2)设
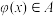 ,如果存在
,如果存在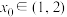 ,使得
,使得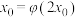 ,那么这样的
,那么这样的 是唯一的;
是唯一的;(3)设
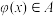 ,任取
,任取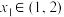 ,令
,令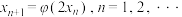 ,证明:给定正整数k,对任意的正整数p,不等式
,证明:给定正整数k,对任意的正整数p,不等式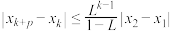 成立.
成立.
您最近一年使用:0次
真题
3 . 设 是定义在区间
是定义在区间 上的函数,且满足条件:
上的函数,且满足条件:
①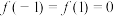 ;
;
②对任意的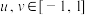 ,都有
,都有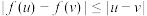 .
.
(1)证明:对任意的 ;
;
(2)判断函数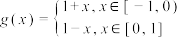 是否满足题设条件;
是否满足题设条件;
(3)在区间 上是否存在满足题设条件的函数
上是否存在满足题设条件的函数 ,且使得对任意的
,且使得对任意的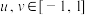 ,都有
,都有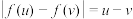 ,若存在,请举一例:若不存在,请说明理由.
,若存在,请举一例:若不存在,请说明理由.
 是定义在区间
是定义在区间 上的函数,且满足条件:
上的函数,且满足条件:①
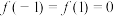 ;
;②对任意的
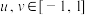 ,都有
,都有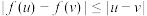 .
.(1)证明:对任意的
 ;
;(2)判断函数
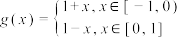 是否满足题设条件;
是否满足题设条件;(3)在区间
 上是否存在满足题设条件的函数
上是否存在满足题设条件的函数 ,且使得对任意的
,且使得对任意的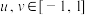 ,都有
,都有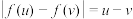 ,若存在,请举一例:若不存在,请说明理由.
,若存在,请举一例:若不存在,请说明理由.
您最近一年使用:0次
真题
解题方法
4 . 已知函数 .
.
(1)证明: 在
在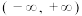 上是增函数;
上是增函数;
(2)证明:对于任意不小于3的自然数n,都有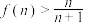 .
.
 .
.(1)证明:
 在
在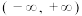 上是增函数;
上是增函数;(2)证明:对于任意不小于3的自然数n,都有
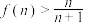 .
.
您最近一年使用:0次
5 . 在数列 中,若
中,若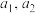 是正整数,且
是正整数,且 ,则称
,则称 为“绝对差数列”.
为“绝对差数列”.
(1)举出一个前五项不为零的“绝对差数列”(只要求写出前十项):
(2)若“绝对差数列” 中,
中,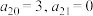 ,数列
,数列 满足
满足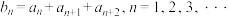 ,分别判断当
,分别判断当 时,
时, 与
与 的极限是否存在,如果存在,求出其极限值;
的极限是否存在,如果存在,求出其极限值;
(3)证明:任何“绝对差数列”中总含有无穷多个为零的项.
 中,若
中,若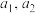 是正整数,且
是正整数,且 ,则称
,则称 为“绝对差数列”.
为“绝对差数列”.(1)举出一个前五项不为零的“绝对差数列”(只要求写出前十项):
(2)若“绝对差数列”
 中,
中,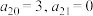 ,数列
,数列 满足
满足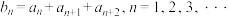 ,分别判断当
,分别判断当 时,
时, 与
与 的极限是否存在,如果存在,求出其极限值;
的极限是否存在,如果存在,求出其极限值;(3)证明:任何“绝对差数列”中总含有无穷多个为零的项.
您最近一年使用:0次
真题
6 . 给定实数a,且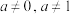 ,设函数
,设函数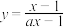 (
( 且
且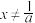 ).证明:
).证明:
(1)这个函数的图像上任意两个不同的点的直线不平行于 轴;
轴;
(2)这个函数的图像关于直线 成轴对称图形;
成轴对称图形;
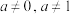 ,设函数
,设函数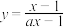 (
( 且
且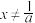 ).证明:
).证明:(1)这个函数的图像上任意两个不同的点的直线不平行于
 轴;
轴;(2)这个函数的图像关于直线
 成轴对称图形;
成轴对称图形;
您最近一年使用:0次
真题
7 . 设 是定义在区间
是定义在区间 上的函数,且满足条件:
上的函数,且满足条件:
①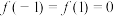 ;
;
②对任意的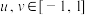 ,都有
,都有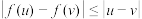 .
.
(1)证明:对任意的 ;
;
(2)证明:对任意的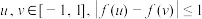 ;
;
(3)在区间 上是否存在满足题设条件的奇函数
上是否存在满足题设条件的奇函数 ;且使得
;且使得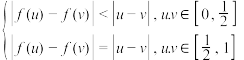 ,若存在,请举一例;若不存在,请说明理由.
,若存在,请举一例;若不存在,请说明理由.
 是定义在区间
是定义在区间 上的函数,且满足条件:
上的函数,且满足条件:①
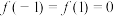 ;
;②对任意的
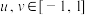 ,都有
,都有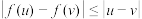 .
.(1)证明:对任意的
 ;
;(2)证明:对任意的
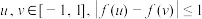 ;
;(3)在区间
 上是否存在满足题设条件的奇函数
上是否存在满足题设条件的奇函数 ;且使得
;且使得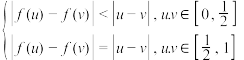 ,若存在,请举一例;若不存在,请说明理由.
,若存在,请举一例;若不存在,请说明理由.
您最近一年使用:0次
真题
名校
8 . 等差数列 的前
的前 项和为
项和为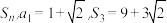 .
.
(Ⅰ)求数列 的通项
的通项 与前
与前 项和
项和 ;
;
(Ⅱ)设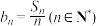 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
 的前
的前 项和为
项和为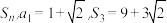 .
.(Ⅰ)求数列
 的通项
的通项 与前
与前 项和
项和 ;
;(Ⅱ)设
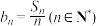 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
您最近一年使用:0次
2019-01-30更新
|
3393次组卷
|
27卷引用:2007年普通高等学校招生全国统一考试理科数学卷(福建)
2007年普通高等学校招生全国统一考试理科数学卷(福建)2007年普通高等学校招生考试数学(理)试题(福建卷)(已下线)2011届江西省师大附中高三上学期期中考试数学理卷(已下线)2011届江苏省无锡一中高三上学期期中考试数学试卷(已下线)2011届江苏省无锡市辅仁高级中学高三上学期期中数学卷(已下线)2012届山东省济宁市汶上一中高三11月月考理科数学试卷(已下线)2012届江西省吉水二中高三第四次月考理科数学试卷2015-2016学年贵州遵义航天高中高二3月考文科数学试卷2015-2016湖南常德石门一中高二下第一次月考文科数学卷2015-2016学年辽宁省鞍山一中高二下期中理科数学试卷高中数学人教A版选修2-2 第二章 推理与证明 2.2.2 反证法(2)湖北省部分重点中学2017-2018学年高二下学期期中考试数学(文)试题河南省南阳市2018-2019学年高二下学期期末考试数学(文)试题(已下线)专题11.2 直接证明与间接证明(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题11.5 第十一章 推理与证明、算法、复数(单元测试)(测)【文】-《2020年高考一轮复习讲练测》广东省华南师范大学附属中学2018-2019学年上学期高二年级期末数学试题(已下线)专题01 等差与等比数列的基本量的计算(第二篇)-备战2020年高考数学大题精做之解答题题型全覆盖沪教版(上海) 高三年级 新高考辅导与训练 第四章 数列与数学归纳法 一、等差数列与等比数列安徽省池州市第一中学2019-2020学年高二下学期期中教学质量检测数学(理)试题(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021届高考数学(文)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)考点57 推理与证明-备战2021年高考数学(理)一轮复习考点一遍过 (已下线)考点49 推理与证明-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点22 等差数列及其前n项和-备战2022年高考数学(理)一轮复习考点帮高中数学解题兵法 第一百讲 正难则反(已下线)专题6 等比数列的判断(证明)方法 微点1 定义法、等比中项法
真题
9 . 用反证法证明命题“设 为实数,则方程
为实数,则方程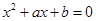 至少有一个实根”时,要做的假设是
至少有一个实根”时,要做的假设是
 为实数,则方程
为实数,则方程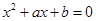 至少有一个实根”时,要做的假设是
至少有一个实根”时,要做的假设是A.方程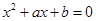 没有实根 没有实根 |
B.方程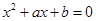 至多有一个实根 至多有一个实根 |
C.方程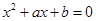 至多有两个实根 至多有两个实根 |
D.方程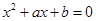 恰好有两个实根 恰好有两个实根 |
您最近一年使用:0次
2019-01-30更新
|
3943次组卷
|
11卷引用:2014年全国普通高等学校招生统一考试理科数学(山东卷)
2014年全国普通高等学校招生统一考试理科数学(山东卷)2014年全国普通高等学校招生统一考试文科数学(山东卷)2015-2016学年山西省怀仁一中高二11月月考文科数学卷2015-2016湖南常德石门一中高二下第一次月考文科数学卷2015-2016学年安徽师大附中高二下期中文科数学试卷2015-2016学年山东省济宁一中高二下期中理科数学试卷2015-2016学年山东省济宁一中高二下期中文科数学试卷2015-2016学年福建省泉州惠安荷山中学高二下期中理科数学试卷2015-2016学年吉林省长春十一中高二下期中文科数学试卷2015-2016学年山东省济宁市任城区高二下期中理科数学试卷山东省菏泽市2016-2017学年高二下学期期中考试数学(理)试题
真题
名校
10 . 设 和
和 是两个等差数列,记
是两个等差数列,记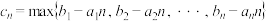
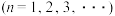 ,
,
其中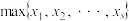 表示
表示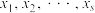 这
这 个数中最大的数.
个数中最大的数.
(Ⅰ)若 ,
, ,求
,求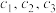 的值,并证明
的值,并证明 是等差数列;
是等差数列;
(Ⅱ)证明:或者对任意正数 ,存在正整数
,存在正整数 ,当
,当 时,
时,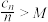 ;或者存在正整数
;或者存在正整数 ,使得
,使得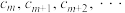 是等差数列.
是等差数列.
 和
和 是两个等差数列,记
是两个等差数列,记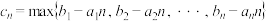
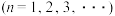 ,
,其中
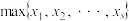 表示
表示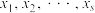 这
这 个数中最大的数.
个数中最大的数.(Ⅰ)若
 ,
, ,求
,求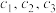 的值,并证明
的值,并证明 是等差数列;
是等差数列;(Ⅱ)证明:或者对任意正数
 ,存在正整数
,存在正整数 ,当
,当 时,
时,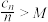 ;或者存在正整数
;或者存在正整数 ,使得
,使得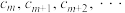 是等差数列.
是等差数列.
您最近一年使用:0次
2017-08-07更新
|
5386次组卷
|
19卷引用:2017年全国普通高等学校招生统一考试理科数学(北京卷精编版)
2017年全国普通高等学校招生统一考试理科数学(北京卷精编版)贵州省遵义市第四中学2017-2018学年高二上学期第一次月考数学试题(已下线)2018年高考二轮复习测试专项【苏教版】专题五 数列(已下线)专题12.2 直接证明与间接证明(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题11.2 直接证明与间接证明(练)【文】-《2020年高考一轮复习讲练测》北京市第五中学2019-2020学年高二下学期第一次段考数学试题(已下线)专题14 数列综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题33 算法、复数、推理与证明-十年(2011-2020)高考真题数学分项(八)(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)专题09 数列-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题12 盘点等差(比)数列的判断与证明——备战2022年高考数学二轮复习常考点专题突破北京市八一学校2022-2023学年高二下学期期中考试数学试题北京名校2023届高三二轮复习 专题三 集合与数列 第2讲 数列的综合应用(已下线)专题17 数列探索型、存在型问题的解法 微点2 数列存在型问题的解法北京市育英学校2022-2023学年高二下学期期中练习数学试题北京十年真题专题06数列北京市第一○一中学2022-2023学年高二下学期期中练习数学试题(已下线)专题21 数列解答题(理科)-4专题14数列



