1 . 国际象棋是国际通行的智力竞技运动.国际象棋使用 格黑白方格相间棋盘,骨牌为每格与棋盘的方格大小相同的
格黑白方格相间棋盘,骨牌为每格与棋盘的方格大小相同的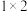 格灰色方格.若某种黑白相间棋盘与骨牌满足以下三点:①每块骨牌覆盖棋盘的相邻两格;②棋盘上每一格都被骨牌覆盖;③没有两块骨牌覆盖同一格,则称骨牌构成了棋盘的一种完全覆盖.显然,我们能够举例说明
格灰色方格.若某种黑白相间棋盘与骨牌满足以下三点:①每块骨牌覆盖棋盘的相邻两格;②棋盘上每一格都被骨牌覆盖;③没有两块骨牌覆盖同一格,则称骨牌构成了棋盘的一种完全覆盖.显然,我们能够举例说明 格黑白方格相间棋盘能被骨牌完全覆盖.
格黑白方格相间棋盘能被骨牌完全覆盖. 格黑白方格相间棋盘的对角两格,余下棋盘不能被骨牌完全覆盖;
格黑白方格相间棋盘的对角两格,余下棋盘不能被骨牌完全覆盖;
(2)请你切掉 格的黑白方格相间棋盘的任意两个异色方格,然后画出余下棋盘的一种骨牌完全覆盖方式,并证明:无论切掉的是哪两个异色方格,余下棋盘都能被骨牌完全覆盖;
格的黑白方格相间棋盘的任意两个异色方格,然后画出余下棋盘的一种骨牌完全覆盖方式,并证明:无论切掉的是哪两个异色方格,余下棋盘都能被骨牌完全覆盖;
(3)记 格黑白方格相间棋盘的骨牌完全覆盖方式数为
格黑白方格相间棋盘的骨牌完全覆盖方式数为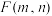 ,数列
,数列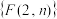 的前n项和为
的前n项和为 ,证明:
,证明: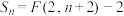 .
.
 格黑白方格相间棋盘,骨牌为每格与棋盘的方格大小相同的
格黑白方格相间棋盘,骨牌为每格与棋盘的方格大小相同的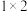 格灰色方格.若某种黑白相间棋盘与骨牌满足以下三点:①每块骨牌覆盖棋盘的相邻两格;②棋盘上每一格都被骨牌覆盖;③没有两块骨牌覆盖同一格,则称骨牌构成了棋盘的一种完全覆盖.显然,我们能够举例说明
格灰色方格.若某种黑白相间棋盘与骨牌满足以下三点:①每块骨牌覆盖棋盘的相邻两格;②棋盘上每一格都被骨牌覆盖;③没有两块骨牌覆盖同一格,则称骨牌构成了棋盘的一种完全覆盖.显然,我们能够举例说明 格黑白方格相间棋盘能被骨牌完全覆盖.
格黑白方格相间棋盘能被骨牌完全覆盖.
 格黑白方格相间棋盘的对角两格,余下棋盘不能被骨牌完全覆盖;
格黑白方格相间棋盘的对角两格,余下棋盘不能被骨牌完全覆盖;(2)请你切掉
 格的黑白方格相间棋盘的任意两个异色方格,然后画出余下棋盘的一种骨牌完全覆盖方式,并证明:无论切掉的是哪两个异色方格,余下棋盘都能被骨牌完全覆盖;
格的黑白方格相间棋盘的任意两个异色方格,然后画出余下棋盘的一种骨牌完全覆盖方式,并证明:无论切掉的是哪两个异色方格,余下棋盘都能被骨牌完全覆盖;(3)记
 格黑白方格相间棋盘的骨牌完全覆盖方式数为
格黑白方格相间棋盘的骨牌完全覆盖方式数为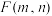 ,数列
,数列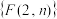 的前n项和为
的前n项和为 ,证明:
,证明: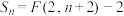 .
.
您最近一年使用:0次
2024-03-06更新
|
759次组卷
|
4卷引用:山东省菏泽第一中学人民路校区2024届高三下学期开学考试数学试题
山东省菏泽第一中学人民路校区2024届高三下学期开学考试数学试题(已下线)第四套 最新模拟重组卷江苏省苏州大学2024届高考新题型2月指导卷数学试题(已下线)压轴题08计数原理、二项式定理、概率统计压轴题6题型汇总
名校
解题方法
2 . 已知甲植物生长了一天,长度为 ,乙植物生长了一天,长度为
,乙植物生长了一天,长度为 .从第二天起,甲每天的生长速度是前一天的
.从第二天起,甲每天的生长速度是前一天的 倍,乙每天的生长速度是前一天的
倍,乙每天的生长速度是前一天的 ,则甲的长度第一次超过乙的长度的时期是( )(参考数据:取
,则甲的长度第一次超过乙的长度的时期是( )(参考数据:取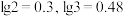 )
)
 ,乙植物生长了一天,长度为
,乙植物生长了一天,长度为 .从第二天起,甲每天的生长速度是前一天的
.从第二天起,甲每天的生长速度是前一天的 倍,乙每天的生长速度是前一天的
倍,乙每天的生长速度是前一天的 ,则甲的长度第一次超过乙的长度的时期是( )(参考数据:取
,则甲的长度第一次超过乙的长度的时期是( )(参考数据:取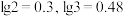 )
)| A.第6天 | B.第7天 | C.第8天 | D.第9天 |
您最近一年使用:0次
2024-02-27更新
|
890次组卷
|
7卷引用:山东省济南第一中学等校2024届高三下学期阶段性检测(开学考试)数学试题
名校
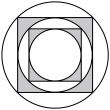
3 . 剪纸,又叫刻纸,是一种镂空艺术,是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下:取一张半径为1的圆形纸片,记为 ,在
,在 内作内接正方形,接着在该正方形内作内切圆,记为
内作内接正方形,接着在该正方形内作内切圆,记为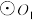 ,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操作,……重复上述裁剪操作n次,最终得到该剪纸.则第4次裁剪操作结束后所得
,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操作,……重复上述裁剪操作n次,最终得到该剪纸.则第4次裁剪操作结束后所得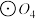 的面积为
的面积为______ ;第n次操作后,所有裁剪操作中裁剪去除的面积之和为______ .
 ,在
,在 内作内接正方形,接着在该正方形内作内切圆,记为
内作内接正方形,接着在该正方形内作内切圆,记为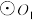 ,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操作,……重复上述裁剪操作n次,最终得到该剪纸.则第4次裁剪操作结束后所得
,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操作,……重复上述裁剪操作n次,最终得到该剪纸.则第4次裁剪操作结束后所得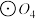 的面积为
的面积为
您最近一年使用:0次
2023-09-06更新
|
359次组卷
|
2卷引用:山东省临沂市2023-2024学年高三上学期开学摸底联考数学试题
名校
解题方法
4 . 欧拉是人类历史上最伟大的数学家之一.在数学史上,人们称18世纪为欧拉时代.直到今天,我们在数学及其应用的众多分支中,常常可以看到欧拉的名字,如著名的欧拉函数.欧拉函数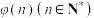 的函数值等于所有不超过正整数n且与n互素的正整数的个数,例如
的函数值等于所有不超过正整数n且与n互素的正整数的个数,例如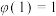 ,
,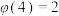 ,则下列说法正确的是( )
,则下列说法正确的是( )
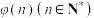 的函数值等于所有不超过正整数n且与n互素的正整数的个数,例如
的函数值等于所有不超过正整数n且与n互素的正整数的个数,例如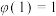 ,
,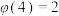 ,则下列说法正确的是( )
,则下列说法正确的是( )A. | B.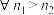 ,都有 ,都有 |
C.方程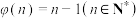 有无数个根 有无数个根 | D. |
您最近一年使用:0次
2023-08-05更新
|
411次组卷
|
3卷引用:山东省德州市第一中学2023-2024学年高三上学期开学测试数学试题
名校
5 . 已知有穷数列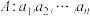
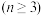 中的每一项都是不大于
中的每一项都是不大于 的正整数.对于满足
的正整数.对于满足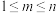 的整数
的整数 ,令集合
,令集合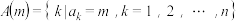 .记集合
.记集合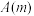 中元素的个数为
中元素的个数为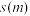 (约定空集的元素个数为0).
(约定空集的元素个数为0).
(1)若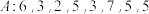 ,求
,求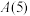 及
及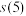 ;
;
(2)若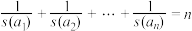 ,求证:
,求证: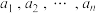 互不相同;
互不相同;
(3)已知 ,若对任意的正整数
,若对任意的正整数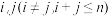 都有
都有 或
或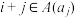 ,求
,求 的值.
的值.
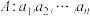
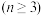 中的每一项都是不大于
中的每一项都是不大于 的正整数.对于满足
的正整数.对于满足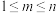 的整数
的整数 ,令集合
,令集合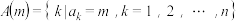 .记集合
.记集合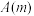 中元素的个数为
中元素的个数为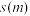 (约定空集的元素个数为0).
(约定空集的元素个数为0).(1)若
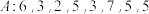 ,求
,求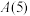 及
及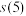 ;
;(2)若
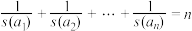 ,求证:
,求证: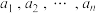 互不相同;
互不相同;(3)已知
 ,若对任意的正整数
,若对任意的正整数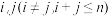 都有
都有 或
或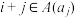 ,求
,求 的值.
的值.
您最近一年使用:0次
2023-05-05更新
|
3670次组卷
|
10卷引用:山东省实验中学2024届高三下学期2月调研考试数学试卷
名校
解题方法
6 . 克罗狄斯·托勒密是希腊数学家,他博学多才,既是天文学权威,也是地理学大师.托勒密定理是平面几何中非常著名的定理,它揭示了圆内接四边形的对角线与边长的内在联系,该定理的内容为圆的内接四边形中,两对角线长的乘积等于两组对边长乘积之和.已知四边形 是圆
是圆 的内接四边形,且
的内接四边形,且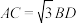 ,
,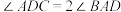 .若
.若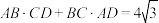 ,则圆
,则圆 的半径为( )
的半径为( )
 是圆
是圆 的内接四边形,且
的内接四边形,且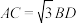 ,
,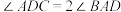 .若
.若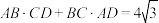 ,则圆
,则圆 的半径为( )
的半径为( )| A.4 | B.2 | C. | D. |
您最近一年使用:0次
2023-02-10更新
|
2026次组卷
|
8卷引用:山东省2022-2023学年高三下学期开学考试联考数学试题
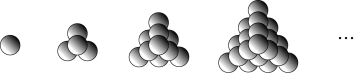
7 . 如图,用相同的球堆成若干堆“正三棱锥”形的装饰品,其中第1堆只有1层,且只有1个球;第2堆有2层,第1层有1个球,第2层有3个球;…;第堆有n层,第1层有1个球,第2层有3个球,第3层有6个球,……,第n层有 个球.记第n堆的球的总数为
个球.记第n堆的球的总数为 ,则(参考公式:
,则(参考公式: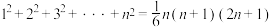 )( )
)( )
 个球.记第n堆的球的总数为
个球.记第n堆的球的总数为 ,则(参考公式:
,则(参考公式: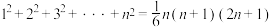 )( )
)( )
A.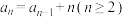 | B.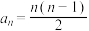 |
C. | D.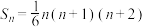 |
您最近一年使用:0次
2022-09-22更新
|
687次组卷
|
2卷引用:山东省济宁市汶上县第一中学2022-2023学年高三上学期第一次学业质量联合检测数学试题
8 . 已知等差数列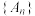 的首项
的首项 为
为 ,公差为
,公差为 ,在
,在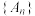 中每相邻两项之间都插入两个数,使它们和原数列的项一起构成一个新的等差数列
中每相邻两项之间都插入两个数,使它们和原数列的项一起构成一个新的等差数列 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若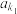 ,
,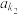 ,…,
,…,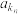 ,…是从
,…是从 中抽取的部分项按原来的顺序排列组成的一个等比数列,
中抽取的部分项按原来的顺序排列组成的一个等比数列, ,
, ,令
,令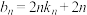 ,求数列
,求数列 的前
的前 项和
项和 .
.
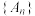 的首项
的首项 为
为 ,公差为
,公差为 ,在
,在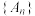 中每相邻两项之间都插入两个数,使它们和原数列的项一起构成一个新的等差数列
中每相邻两项之间都插入两个数,使它们和原数列的项一起构成一个新的等差数列 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
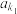 ,
,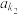 ,…,
,…,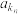 ,…是从
,…是从 中抽取的部分项按原来的顺序排列组成的一个等比数列,
中抽取的部分项按原来的顺序排列组成的一个等比数列, ,
, ,令
,令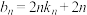 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2021-09-06更新
|
702次组卷
|
4卷引用:山东省青岛市2021-2022学年高三上学期开学考试数学试题
山东省青岛市2021-2022学年高三上学期开学考试数学试题山东省枣庄市滕州市第一中学2021-2022学年高三上学期10月月考数学试题山东省青岛市2021-2022学年高三上学期期初教学质量检测数学试题(已下线)江苏省南通市如皋市2022-2023学年高三上学期期初调研考前冲刺卷数学试题



