9-10高三·广西桂林·阶段练习
名校
1 . 设 ,则“
,则“ ”是“
”是“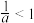 ”的( )
”的( )
 ,则“
,则“ ”是“
”是“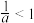 ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
7日内更新
|
771次组卷
|
293卷引用:2015-2016学年贵州省凯里一中高二下入学考试理科数学卷
2015-2016学年贵州省凯里一中高二下入学考试理科数学卷2015-2016学年贵州省凯里一中高二下入学考试文科数学卷贵州省黔东南州黎平县黎平三中2019-2020学年高二下学期期末考试数学(文)试题贵州省黔东南州黎平县黎平三中2019-2020学年高二下学期期末考试数学(理)试题贵州省黔西南州金成实验学校2022-2023学年高一上学期第一次月考数学试题(已下线)2011届广西壮族自治区桂林十八中高三第三次月考文科数学卷(已下线)2011届湖南省嘉积中学高二上学期质量检测数学理卷(已下线)2011年湖南省慈利一中高二上学期期末考试理科数学卷(已下线)2011年安徽省毫州市高二上学期期末考试数学理卷(已下线)2011年山西大学附中高二二月月考数学理卷(已下线)2011年广东省揭阳市第一中学高二上学期期末检测数学文卷(已下线)2011届浙江省宁波市十校高三联考数学文卷(已下线)2010-2011年浙江省瑞安中学高二下学期期中考试文科数学(已下线)2010-2011学年山东省临沂第一中学高二上学期学业水平测试数学试卷(已下线)2012届云南省昆明一中高三第一次月考理科数学(已下线)2012届云南省昆明一中高三上学期第一次月考试题文科数学(已下线)2012届甘肃省武威六中高三上学期期末考试理科数学试卷(已下线)2011-2012学年黑龙江省哈六中高二上学期期末理科数学试卷(已下线)2012届山东省临沂市苍山县高三上学期期末检测理科数学试卷(已下线)2011-2012学年河南省平顶山市高二下 期末调研考试理科数学试卷(已下线)2013届陕西省澄城县寺前中学高三第一次月考理科数学试卷(已下线)2013届浙江省绍兴一中分校高三10月学习质量诊断文科数学试卷(已下线)2013届山西省康杰中学等四校高三第一次联考理科数学试卷(已下线)2012-2013学年吉林省长春二中高二上学期期末考试文科数学试卷(已下线)2012-2013学年湖南省浏阳一中高二下学期第一次月考文科数学试卷(已下线)2013-2014学年河北邢台一中高二上学期第二次月考理数学试卷(已下线)2013-2014学年福建晋江季延中学高二上学期期中考试理数学试卷(已下线)2013-2014学年人教A版高中数学选修4-5课时提升2-1练习卷(已下线)2014届安徽省“江淮十校协作体”四月联考卷理科数学试卷(已下线)2015届福建省八县(市)一中高三上学期半期联考文科数学试卷2015届北京市月坛中学高三上学期期中考试理科数学试卷2015届辽宁省朝阳市三校协作体高三下学期开学联考理科数学试卷2016届吉林省实验中学高三上学期第一次模拟理科数学试卷12016届吉林省实验中学高三上学期第一次模拟理科数学试卷22016届浙江省瑞安市高三上学期第一次四校联考理科数学试卷2015-2016学年黑龙江省双鸭山一中高二上期末文科数学卷2015-2016学年吉林省吉林市五十五中高二上学期期末理科数学试卷2016届广东省深圳市南山区高三上学期期末文科数学试卷2015-2016学年江西省宜春市樟树中学联考高二上学期期末理科数学卷2015-2016学年江西省赣州市高二上学期期末文科数学试卷2016届浙江省宁波市“十校”高三联考理科数学试卷2015-2016学年江西省樟树中学、高安二中高二上学期期末理科数学卷2016届河南省洛阳市高三考前练习二理科数学试卷2016-2017学年河北省枣强中学高二上学期期末考试理数试卷山东省临沂市临沭县第一中学2016-2017学年高二下学期期中考试数学(理)试题2017届上海市徐汇区高三下学期二模数学试卷浙江省杭州市2016-2017学年高二下学期期末教学质量检测数学试题安徽省明光市一中2017-2018学年高二期末考试卷理科数学试题福建省莆田市第二十五中学2017-2018学年高二上学期期末考试数学(理)试题上海市嘉定区2017-2018学年高一第一学期期末考试数学试题辽宁省大连市2017-2018学年高二上学期期末考试数学(文)试题2019届高考数学人教A版理科第一轮复习单元测试题:第七章 不等式、推理与证明【全国市级联考】湖北省宜昌市协作体2017-2018学年高二下学期期末考试数学(文)试题2018年全国普通高等学校招生统一考试数学(上海卷)【市级联考】】重庆市(区县)2019年普通高等学校招生全国统一考试11月调研测试卷数学(理)试题【市级联考】重庆市(区县)2019届高三11月调研测试卷数学(文)试题浙江省宁波市鄞州中学2018-2019学年高二(上)期中考试数学试题上海市浦东新区2019届高三上学期期中考试数学试题【全国百强校】江西省南昌市第十中学2018-2019学年高二上学期第二次月考数学(文)试题【全国百强校】四川省成都市外国语学校2018-2019学年高二12月月考数学(理)试题【全国百强校】四川省成都外国语学校2018-2019学年高二12月月考数学(文)试题吉林省白城市第一中学2018-2019学年高二12月月考数学(理)试题【校级联考】吉林省白城市第一中学2018-2019学年高二上学期期末考试数学(理)试题【区级联考】北京市朝阳区2019届高三期末文科数学试题【市级联考】河南省南阳市2018-2019学年高二上学期期末考试数学(文)试题【全国百强校】上海市建平中学2018-2019学年高一上学期期中考试数学试题黑龙江省大庆市第四中学2018-2019学年高二下学期第二次月考数学(理)试题新疆伊西哈拉镇中学2018-2019学年高二上学期期末数学试卷黑龙江省牡丹江市第三高级中学2018-2019学年高二下学期期末考试数学(理)试题福建省泉州市永春县永春二中2019-2020学年高一上学期数学10月月考试题上海市曹杨二中2018-2019学年高三上学期第一次月考数学试题上海市南洋模范中学2019-2020学年高三上学期期中数学试题2019年上海市高考压轴卷数学试题山东省泰安市宁阳一中2019-2020学年高一上学期模块考试数学试题河北省石家庄市第二中学2019-2020学年高二上学期期中数学试题山东省济宁市实验中学2019-2020学年高一上学期期中数学试题上海市延安中学2018-2019学年高三上学期9月月考数学试题清华大学附属中学2019-2020学年高一上学期期中数学试题甘肃省天水市甘谷第一中学2019-2020学年高二上学期第二次月考数学(理)试题江西省宜春市靖安县靖安中学2019-2020学年高二上学期第二次月考数学(理)试题山东省淄博市淄川区般阳中学2019-2020学年高一上学期期中数学试题福建省泉州市泉港区第一中学2019-2020学年高一上学期期中数学试题海南省文昌中学2019-2020学年高二上学期第二次月考数学试题吉林省长春市榆树市2019-2020学年高二上学期期末数学(理)试题上海市黄浦区2016-2017学年高三上学期期终调研测试数学试题2017年上海市黄浦区高考一模数学试题广西壮族自治区南宁市兴宁区第三中学2019-2020学年高三上学期9月月考数学(文)试题广西壮族自治区南宁市兴宁区第三中学2019年高三上学期9月月考数学(理)试题甘肃省平凉市静宁县第一中学2019-2020学年高二上学期期末数学(理)试题人教A版(2019) 必修第一册 过关斩将 第一章 1.4. 充分条件与必要条件 1.4.1 充分条件与必要条件 1.4.2 充要条件2017届上海市杨浦区高三5月模拟考试数学试题重庆市黔江新华中学校2019-2020学年高二上学期10月月考数学试题辽宁省实验中学2019-2020学年高一上学期12月月考数学试题河北省衡水市枣强县枣强中学2019-2020学年高二上学期期末数学试题2020届天津市南开中学高三数学统练(3)2020届湖南省长沙市长郡中学高三上学期第5次月考数学(文)试题浙江省宁波市镇海区镇海中学2019-2020学年高二上学期期中数学试题宁夏六盘山高级中学2018-2019学年高二上学期第二次月考数学(文)试题2020届湖南省长沙市长郡中学高三第五次月考数学(文)试题湖南省株洲市醴陵四中2018-2019学年高二下学期期末数学(理)试题山西省晋中市平遥县第二中学2019-2020学年高二上学期12月月考数学试题广东省深圳市平冈中学2018-2019学年高二下学期第一次月考数学(文)试题辽宁省鞍山市第一中学2018-2019学年高二下学期期中数学(文)试题吉林省辽源市田家炳高级中学2018-2019学年高二下学期期末数学(文)试题全册综合测试模拟一-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第一册)-《高中新教材知识讲学》山东省泰安市肥城市2018-2019学年高二上学期期中数学试题甘肃省天水市第一中学2019-2020学年高二下学期第一次学段考试数学(文)试题2020届北京市丰台区高三一模数学试题内蒙古集宁一中2019-2020学年高二下学期第三次月考数学(理)试题浙江省浙南名校联盟2019-2020学年高二下学期期末联考数学试题陕西省西安中学2020届高三高考数学(理科)适应性试卷(三)新疆实验中学2019-2020学年高二下学期期末考试数学试题(已下线)第4节充分条件与必要条件-2020-2021学年高一数学课时同步练(新人教A版必修第一册)(已下线)【新教材精创】2.2.1不等式及其性质练习(2)-人教B版高中数学必修第—册(已下线)集合与常用逻辑用语(综合测试卷)-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)(已下线)1.4.1充分条件与必要条件-【新教材】人教A版(2019)高中数学必修第一册同步练习(已下线)【新东方】浙江省新东方2020-2021学年高一上学期课堂练习(B1)(已下线)1.4充分条件与必要条件-2020-2021学年高一数学同步课堂帮帮帮(人教A版2019必修第一册)(已下线)第2章一元二次函数、方程和不等式章末检测-【新教材】人教A版(2019)高中数学必修第一册限时作业陕西省商洛市商丹高新学校2019-2020学年高二下学期期中数学(理)试题(已下线)专题02 常用逻辑用语-十年(2011-2020)高考真题数学分项(已下线)专题09 常用逻辑用语-2020年高考数学母题题源解密(北京专版)(已下线)【新东方】浙江省2020-2021学年高一上学期第一次月考数学试题【JTX】安徽省阜阳市太和中学2019-2020学年高二下学期开学考试数学(文)试题江苏省南通市启东中学2020-2021学年高三上学期期初数学试题广西南宁三中2020届高三数学理科考试二试题广东省中山市纪念中学2020-2021学年高一上学期10月月考数学试题上海市南洋模范中学2021届高三上学期9月月考数学试题广东省广东实验中学2020-2021学年高一上学期第一次段考数学试题广西贵港高中2020-2021学年高二上学期理科期中教学质量监测试题安徽省安庆市怀宁县第二中学2020-2021学年高一上学期期中数学试题宁夏青铜峡市高级中学2021届高三上学期期中考试数学(理)试题山东省济南市第一中学2020-2021学年高一上学期期中考试数学试题北京市第一六一中学2021届高三上学期期中考试数学试题福建省福州第三中学2020-2021学年高一上学期半期考数学试题江苏省徐州市2020-2021学年高二上学期期中数学试题福建省厦门市第一中学2020-2021学年度高一数学12月适应性练习试题山东省济宁市任城区2020-2021学年高一上学期期中考试数学试题福建省南安市国光中学2020-2021学年高一上学期期中考试数学试题 广东省深圳市宝安第一外国语学校2020-2021学年高一上学期期中数学试题河北省石家庄二中2020-2021学年高一(上)期中数学试题(已下线)热点01 集合与逻辑-2021年高考数学【热点·重点·难点】专练(上海专用)河北省晋州市第二中学2020-2021学年高二上学期期中数学试题天津市静海区瀛海学校2020-2021学年高三上学期10月检测数学试题湖南省常德市临澧县第一中学2020-2021学年高一上学期期中数学试题江苏省淮安市2020-2021学年高二上学期期末数学试题北京市大兴区2020~2021学年高一上学期期末检测数学试题北京市石景山区2020-2021学年高一上学期期末数学试题湖南省张家界市2020-2021学年高二上学期期末数学试题湖南省岳阳市平江县第一中学2020-2021学年高二上学期1月阶段性检测数学试题北京市第四十三中学2020-2021学年高一12月月考数学试题安徽省六安市新安中学2020-2021学年高二下学期入学考试数学(文)试题安徽省六安市新安中学2020-2021学年高二下学期入学考试数学(理)试题(已下线)【新东方】杭州新东方高中数学试卷335(已下线)考点03 充分条件与必要条件-备战2021年高考数学经典小题考前必刷(新高考地区专用)广东省深圳市菁华学校2020-2021学年高二上学期12月月考数学试题新疆乌苏市第一中学2020-2021学年高二(网班)下学期入学检测数学试题广东省东莞市光明中学2020-2021学年高一上学期期中数学试题上海市格致中学2021届高三三模数学试题辽宁省名校联盟2020-2021学年高二6月份联合考试数学试题 辽宁省重点中学2020-2021学年高二6月联考数学试题江苏省泰州市靖江市斜桥中学与刘国钧中学2020-2021学年高一上学期联考数学试题(已下线)第02章 常用逻辑用语(B卷提升卷)-2020-2021学年高一数学必修第一册同步单元AB卷(新教材苏教版)四川省南充高级中学2020-2021学年高二下学期入学考试数学(文)试题四川省南充高级中学2020-2021学年高二下学期入学考试数学(理)试题(已下线)解密02 常用逻辑用语(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)考点突破02 一元二次函数-备战2022年高考数学一轮复习培优提升精炼(新高考地区专用)山东省济宁市2020-2021学年高二下学期期末数学试题福建省福州市罗源县第二中学2020-2021学年高一12月月考数学试题广西蒙山县蒙山中学2020-2021学年高二下学期第一次月考数学(文)试题(已下线)第2章 常用逻辑用语(B卷-提升卷)-2021-2022学年高一数学同步单元AB卷(苏教版2019必修第一册)【学科网名师堂】(已下线)专练05 充分条件与必要条件-2021-2022学年高一数学上册同步课后专练(人版A版必修第一册)(已下线)江苏省南通市如皋市2021-2022学年高一上学期期初调研数学试题湖南省长沙市长郡中学2021-2022学年高二上学期入学考试数学试题上海奉贤区曙光中学2020-2021学年高一上学期10月月考数学试题江西省靖安中学2019-2020学年高二上学期第二次月考数学(理)试题内蒙古自治区赤峰市赤峰二中2019-2020学年高二上学期11月月考数学(理)试题(已下线)专题03 常用逻辑用语-五年(2017-2021)高考数学真题分项(新高考地区专用)安徽省蚌埠市五河第一中学2021-2022学年高二上学期第一次月考数学试题福建省莆田市莆田第二中学2022届高三10月月考数学试题安徽省阜阳市第一中学2021-2022学年高一上学期第一次月考数学试题黑龙江省牡丹江市第一高级中学2021-2022学年高一上学期10月月考数学试题北京市海淀实验中学2020-2021学年高一10月份月考数学试题福建省宁德市重点高中2022届高三10月月考数学试题浙江省绍兴市越清崧联盟2021-2022学年高一上学期期中联考数学试题 天津市南开区南大奥宇培训学校2021-2022学年高二上学期摸底考试数学试题江苏省常州市田家炳高级中学2021-2022学年高一10月份调研数学试题广东省深圳市高级中学等九校2022届高三上学期11月联考数学试题浙江省舟山中学2021-2022学年高一上学期期中数学试题重庆市铁路中学2021-2022学年高一上学期期中数学试题上海市普陀区2022届高三上学期11月调研测试(0.5模)数学试题黑龙江省牡丹江市第三中学2021-2022学年高三上学期第一次月考数学(文)试题浙江省9+1高中联盟2021-2022学年高一上学期期中联考数学试题黑龙江省牡丹江市第三中学2021-2022学年高三上学期第二次月考数学(文)试题苏教版(2019) 必修第一册 过关检测 第2章 高考专练 常用逻辑用语天津市滨海新区塘沽第一中学2021-2022学年高一上学期期中数学试题北京市第一六一中学2021-2022学年高一上学期期中阶段测试数学试题河北省石家庄四中2021-2022学年高一上学期期中数学试题沪教版(2020) 必修第一册 堂堂清 第二章 2.1(3)等式与不等式的性质北京市第四十三中学2022届高三上学期期中考试数学试题海南省海口市海港学校2022届高三上学期第四次考试数学试题(已下线)专题9.1 期中押题检测卷(考试范围:第1-4章) 1(易)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(苏教版2019必修第一册)吉林省长春市东北师范大学附属中学2021-2022学年高一上学期期中数学试题(已下线)第02讲 一元二次函数、方程和不等式-【寒假自学课】2022年高一数学寒假精品课(人教A版2019必修第一册)广西蒙山县第一中学2021-2022学年高二上学期第二次月考数学(理)试题天津市第二南开学校2021-2022学年高一上学期期中数学试题广东省梅州市丰顺县、五华县2022届高三上学期一模数学试题山西省朔州市朔城区第一中学校2021-2022学年高一下学期开学检测数学试题广东省化州市第三中学2020-2021学年高一下学期期中数学试题(已下线)第二章 一元二次函数、方程和不等式 综合检测-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)辽宁省名校联盟2021-2022学年高一3月联合考试数学试题(已下线)专题02 逻辑用语与命题100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)新疆石河子第二中学2021-2022学年高一上学期第二次月考数学试题新疆生产建设兵团第十师北屯高级中学2021-2022学年高一10月月考数学试题河北省武强中学2021-2022学年高一上学期期中数学试题四川省泸州市泸县第四中学2021-2022学年高二下学期第一学月(3月)考试文科数学试题四川省泸州市泸县第四中学2021-2022学年高二下学期第一学月(3月)考试理科数学试题重庆市南开中学校2021-2022学年高一下学期第一次月考数学试题天津市新华中学2022届高三下学期4月统练数学试题江西省赣州市第三中学2021-2022学年高一下学期期中考试数学试题(已下线)必刷卷02(文)-2022年高考数学考前信息必刷卷(全国乙卷)(已下线)必刷卷02(理)-2022年高考数学考前信息必刷卷(全国乙卷)湖北省重点高中智学联盟2021-2022学年高二下学期5月联考数学试题广东省深圳科学高中2021-2022学年高一下学期期中数学试题四川省凉山州宁南中学2021-2022学年高二下学期第二次月考数学(文)试题江西省吉安市第一中学2021-2022学年高二下学期第一次段考数学(文)试题江西省吉安市第一中学2021-2022学年高二下学期第一次段考数学(理)试题北京市第八中学2021-2022学年高二6月月考数学试题河北省大名县第一中学2021-2022学年高一上学期第一次月考数学试题浙江省丽水市2021-2022学年高二下学期普通高中教学质量监控(期末)数学试题(已下线)1.2 逻辑用语与充分、必要条件(精练)-【一隅三反】2023年高考数学一轮复习(基础版)(新高考地区专用)北京市北京理工大学附属中学2021-2022学年高二下学期限时训练15(期末模拟)试题陕西省咸阳市武功县普集高中2021-2022学年高二下学期第三次月考文科数学试题宁夏青铜峡市宁朔中学2021-2022学年高二下学期期末考试数学(文)试题宁夏银川市第二中学2021-2022学年高二下学期期末考试数学(文)试题(已下线)第01讲 集合与常用逻辑用语(练)-2023年高考数学一轮复习讲练测(全国通用)天津市滨海新区塘沽第一中学2022届高三下学期4月统练数学试题(已下线)专题62:基本不等式-2023届高考数学一轮复习精讲精练(新高考专用)新疆霍城县第二中学2021-2022学年高二下学期期末考试数学(文)试题(已下线)2.2 充分条件、必要条件、充要条件(1)北京市景山学校2023届高三上学期开学摸底测试数学试题第二章 一元二次函数、方程和不等式(B卷·能力提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)北京师范大学附属中学2023届高三上学期数学第二次大单元练习题数学试题福建省厦门外国语学校2023届高三上学期10月月考数学试题湖北省恩施咸丰春晖学校2022-2023学年高一上学期9月月考数学试题广东省广州市执信中学2023届高三上学期十月月考数学试题广东省广州英豪学校2022-2023学年高一上学期第一次月考数学试题吉林省吉林市第四中学2022-2023学年高一上学期第一次月考数学试题河北省文安县第一中学2022-2023学年高一上学期10月月考数学试题安徽省芜湖顶峰艺术学校2022-2023学年高一上学期9月质量检测数学试题山西省晋城市第一中学校2022-2023学年高一上学期11月月考(第四次调研)数学试题广东省深圳市盐田高级中学2021-2022学年高一上学期期中数学试题广东省揭阳市揭东区第二中学2023届高三上学期第一次月考数学试题天津市五校(杨村、宝坻、蓟州、芦台、静海一中)2022-2023学年高一上学期期中联考数学试题陕西省咸阳市武功县普集高级中学2020-2021学年高三上学期第一次月考理科数学试题北京市第十五中学南口学校2022-2023学年高一上学期期中考试数学试题宁夏青铜峡市宁朔中学2023届高三上学期期中考试数学(理)试题河南省郑州市郑州优胜实验中学2022-2023学年高一上学期10月月考数学试题辽宁省辽西联合校2022-2023学年高三上学期期中考试数学试题宁夏银川市贺兰县景博中学2023届高三上学期期中考试数学(文)试题甘肃省白银市会宁县会宁县第四中学2022-2023学年高一上学期期中数学试题吉林省长春市农安县2022-2023学年高一上学期期中数学试题陕西省咸阳市兴平市南郊高级中学2022-2023学年高一上学期第一次质量检测数学试题黑龙江省哈尔滨市第一中学校2022-2023学年高一上学期期中数学试题2023年1月广东省普通高中学业水平合格性考试模拟三数学试题辽宁省沈阳市东北育才学校高中部2020-2021学年高一上学期第一次段考数学试题天津市实验中学滨海学校2022-2023学年高三上学期期末数学试题广东省江门市培英高级中学2022-2023学年高一上学期期中数学试题四川省泸州市古蔺县金兰高级中学校2022-2023学年高三上学期第一次月考数学(文)试题山东省济宁市邹城市第一中学2022-2023学年高三下学期月考一数学试题1.2常用逻辑用语-2022-2023学年高一上学期数学北师大版2019必修第一册1.2.1 必要条件与充分条件-2021-2022学年高一上学期数学北师大版2019必修第一册2.1 充分条件与必要条件-2021-2022学年高一数学北师大版2019必修第一册湖南省益阳市桃江县2022-2023学年高二下学期期末数学试题广东省深圳市宝安区深圳市新安中学(集团)高中部2022-2023学年高一上学期期中数学试题黑龙江省双鸭山市红兴隆第一高级中学2022-2023学年高一下学期期中数学试题云南省建水县第二中学2022-2023学年高二下学期期中检测数学试题甘肃省临夏州临夏中学2021-2022学年高二下学期期中考试(文科)数学试题河北省唐县第一中学2022-2023学年高一上学期10月月考数学试题黑龙江省齐齐哈尔市第八中学校2022-2023学年高一上学期期中数学试题2024年广东省普通高中学业水平合格性考试模拟(二)数学试题四川省巴中市恩阳区2022-2023学年高一上学期期中数学试题江苏省南京市燕子矶中学2023-2024学年高一上学期9月学分认定考试数学试题福建省永春第二中学2023-2024学年高一上学期10月月考数学试题江苏省宿迁市泗阳县实验高级中学2023-2024学年高一上学期第一次调研测试数学试题陕西师范大学附属中学2023-2024学年高一上学期10月月考数学试题湖南省株洲市南方中学2023-2024学年高一上学期期中数学试题河南省信阳市新县高级中学2024届高三适应性考试(七)数学试题福建省三明第一中学2024-2025学年高一上学期10月月考数学试题上海市嘉定区第一中学2024-2025学年高三上学期10月阶段性检测数学试卷湖南省长沙市长郡中学2024-2025学年高一上学期10月月考数学试题河南省驻马店市新蔡县第一高级中学2024-2025学年高一上学期10月月考数学试题吉林省通化市梅河口市第五中学2024-2025学年高一上学期10月期中考试数学试题
名校
2 . 已知空间中两个不重合的平面 和平面
和平面 ,直线
,直线 平面
平面 ,则“
,则“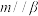 ”是“
”是“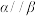 ”的( )
”的( )
 和平面
和平面 ,直线
,直线 平面
平面 ,则“
,则“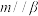 ”是“
”是“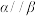 ”的( )
”的( )| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2024-09-07更新
|
311次组卷
|
3卷引用:贵州省遵义市第四中学2024-2025学年高二上学期入学质量监测数学试题
3 . 如图,四棱锥 中,底面
中,底面 为等腰梯形,平面
为等腰梯形,平面 平面
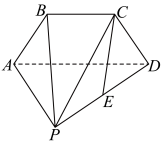
平面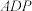 ,
,
 .
. 为
为 上一点,
上一点,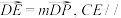 平面
平面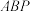 ,求
,求 的值:
的值:
(2)平面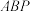 与平面
与平面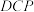 的交线为
的交线为 ,求
,求 与平面
与平面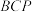 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为等腰梯形,平面
为等腰梯形,平面 平面
平面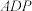 ,
,
 .
.
 为
为 上一点,
上一点,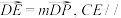 平面
平面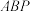 ,求
,求 的值:
的值:(2)平面
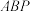 与平面
与平面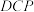 的交线为
的交线为 ,求
,求 与平面
与平面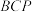 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-08-18更新
|
237次组卷
|
2卷引用:贵州省贵阳市2024-2025学年高三上学期八月摸底考试数学试题
名校
4 . 已知 ,椭圆
,椭圆 :
: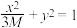 ,
, :
: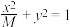 的离心率分别为
的离心率分别为 ,
, .若
.若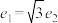 ,则
,则 的值可能为( )
的值可能为( )
 ,椭圆
,椭圆 :
: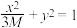 ,
, :
: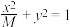 的离心率分别为
的离心率分别为 ,
, .若
.若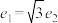 ,则
,则 的值可能为( )
的值可能为( )A.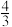 | B.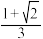 | C.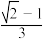 | D. |
您最近一年使用:0次
5 . 已知点 ,点
,点 在以
在以 为直径的圆上运动,
为直径的圆上运动,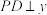 轴,垂足为
轴,垂足为 ,点
,点 满足
满足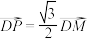 ,点
,点 的轨迹为
的轨迹为 .
.
(1)求 的方程:
的方程:
(2)过点 的直线
的直线 交
交 于点
于点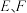 ,设直线
,设直线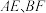 的斜率分别为
的斜率分别为 、
、 ,证明
,证明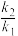 为定值,并求出该定值.
为定值,并求出该定值.
 ,点
,点 在以
在以 为直径的圆上运动,
为直径的圆上运动,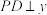 轴,垂足为
轴,垂足为 ,点
,点 满足
满足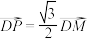 ,点
,点 的轨迹为
的轨迹为 .
.(1)求
 的方程:
的方程:(2)过点
 的直线
的直线 交
交 于点
于点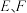 ,设直线
,设直线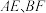 的斜率分别为
的斜率分别为 、
、 ,证明
,证明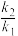 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
2024-08-17更新
|
632次组卷
|
3卷引用:贵州省贵阳市2024-2025学年高三上学期八月摸底考试数学试题
解题方法
6 . 已知双曲线 的右焦点为
的右焦点为 ,过
,过 的直线
的直线 与
与 交于点
交于点 ,且满足
,且满足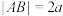 的直线
的直线 恰有三条,则双曲线
恰有三条,则双曲线 的离心率的取值范围为
的离心率的取值范围为______ .
 的右焦点为
的右焦点为 ,过
,过 的直线
的直线 与
与 交于点
交于点 ,且满足
,且满足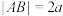 的直线
的直线 恰有三条,则双曲线
恰有三条,则双曲线 的离心率的取值范围为
的离心率的取值范围为
您最近一年使用:0次
2024-08-17更新
|
375次组卷
|
3卷引用:贵州省贵阳市2024-2025学年高三上学期八月摸底考试数学试题
名校
解题方法
7 . 如图,在长方体 中,
中, ,点
,点 为线段
为线段 上动点(包括端点),则下列结论正确的是( )
上动点(包括端点),则下列结论正确的是( )
 中,
中, ,点
,点 为线段
为线段 上动点(包括端点),则下列结论正确的是( )
上动点(包括端点),则下列结论正确的是( )
A.当点 为 为 中点时, 中点时,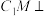 平面 平面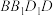 |
B.当点 为 为 中点时,直线 中点时,直线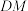 与直线 与直线 所成角的余弦值为 所成角的余弦值为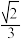 |
C.当点 在线段 在线段 上运动时,三棱锥 上运动时,三棱锥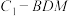 的体积是定值 的体积是定值 |
D.点 到直线 到直线 距离的最小值为 距离的最小值为 |
您最近一年使用:0次
2024-08-17更新
|
1910次组卷
|
5卷引用:贵州省贵阳市2024-2025学年高三上学期八月摸底考试数学试题
名校
解题方法
8 . 已知双曲线 :
: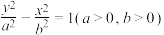 的一个焦点与抛物线
的一个焦点与抛物线 :
: 的焦点
的焦点 重合,且
重合,且 被
被 的准线
的准线 截得的弦长为
截得的弦长为 .
.
(1)求 的方程;
的方程;
(2)若过 的直线与
的直线与 的上支交于
的上支交于 ,
, 两点,设
两点,设 为坐标原点,求
为坐标原点,求 的取值范围.
的取值范围.
 :
: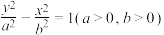 的一个焦点与抛物线
的一个焦点与抛物线 :
: 的焦点
的焦点 重合,且
重合,且 被
被 的准线
的准线 截得的弦长为
截得的弦长为 .
.(1)求
 的方程;
的方程;(2)若过
 的直线与
的直线与 的上支交于
的上支交于 ,
, 两点,设
两点,设 为坐标原点,求
为坐标原点,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 如图,平行六面体 的所有棱长均为2,
的所有棱长均为2, ,
, ,
, 两两所成夹角均为
两两所成夹角均为 ,点
,点 ,
, 分别在棱
分别在棱 ,
, 上,且
上,且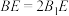 ,
,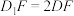 ,则( )
,则( )
 的所有棱长均为2,
的所有棱长均为2, ,
, ,
, 两两所成夹角均为
两两所成夹角均为 ,点
,点 ,
, 分别在棱
分别在棱 ,
, 上,且
上,且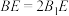 ,
,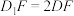 ,则( )
,则( )
A. , , , , , , 四点共面 四点共面 |
B.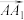 在 在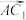 方向上的投影向量为 方向上的投影向量为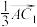 |
C.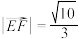 |
D.直线 与 与 所成角的余弦值为 所成角的余弦值为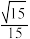 |
您最近一年使用:0次
2024-08-17更新
|
935次组卷
|
4卷引用:贵州省黔东南苗族侗族自治州2024-2025学年高三上学期开学联考数学试题
解题方法
10 . 在三棱锥 中,
中, ,
,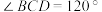 ,
, ,
, 为线段
为线段 的中点.
的中点.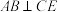 .
.
(2)求平面 与平面
与平面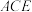 夹角的余弦值.
夹角的余弦值.
 中,
中, ,
,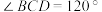 ,
, ,
, 为线段
为线段 的中点.
的中点.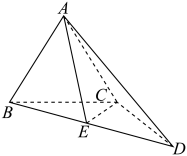
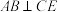 .
.(2)求平面
 与平面
与平面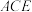 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次



