名校
解题方法
1 . 已知椭圆 过点
过点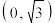 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线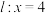 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求证:直线 与
与 的斜率之积为定值;
的斜率之积为定值;
(3)判断三点 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
 过点
过点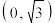 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线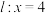 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求证:直线
 与
与 的斜率之积为定值;
的斜率之积为定值;(3)判断三点
 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
1856次组卷
|
11卷引用:【区级联考】北京市昌平区2019届高三第一学期期末数学(文)试题
【区级联考】北京市昌平区2019届高三第一学期期末数学(文)试题(已下线)2020届北京四中高三第二学期开学考试数学试题江苏省金陵中学集团南京市人民中学2021-2022学年高二上学期10月月考数学试题上海市2022届高三上学期一模暨春考模拟卷(五)数学试题北京市第八中学2023届高三上学期10月月考数学试题上海市青浦高级中学2022届高三下学期3月月考数学试题北京市西城区回民学校2024届高三上学期12月月考数学试题天津市滨海新区塘沽紫云中学2024届高三上学期期末模拟数学试题(六)福建省莆田市第二中学2023-2024学年高二下学期返校考试数学试卷(已下线)第10题 椭圆中的一类定值问题 (压轴题)广东省深圳市翠园中学2024-2025学年高二上学期期中考试数学试题
13-14高三·全国·课后作业
名校
解题方法
2 . 如图所示,四边形ABCD是边长为3的正方形, 平面ABCD,
平面ABCD, ,
, ,BE与平面ABCD所成角为60°.
,BE与平面ABCD所成角为60°.
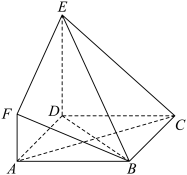
(1)求证: 平面BDE;
平面BDE;
(2)求二面角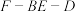 的余弦值;
的余弦值;
(3)设点M是线段BD上的一个动点,试确定点M的位置,使得 平面BEF,并证明你的结论.
平面BEF,并证明你的结论.
 平面ABCD,
平面ABCD, ,
, ,BE与平面ABCD所成角为60°.
,BE与平面ABCD所成角为60°.
(1)求证:
 平面BDE;
平面BDE;(2)求二面角
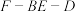 的余弦值;
的余弦值;(3)设点M是线段BD上的一个动点,试确定点M的位置,使得
 平面BEF,并证明你的结论.
平面BEF,并证明你的结论.
您最近一年使用:0次
2021-11-11更新
|
1883次组卷
|
27卷引用:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法
(已下线)2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法北京东城171中2016-2017学年高二上期中数学(理)试题北京市朝阳区第80中学2017届高三上12月月考数学试题辽宁省丹东市2017-2018学年高二数学理科上学期期末考试试题河北省衡水市阜城中学2017-2018学年高二上学期第五次月考数学(理)试题北京市朝阳区80中学2017届高三上学期12月月考数学(理)试题【全国百强校】2018年天津市南开中学高三模拟考试数学(理)2018-2019人教A版高中数学选修2-1第三章 空间向量与立体几何 章末评估验收(三)【全国百强校】天津市南开中学2018-2019学年高三(下)第四次月考数学试题(理科)(2月份)(已下线)第01章+章末复习课(重点练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第一册)山东省滕州市第一中学2020-2021学年高二9月开学收心考试数学试题人教B版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 本章复习提升(已下线)3.5 章末复习课(重点练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-1)重庆十八中两江实验中学2020-2021学年高二上学期12月月考数学试题福建省南平市浦城县2021届高三上学期期中测试数学试题北京市海淀区北京理工大学附属中学2020-2021学年高二上学期期中考试数学试题北京市西城区北京师范大学第二附属中学2022届高三上学期期中数学试题江苏省苏州第十中学2022届高三下学期3月阶段检测数学试题云南省大理下关第一中学教育集团2021-2022学年高二上学期段考数学试卷(一)试题(已下线)考点52 空间向量在立体几何中的运用-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】河北省邢台市第一中学2021-2022学年高二上学期第三次月考数学试题(已下线)考点31 直线、平面平行与垂直的判定与性质-备战2022年高考数学典型试题解读与变式(已下线)重难点03 空间向量与立体几何-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)一轮巩固卷02-【赢在高考·黄金20卷】备战2022年高考数学模拟卷(新高考专用)(已下线)2022年高考考前20天终极冲刺攻略(三)【理科数学】 (5月27日)宁夏育才中学2022-2023学年高二下学期开学考试理科数学试题北京市第一七一中学2023-2024学年高二上学期期中调研数学试题
3 . 设直线 ,曲线
,曲线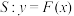 .若直线
.若直线 与曲线
与曲线 同时满足下列两个条件:①直线
同时满足下列两个条件:①直线 与曲线
与曲线 相切且至少有两个切点;②对任意
相切且至少有两个切点;②对任意 都有
都有 .则称直线
.则称直线 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(1)已知函数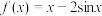 .求证:
.求证: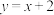 为曲线
为曲线 的“上夹线”;
的“上夹线”;
(2)观察下图: 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
 ,曲线
,曲线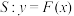 .若直线
.若直线 与曲线
与曲线 同时满足下列两个条件:①直线
同时满足下列两个条件:①直线 与曲线
与曲线 相切且至少有两个切点;②对任意
相切且至少有两个切点;②对任意 都有
都有 .则称直线
.则称直线 为曲线
为曲线 的“上夹线”.
的“上夹线”.(1)已知函数
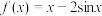 .求证:
.求证: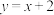 为曲线
为曲线 的“上夹线”;
的“上夹线”;(2)观察下图:

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
您最近一年使用:0次
4 . 知椭圆 的左、右顶点分别为
的左、右顶点分别为  ,点
,点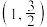 该椭圆上,且该椭圆的右焦点
该椭圆上,且该椭圆的右焦点 与抛物线
与抛物线  的焦点重合.
的焦点重合.
(1)求椭圆 的标准方程;
的标准方程;
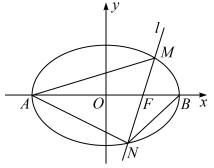
(2)如图,过点 且斜率为
且斜率为 的直线
的直线 与椭圆交于
与椭圆交于 两点,记直线
两点,记直线 的斜率为
的斜率为  ,直线
,直线 的斜率为
的斜率为 ,直线
,直线 的斜率
的斜率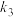 ,求证:_____________.
,求证:_____________.
在以下三个结论中选择一个填在横线处进行证明.
①直线 与
与 的交点在定直线
的交点在定直线 上;
上;
② ;
;
③ .
.
 的左、右顶点分别为
的左、右顶点分别为  ,点
,点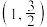 该椭圆上,且该椭圆的右焦点
该椭圆上,且该椭圆的右焦点 与抛物线
与抛物线  的焦点重合.
的焦点重合.(1)求椭圆
 的标准方程;
的标准方程;(2)如图,过点
 且斜率为
且斜率为 的直线
的直线 与椭圆交于
与椭圆交于 两点,记直线
两点,记直线 的斜率为
的斜率为  ,直线
,直线 的斜率为
的斜率为 ,直线
,直线 的斜率
的斜率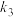 ,求证:_____________.
,求证:_____________.
在以下三个结论中选择一个填在横线处进行证明.
①直线
 与
与 的交点在定直线
的交点在定直线 上;
上;②
 ;
;③
 .
.
您最近一年使用:0次
20-21高二上·全国·单元测试
解题方法
5 . 设集合W由满足下列两个条件的数列{an}构成:①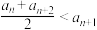 ;②存在实数M,使an≤M(n为正整数)
;②存在实数M,使an≤M(n为正整数)
(1)在只有5项的有限数列{an}、{bn}中,其中a1=1,a2=2,a3=3,a4=4,a5=5,b1=1,b2=4,b3=5,b4=4,b5=1,试判断数列{an}、{bn}是否为集合W中的元素;
(2)设{cn}是等差数列,sn是其前n项和,c3=4,s3=18,证明数列{sn}∈W,并写出M的取值范围;
(3)设数列{dn}∈W,对于满足条件的M的最小值M0,都有dn≠M0(n∈N*)求证:数列{dn}单调递增.
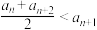 ;②存在实数M,使an≤M(n为正整数)
;②存在实数M,使an≤M(n为正整数)(1)在只有5项的有限数列{an}、{bn}中,其中a1=1,a2=2,a3=3,a4=4,a5=5,b1=1,b2=4,b3=5,b4=4,b5=1,试判断数列{an}、{bn}是否为集合W中的元素;
(2)设{cn}是等差数列,sn是其前n项和,c3=4,s3=18,证明数列{sn}∈W,并写出M的取值范围;
(3)设数列{dn}∈W,对于满足条件的M的最小值M0,都有dn≠M0(n∈N*)求证:数列{dn}单调递增.
您最近一年使用:0次
6 . 如图,在三棱柱 中,
中, ,D,E分别是
,D,E分别是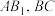 的中点.求证:
的中点.求证: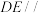 平面
平面 ;
;
(2) 平面
平面 .(用向量方法证明)
.(用向量方法证明)
 中,
中, ,D,E分别是
,D,E分别是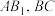 的中点.求证:
的中点.求证:
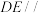 平面
平面 ;
;(2)
 平面
平面 .(用向量方法证明)
.(用向量方法证明)
您最近一年使用:0次
2020-08-12更新
|
584次组卷
|
6卷引用:【市级联考】江苏省南京市、盐城市2019届高三第二次模拟考试数学试题
【市级联考】江苏省南京市、盐城市2019届高三第二次模拟考试数学试题人教A版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 专题强化练1 利用空间向量基本定理解决立体几何问题(已下线)考点40 立体几何中的向量方法-证明平行与垂直关系(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)1.1 空间向量及其运算-2021-2022学年高二数学尖子生同步培优题典(人教A版2019选择性必修第一册)(已下线)第02讲 空间向量基本定理(教师版)-【帮课堂】【典例题】 3.2.1 向量共面的充要条件 课堂例题-沪教版(2020)选择性必修第一册第3章 空间向量及其应用
解题方法
7 . 已知 :
: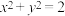 交
交 轴于
轴于 ,
, 两点,过以
两点,过以 为长轴,离心率为
为长轴,离心率为 的椭圆
的椭圆 的左焦点
的左焦点 的直线
的直线 交椭圆
交椭圆 于
于 ,
, ,分别交
,分别交 轴和圆
轴和圆 于
于 ,
, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若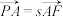 ,
, .求证:
.求证: 为定值;
为定值;
(3)过原点 作直线
作直线 的垂线交直线
的垂线交直线 于点
于点 .试探究:当点
.试探究:当点 在圆
在圆 上运动时(不与
上运动时(不与 ,
, 重合),直线
重合),直线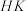 与圆
与圆 是否保持相切?若是,请证明;若不是,请说明理由.
是否保持相切?若是,请证明;若不是,请说明理由.
 :
: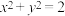 交
交 轴于
轴于 ,
, 两点,过以
两点,过以 为长轴,离心率为
为长轴,离心率为 的椭圆
的椭圆 的左焦点
的左焦点 的直线
的直线 交椭圆
交椭圆 于
于 ,
, ,分别交
,分别交 轴和圆
轴和圆 于
于 ,
, .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若
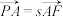 ,
, .求证:
.求证: 为定值;
为定值;(3)过原点
 作直线
作直线 的垂线交直线
的垂线交直线 于点
于点 .试探究:当点
.试探究:当点 在圆
在圆 上运动时(不与
上运动时(不与 ,
, 重合),直线
重合),直线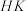 与圆
与圆 是否保持相切?若是,请证明;若不是,请说明理由.
是否保持相切?若是,请证明;若不是,请说明理由.
您最近一年使用:0次
2020-07-29更新
|
231次组卷
|
3卷引用:高二上学期期末综合测试二+(B卷提升卷)-2020-2021学年高二数学上学期同步单元AB卷(苏教版,新课改地区专用)
(已下线)高二上学期期末综合测试二+(B卷提升卷)-2020-2021学年高二数学上学期同步单元AB卷(苏教版,新课改地区专用)开卷教育联盟2020届全国高三模拟考试(四)数学理科试题湖北省武汉市蔡甸区实验高级中学2020-2021学年高二上学期10月联考数学试题
名校
解题方法
8 . 已知椭圆 ,点A、点B分别是椭圆上关于原点对称的两点,点P是椭圆上不同于点A和点B的任意一点.
,点A、点B分别是椭圆上关于原点对称的两点,点P是椭圆上不同于点A和点B的任意一点.
(1)求证:直线PA的斜率与直线PB的斜率之积为定值,并求出该定值;
(2)试对双曲线 写出具有类似特点的正确结论,并加以证明.
写出具有类似特点的正确结论,并加以证明.
 ,点A、点B分别是椭圆上关于原点对称的两点,点P是椭圆上不同于点A和点B的任意一点.
,点A、点B分别是椭圆上关于原点对称的两点,点P是椭圆上不同于点A和点B的任意一点.(1)求证:直线PA的斜率与直线PB的斜率之积为定值,并求出该定值;
(2)试对双曲线
 写出具有类似特点的正确结论,并加以证明.
写出具有类似特点的正确结论,并加以证明.
您最近一年使用:0次
9 . 如图,在三棱柱ABC−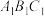 中,
中, 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为 ,AC,
,AC, ,
, 的中点,AB=BC=
的中点,AB=BC= ,AC=
,AC= =2.
=2.
(2)求二面角B−CD−C1的余弦值;
(3)证明:直线FG与平面BCD相交.
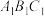 中,
中, 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为 ,AC,
,AC, ,
, 的中点,AB=BC=
的中点,AB=BC= ,AC=
,AC= =2.
=2.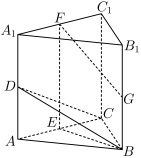
(2)求二面角B−CD−C1的余弦值;
(3)证明:直线FG与平面BCD相交.
您最近一年使用:0次
2018-06-09更新
|
15375次组卷
|
35卷引用:江苏省徐州市侯集高级中学2019-2020学年高二上学期期末数学试题
江苏省徐州市侯集高级中学2019-2020学年高二上学期期末数学试题2018年全国普通高等学校招生统一考试理科数学(北京卷)(已下线)2018年高考题及模拟题汇编 【理科】5.立体几何【全国百强校】江西省南昌市第十中学2017-2018学年高二下学期期末考试数学(理)试题北京市2019届高三数学理一轮复习典型题专项训练:立体几何【全国百强校】山西省祁县中学2018-2019学年高二上学期期末模拟一考试数学(理)试题四川省棠湖中学2018-2019学年高二上学期期末考试数学(理)试题(已下线)专题8.6 空间向量及空间位置关系(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题8.6 空间向量及空间位置关系(讲)【理】-《2020年高考一轮复习讲练测》2020届北京市昌平区新学道临川学校高三上学期第三次月考数学(理)试题2020届北京市昌平区新学道临川学校高三上学期第三次月考数学(文)试题(已下线)专题06 立体几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题17 立体几何综合-五年(2016-2020)高考数学(理)真题分项山西省山西大学附中2019-2020学年高二(12月份)第四次诊断数学(理科)试题(已下线)专题8.6 空间向量及其运算和空间位置关系(精讲)--2021年高考数学(理)一轮复习讲练测(已下线)专题8.6 空间向量及其运算和空间位置关系(精讲)-2021年高考数学(理)一轮复习学与练四川省成都市双流区棠湖中学2018-2019学年高二上学期期末数学(理)试题云南省昭通市昭阳第一中学2020-2021学年高一12月月考数学(理)试题(已下线)专题8.7 立体几何中的向量方法(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题24 空间向量与空间角的计算-十年(2011-2020)高考真题数学分项(已下线)专题4.4 空间向量与立体几何-2021年高考数学解答题挑战满分专项训练(新高考地区专用)北京市第四十三中学2020-2021学年高二下学期第一次月考数学试题(已下线)专题10 立体几何-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)第37讲 立体几何中的向量方法 (讲) — 2022年高考数学一轮复习讲练测(课标全国版)福建省泉州科技中学2021-2022学年高二上学期第一次月考数学试题北京市昌平区第一中学2021-2022学年高二上学期期中考试数学试题北京市景山学校2021-2022学年高二上学期期中考试数学试题辽宁省沈阳市五校协作体2021-2022学年高二上学期期中数学试题北京市第九中学2022届高三12月统练(月考)数学试题(已下线)重组卷03北京外国语大学附属中学2022届高三模拟数学试题北京十年真题专题07立体几何与空间向量北京市第一零一中学2023-2024学年高三上学期数学统练五云南省大理白族自治州民族中学2023-2024学年高二下学期5月期中数学试题专题09立体几何与空间向量(第二部分)
名校
解题方法
10 . 已知椭圆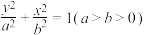 过点
过点 ,离心率为
,离心率为 .
.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线 交抛物线
交抛物线 于
于 、
、 两点,
两点, 为原点.
为原点.
①求证: ;
;
②设 、
、 分别与椭圆相交于
分别与椭圆相交于 、
、 两点,过原点
两点,过原点 作直线
作直线 的垂线
的垂线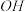 ,垂足为
,垂足为 ,证明:
,证明: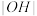 为定值.
为定值.
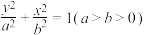 过点
过点 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线
 交抛物线
交抛物线 于
于 、
、 两点,
两点, 为原点.
为原点.①求证:
 ;
;②设
 、
、 分别与椭圆相交于
分别与椭圆相交于 、
、 两点,过原点
两点,过原点 作直线
作直线 的垂线
的垂线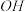 ,垂足为
,垂足为 ,证明:
,证明: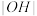 为定值.
为定值.
您最近一年使用:0次
2017-11-29更新
|
1328次组卷
|
4卷引用:江苏省淮安市六校(洪泽中学、金湖中学等)2020-2021学年高二上学期第三次联考数学试题



