名校
解题方法
1 . 某校为了庆祝建校100周年,举行校园文化知识竞赛.某班经过层层选拔,还有最后一个参赛名额要在甲、乙两名学生中产生,该班设计了一个选拔方案:甲,乙两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生甲能正确回答其中的4个问题,而学生乙能正确回答每个问题的概率均为 .甲、乙两名学生对每个问题回答正确与否都是相互独立的.
.甲、乙两名学生对每个问题回答正确与否都是相互独立的.
(1)分别求甲、乙两名学生恰好答对2个问题的概率;
(2)设甲答对的题数为 ,乙答对的题数为
,乙答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
 .甲、乙两名学生对每个问题回答正确与否都是相互独立的.
.甲、乙两名学生对每个问题回答正确与否都是相互独立的.(1)分别求甲、乙两名学生恰好答对2个问题的概率;
(2)设甲答对的题数为
 ,乙答对的题数为
,乙答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
您最近一年使用:0次
2023-11-25更新
|
1105次组卷
|
5卷引用:贵州省贵阳市五校2023届高三联合考试(四)数学(理)试题
贵州省贵阳市五校2023届高三联合考试(四)数学(理)试题辽宁省沈阳市第一二〇中学2023-2024学年高二上学期第四次质量监测数学试题(已下线)考点13 二项分布与超级几何分布 2024届高考数学考点总动员(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点1 概率统计决策问题(一)【培优版】
名校
解题方法
2 . 为回馈顾客,某商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
您最近一年使用:0次
2024-01-12更新
|
670次组卷
|
8卷引用:重庆市黔江中学校2022届高三上学期8月考试数学试题
重庆市黔江中学校2022届高三上学期8月考试数学试题(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(3)广东省广州市仲元中学2024届高三第二次调研数学试题(已下线)专题03 条件概率与全概率公式(3)(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)(已下线)第三章 随机变量及其分布列 专题二 随机变量的方差 微点2 随机变量的方差综合训练【培优版】
解题方法
3 . 根据历史资料显示,某种慢性疾病患者的自然痊愈率为5%.为试验一种新药,在有关部门批准后,医院将此药给10位病人服用,试验方案为:若这10人中至少有2人痊愈,则认为该药有效,提高了治愈率;否则,则认为该药无效.
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
您最近一年使用:0次
解题方法
4 . 为了解学生中午的用餐方式(在食堂就餐或点外卖)与最近食堂间的距离的关系,某大学于某日中午随机调查了2000名学生,获得了如下频率分布表(不完整):
并且由该频率分布表,可估计学生与最近食堂间的平均距离为 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).
(1)补全频率分布表,并根据小概率值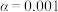 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过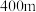 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):
(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: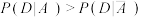 :
:
(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得 元优惠;
元优惠;
②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得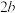 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且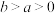 ).
).
校庆期间,已知李明每天中午去甲食堂就餐的概率均为 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
附: ,其中
,其中 .
.
学生与最近食堂间的距离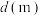 | 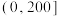 | 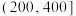 |  | 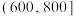 | 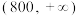 | 合计 |
| 在食堂就餐 | 0.15 | 0.10 | 0.00 | 0.50 | ||
| 点外卖 | 0.20 | 0.00 | 0.50 | |||
| 合计 | 0.20 | 0.15 | 0.00 | 1.00 |
 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).(1)补全频率分布表,并根据小概率值
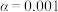 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过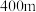 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件
 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: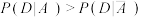 :
:(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得
 元优惠;
元优惠;②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得
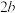 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且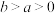 ).
).校庆期间,已知李明每天中午去甲食堂就餐的概率均为
 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.附:
 ,其中
,其中 .
. | 0.10 | 0.010 | 0.001 |
 | 2.706 | 6.635 | 10.828 |
您最近一年使用:0次
2023-12-01更新
|
940次组卷
|
9卷引用:福建省名校联盟2023届高三高考模拟考试4月数学试题
福建省名校联盟2023届高三高考模拟考试4月数学试题(已下线)重难专攻(十三) 概率与统计的综合问题 B卷素养养成卷重庆市北碚区缙云教育联盟2024届高考零诊数学试题(已下线)专题05 成对数据的统计分析压轴题(3)(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)黄金卷06(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)专题4 独立性检验压轴大题(过关集训)
5 . 学校组织A,B,C,D,E五位同学参加某大学的测试活动,现有甲、乙两种不同的测试方案,每位同学随机选择其中的一种方案进行测试,选择甲方案测试合格的概率为 ,选择乙方案测试合格的概率为
,选择乙方案测试合格的概率为 ,且每位同学测试的结果互不影响.
,且每位同学测试的结果互不影响.
(1)若5位同学全选择甲方案,将测试合格的同学的人数记为X,求X的分布列及其方差;
(2)若测试合格的人数的期望值不小于3,求选择甲方案进行测试的同学的可能人数.
 ,选择乙方案测试合格的概率为
,选择乙方案测试合格的概率为 ,且每位同学测试的结果互不影响.
,且每位同学测试的结果互不影响.(1)若5位同学全选择甲方案,将测试合格的同学的人数记为X,求X的分布列及其方差;
(2)若测试合格的人数的期望值不小于3,求选择甲方案进行测试的同学的可能人数.
您最近一年使用:0次
6 . 某校设计了一个实验学科的实验考查方案;考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2题便可通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响,求:
,且每题正确完成与否互不影响,求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
 ,且每题正确完成与否互不影响,求:
,且每题正确完成与否互不影响,求:(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
您最近一年使用:0次
2023-11-24更新
|
1246次组卷
|
6卷引用:北京市西城区北师大二附中2024届高三上学期期中数学试题
北京市西城区北师大二附中2024届高三上学期期中数学试题(已下线)模块二 专题3 概率与统计中决策问题(已下线)6.4.2超几何分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)专题7 期望方差 定义性质(经典好题母题)【练】(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点5 概率分布在生活、生产实践中的应用综合训练【培优版】
7 . 某高校设计了一个实验学科的考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作,规定至少正确完成其中
题,按照题目要求独立完成全部实验操作,规定至少正确完成其中 题才可提交通过.已知
题才可提交通过.已知 道备选题中考生甲有
道备选题中考生甲有 道题能正确完成,
道题能正确完成, 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲考生正确完成实验操作的题数的分布列,并计算均值;
(2)试从甲、乙两位考生正确完成实验操作的题数的均值、方差及至少正确完成 题的概率方面比较两位考生的实验操作能力.
题的概率方面比较两位考生的实验操作能力.
 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作,规定至少正确完成其中
题,按照题目要求独立完成全部实验操作,规定至少正确完成其中 题才可提交通过.已知
题才可提交通过.已知 道备选题中考生甲有
道备选题中考生甲有 道题能正确完成,
道题能正确完成, 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)求甲考生正确完成实验操作的题数的分布列,并计算均值;
(2)试从甲、乙两位考生正确完成实验操作的题数的均值、方差及至少正确完成
 题的概率方面比较两位考生的实验操作能力.
题的概率方面比较两位考生的实验操作能力.
您最近一年使用:0次
2023-10-31更新
|
836次组卷
|
3卷引用:湖南省邵阳市邵东创新实验学校2023-2024学年高三上学期第三次月考数学试题
湖南省邵阳市邵东创新实验学校2023-2024学年高三上学期第三次月考数学试题(已下线)6.4.1二项分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)湖南省常德市第一中学2023-2024学年高二下学期第一次月考数学试题
8 . 某职业学校为了了解毕业班学生的操作能力,设计了一个考查方案:每个考生从6道备选题中一次性随机抽取3道选题,按照题目要求正确完成,规定:至少正确完成其中2个选题方可通过.6道备选题中,考生甲有4个选题能正确完成,2个选题不能完成;考生乙每个选题正确完成的概率都是 ,且每个选题正确完成与否互不影响.
,且每个选题正确完成与否互不影响.
(1)分别求甲、乙两位考生正确完成选题个数的概率分布列(列出分布列表);
(2)请分析比较甲、乙两位考生的操作能力.
 ,且每个选题正确完成与否互不影响.
,且每个选题正确完成与否互不影响.(1)分别求甲、乙两位考生正确完成选题个数的概率分布列(列出分布列表);
(2)请分析比较甲、乙两位考生的操作能力.
您最近一年使用:0次
2023-06-16更新
|
1073次组卷
|
9卷引用:江西省萍乡市2022-2023学年高二上学期期末考试数学试题
江西省萍乡市2022-2023学年高二上学期期末考试数学试题(已下线)模块三 专题7 随机变量及其分布列--基础夯实练)(人教A版)(已下线)模块三 专题5 概率与统计--拔高能力练(人教B版)江西省宜春市宜丰县宜丰中学2022-2023学年高二创新部下学期期末考试数学试题(已下线)模块三 专题5 概率--大题分类练--基础夯实练(北师大2019版 高二)(已下线)模块一 专题7 区分超几何分布与二项分布问题黑龙江省大兴安岭实验中学(东校区)2022-2023学年高二下学期期末数学试题(已下线)专题7.4 二项分布与超几何分布【八大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(4)
解题方法
9 . 新高考数学试卷中多选题规定:在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分.在做数学卷多选题时考生通常有以下两种策略:策略A:为避免有选错得0分,在四个选项中只选出一个自己最有把握的选项,将多选题当作“单选题”来做;策略B:争取得5分,选出自己认为正确的全部选项,本次考试前,某同学通过模拟训练得出其在两种策略下作完成下面小题的情况如下表:
已知该同学作答两题的状态互不影响,若该同学此次考试决定用以下方案:第11题采用策略B,第12题采用策略A,设他这两题得分之和为X,求X的分布列、均值及方差.
策略 | 概率 | 每题耗时(分钟) | ||
第11题 | 第12题 | |||
A | 选对选项 | 0.8 | 0.5 | 3 |
B | 部分选对 | 0.6 | 0.2 | 6 |
全部选对 | 0.3 | 0.7 | ||
您最近一年使用:0次
名校
解题方法
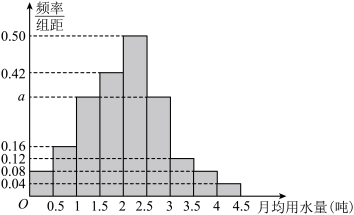
10 . 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了抽样调查,得到该市100位居民的月均用水量(单位:吨),将数据按照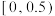 ,
, ,…,
,…,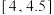 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)现从这100位居民中月均用水量在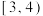 的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在
的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在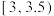 的概率;
的概率;
(2)把这100位居民的月均用水量的频率视为该市居民的月均用水量的概率,现从该市随机抽取1位,用 表示月均用水量不低于
表示月均用水量不低于 吨的人数,求
吨的人数,求 的期望和方差.
的期望和方差.
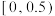 ,
, ,…,
,…,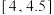 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)现从这100位居民中月均用水量在
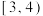 的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在
的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在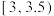 的概率;
的概率;(2)把这100位居民的月均用水量的频率视为该市居民的月均用水量的概率,现从该市随机抽取1位,用
 表示月均用水量不低于
表示月均用水量不低于 吨的人数,求
吨的人数,求 的期望和方差.
的期望和方差.
您最近一年使用:0次



