名校
解题方法
1 . 设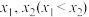 是直线
是直线 与曲线
与曲线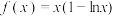 的两个交点的横坐标,则( )
的两个交点的横坐标,则( )
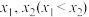 是直线
是直线 与曲线
与曲线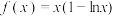 的两个交点的横坐标,则( )
的两个交点的横坐标,则( )A.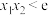 | B. |
C.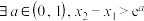 | D. |
您最近一年使用:0次
2024-06-17更新
|
462次组卷
|
2卷引用:江苏省华罗庚中学2024届高三下学期5月适应性考试数学试卷
名校
2 . 对于函数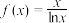 ,下列说法正确的是( )
,下列说法正确的是( )
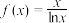 ,下列说法正确的是( )
,下列说法正确的是( )A.函数 的单调递减区间为 的单调递减区间为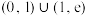 |
B. |
C.若方程 有6个不等实数根,则 有6个不等实数根,则 |
D.对任意正实数 ,且 ,且 ,若 ,若 ,则 ,则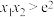 |
您最近一年使用:0次
2024-06-17更新
|
1837次组卷
|
3卷引用:湖北省武汉市2024届高三下学期5月模拟训练试题数学试卷
名校
解题方法
3 . 甲和乙两个箱子中各装有 个大小、质地均相同的小球,并且各箱中
个大小、质地均相同的小球,并且各箱中 是红球,
是红球, 是白球.
是白球.
(1)当 时,从甲箱中随机抽出2个球,求2个球的颜色不同的概率.
时,从甲箱中随机抽出2个球,求2个球的颜色不同的概率.
(2)由概率学知识可知,当总量 足够多而抽出的个体足够少时,超几何分布近似为二项分布,现从甲箱中不放回地取3个小球,恰有2个白球的概率记作
足够多而抽出的个体足够少时,超几何分布近似为二项分布,现从甲箱中不放回地取3个小球,恰有2个白球的概率记作 ;从乙箱中有放回地取3个小球,恰有2个白球的概率记作
;从乙箱中有放回地取3个小球,恰有2个白球的概率记作 .
.
①求 ,
, .
.
②当 至少为多少时,我们可以在误差不超过0.001(即
至少为多少时,我们可以在误差不超过0.001(即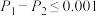 )的前提下认为超几何分布近似为二项分布?(参考数据:
)的前提下认为超几何分布近似为二项分布?(参考数据: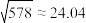 ).
).
 个大小、质地均相同的小球,并且各箱中
个大小、质地均相同的小球,并且各箱中 是红球,
是红球, 是白球.
是白球.(1)当
 时,从甲箱中随机抽出2个球,求2个球的颜色不同的概率.
时,从甲箱中随机抽出2个球,求2个球的颜色不同的概率.(2)由概率学知识可知,当总量
 足够多而抽出的个体足够少时,超几何分布近似为二项分布,现从甲箱中不放回地取3个小球,恰有2个白球的概率记作
足够多而抽出的个体足够少时,超几何分布近似为二项分布,现从甲箱中不放回地取3个小球,恰有2个白球的概率记作 ;从乙箱中有放回地取3个小球,恰有2个白球的概率记作
;从乙箱中有放回地取3个小球,恰有2个白球的概率记作 .
.①求
 ,
, .
.②当
 至少为多少时,我们可以在误差不超过0.001(即
至少为多少时,我们可以在误差不超过0.001(即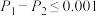 )的前提下认为超几何分布近似为二项分布?(参考数据:
)的前提下认为超几何分布近似为二项分布?(参考数据: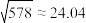 ).
).
您最近一年使用:0次
名校
4 . 设函数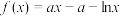 .
.
(1)讨论 的单调性;
的单调性;
(2)当 时,若
时,若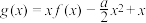 的值域为
的值域为 ,证明:
,证明: .
.
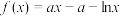 .
.(1)讨论
 的单调性;
的单调性;(2)当
 时,若
时,若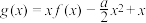 的值域为
的值域为 ,证明:
,证明: .
.
您最近一年使用:0次
名校
解题方法
5 . 已知  为坐标原点,曲线
为坐标原点,曲线  在点
在点 处的切线与曲线
处的切线与曲线  在点
在点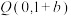 处的切线平行,且两切线间的距离为
处的切线平行,且两切线间的距离为 ,其中
,其中  .
.
(1)求实数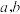 的值;
的值;
(2)若点 分别在曲线
分别在曲线 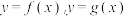 上,求
上,求  与
与 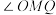 之和的最大值;
之和的最大值;
(3)若点 在曲线
在曲线  上,点
上,点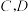 在曲线
在曲线  上,四边形
上,四边形  为正方形,其面积为
为正方形,其面积为 ,证明:
,证明: 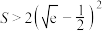
附:ln2 ≈ 0.693.
 为坐标原点,曲线
为坐标原点,曲线  在点
在点 处的切线与曲线
处的切线与曲线  在点
在点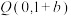 处的切线平行,且两切线间的距离为
处的切线平行,且两切线间的距离为 ,其中
,其中  .
.(1)求实数
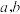 的值;
的值;(2)若点
 分别在曲线
分别在曲线 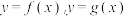 上,求
上,求  与
与 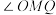 之和的最大值;
之和的最大值;(3)若点
 在曲线
在曲线  上,点
上,点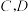 在曲线
在曲线  上,四边形
上,四边形  为正方形,其面积为
为正方形,其面积为 ,证明:
,证明: 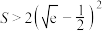
附:ln2 ≈ 0.693.
您最近一年使用:0次
2024-06-16更新
|
312次组卷
|
2卷引用:山东省青岛市2024届高三第三次适应性检测数学试题
解题方法
6 . 已知函数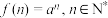 .
.
①当 时,
时,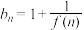 ,记
,记 前
前 项积为
项积为 ,若
,若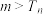 恒成立,整数
恒成立,整数 的最小值是
的最小值是______________ ;
②对所有n都有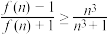 成立,则
成立,则 的最小值是
的最小值是_____________ .
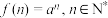 .
.①当
 时,
时,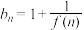 ,记
,记 前
前 项积为
项积为 ,若
,若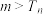 恒成立,整数
恒成立,整数 的最小值是
的最小值是②对所有n都有
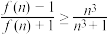 成立,则
成立,则 的最小值是
的最小值是
您最近一年使用:0次
名校
解题方法
7 . 已知 ,
, 分别是函数
分别是函数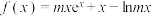 和
和 图象上的动点,若对任意的
图象上的动点,若对任意的 ,都有
,都有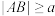 恒成立,则实数a的最大值为
恒成立,则实数a的最大值为______ .
 ,
, 分别是函数
分别是函数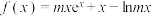 和
和 图象上的动点,若对任意的
图象上的动点,若对任意的 ,都有
,都有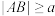 恒成立,则实数a的最大值为
恒成立,则实数a的最大值为
您最近一年使用:0次
2024-06-16更新
|
306次组卷
|
3卷引用:广东省东莞中学、广州二中、惠州一中、深圳实验、珠海一中、中山纪念中学2024届高三下学期第五次六校联考数学试题
8 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点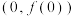 处的切线方程;
处的切线方程;
(2)若函数 ,求证:
,求证: .
.
 .
.(1)当
 时,求曲线
时,求曲线 在点
在点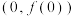 处的切线方程;
处的切线方程;(2)若函数
 ,求证:
,求证: .
.
您最近一年使用:0次
解题方法
9 . 已知函数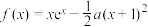 .则下列说法中错误的是( )
.则下列说法中错误的是( )
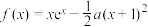 .则下列说法中错误的是( )
.则下列说法中错误的是( )A.当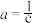 时, 时, 在 在 上单调递增 上单调递增 |
B.当 时, 时, 的最小值是一个与 的最小值是一个与 无关的常数 无关的常数 |
C. 可能有三个不同的零点 可能有三个不同的零点 |
D.当 时, 时, 有且仅有一个零点 有且仅有一个零点 |
您最近一年使用:0次
2024-06-15更新
|
278次组卷
|
2卷引用:江西省南昌市2024届高三第三次模拟测试数学试题
名校
10 . 定义:若变量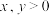 ,且满足:
,且满足: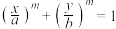 ,其中
,其中 ,称
,称 是关于的“
是关于的“ 型函数”.
型函数”.
(1)当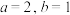 时,求
时,求 关于
关于 的“2型函数”在点
的“2型函数”在点 处的切线方程;
处的切线方程;
(2)若 是关于
是关于 的“
的“ 型函数”,
型函数”,
(i)求 的最小值:
的最小值:
(ii)求证: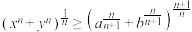 ,
,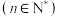 .
.
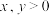 ,且满足:
,且满足: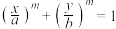 ,其中
,其中 ,称
,称 是关于的“
是关于的“ 型函数”.
型函数”.(1)当
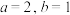 时,求
时,求 关于
关于 的“2型函数”在点
的“2型函数”在点 处的切线方程;
处的切线方程;(2)若
 是关于
是关于 的“
的“ 型函数”,
型函数”,(i)求
 的最小值:
的最小值:(ii)求证:
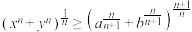 ,
,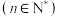 .
.
您最近一年使用:0次
2024-06-15更新
|
286次组卷
|
3卷引用:江西省南昌市2024届高三第三次模拟测试数学试题



