1 . 已知数列 满足
满足 ,
, .
.
(1)证明:数列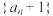 为等比数列;
为等比数列;
(2)在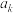 与
与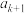 之间插入
之间插入 个数,使得这
个数,使得这 个数组成公差为
个数组成公差为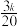 的等差数列,求
的等差数列,求 .
.
 满足
满足 ,
, .
.(1)证明:数列
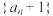 为等比数列;
为等比数列;(2)在
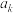 与
与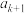 之间插入
之间插入 个数,使得这
个数,使得这 个数组成公差为
个数组成公差为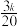 的等差数列,求
的等差数列,求 .
.
您最近一年使用:0次
2024-05-28更新
|
714次组卷
|
6卷引用:山西省临汾市部分学校2023-2024学年高二下学期5月质量检测数学试题
名校
解题方法
2 . 设数列 的前
的前 项和为
项和为 ,已知
,已知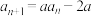 ,则下列结论正确的为( )
,则下列结论正确的为( )
 的前
的前 项和为
项和为 ,已知
,已知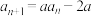 ,则下列结论正确的为( )
,则下列结论正确的为( )A.若 ,则 ,则 为等差数列 为等差数列 | B.若 ,则 ,则 |
C.若 ,则 ,则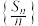 是公差为 是公差为 的等差数列 的等差数列 | D.若 ,则 ,则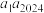 的最大值为1 的最大值为1 |
您最近一年使用:0次
2024-05-28更新
|
429次组卷
|
6卷引用:山西省临汾市部分学校2023-2024学年高二下学期5月质量检测数学试题
解题方法
3 . 已知等差数列 的前n项和为
的前n项和为 ,等比数列
,等比数列 的前n项和为
的前n项和为 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的前n项和为
的前n项和为 ,等比数列
,等比数列 的前n项和为
的前n项和为 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若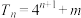 ,则 ,则 |
B.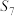 , , , , 成等差数列 成等差数列 |
C.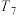 , , , , 成等比数列 成等比数列 |
D.若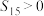 , ,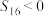 ,则使得 ,则使得 取得最大值的正整数n的值为8 取得最大值的正整数n的值为8 |
您最近一年使用:0次
4 . 已知数列 的前
的前 项和为
项和为 ,
,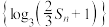 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
(1)求 的通项公式;
的通项公式;
(2)设数列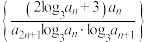 的前
的前 项和为
项和为 ,证明:
,证明: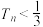 .
.
 的前
的前 项和为
项和为 ,
,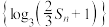 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.(1)求
 的通项公式;
的通项公式;(2)设数列
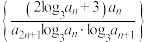 的前
的前 项和为
项和为 ,证明:
,证明: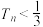 .
.
您最近一年使用:0次
5 . 某公司计划在10年内每年某产品的销售额(单位:万元)等于上一年的1.2倍再减去2.已知第一年(2023年)该公司该产品的销售额为100万元,则按照计划该公司从2023年到2032年该产品的销售总额约为(参考数据: )( )
)( )
 )( )
)( )| A.2135.5万元 | B.2235.5万元 | C.2335.5万元 | D.2435.5万元 |
您最近一年使用:0次
名校
6 . 已知等比数列 的前
的前 项和
项和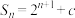 ,若
,若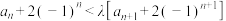 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
 的前
的前 项和
项和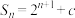 ,若
,若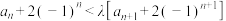 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )A. | B.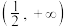 |
C. | D. |
您最近一年使用:0次
2023-11-29更新
|
500次组卷
|
2卷引用:山西省临汾市2023-2024学年高三上学期11月期中数学试题
7 . 记正项数列 的前
的前 项和为
项和为 ,已知
,已知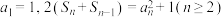 .
.
(1)求 ;
;
(2)若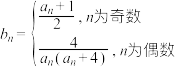 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求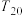 的值.
的值.
 的前
的前 项和为
项和为 ,已知
,已知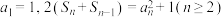 .
.(1)求
 ;
;(2)若
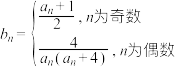 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求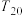 的值.
的值.
您最近一年使用:0次
2023-11-27更新
|
770次组卷
|
3卷引用:山西省临汾市2023-2024学年高三上学期11月期中数学试题
解题方法
8 . 数列 的前
的前 项和为
项和为 ,且
,且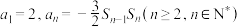 .
.
(1)求 ;
;
(2)若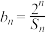 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且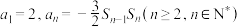 .
.(1)求
 ;
;(2)若
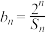 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
解题方法
9 . 已知数列 的前
的前 项和为
项和为 ,则( )
,则( )
 的前
的前 项和为
项和为 ,则( )
,则( )A.若 ,则 ,则 是等差数列 是等差数列 |
B.若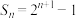 ,则 ,则 是等比数列 是等比数列 |
C.若 是等差数列,则 是等差数列,则 |
D.若 是等比数列,且 是等比数列,且 , , ,则 ,则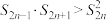 |
您最近一年使用:0次
2022-11-27更新
|
813次组卷
|
4卷引用:山西省临汾市2023届高三上学期11月月考数学试题
山西省临汾市2023届高三上学期11月月考数学试题安徽省九师联盟2022-2023学年高三上学期11月质量检测数学试题(已下线)专题04 数列的通项、求和及综合应用(精讲精练)-4福建省南安市柳城中学2022-2023学年高三上学期12月月考数学试题
10 . 在各项均为正数的等比数列 中,
中, 为其前n项和,
为其前n项和, ,
, ,
, ,
, 成等差数列.
成等差数列.
(1)求 的通项公式;
的通项公式;
(2)若 ,数列
,数列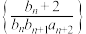 的前n项和为
的前n项和为 ,证明:
,证明: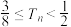 .
.
 中,
中, 为其前n项和,
为其前n项和, ,
, ,
, ,
, 成等差数列.
成等差数列.(1)求
 的通项公式;
的通项公式;(2)若
 ,数列
,数列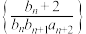 的前n项和为
的前n项和为 ,证明:
,证明: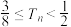 .
.
您最近一年使用:0次
2022-11-26更新
|
1045次组卷
|
5卷引用:山西省临汾市2023届高三上学期11月月考数学试题



