1 . 在平面直角坐标系 中,点
中,点 ,
,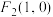 ,
,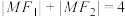 ,点M的轨迹为C.
,点M的轨迹为C.

(1)求C的方程:
(2)设点P在直线 上,过点P的两条直线分别交C于A,B两点和G,H两点,若直线AB与直线GH的斜率之和为0,证明:
上,过点P的两条直线分别交C于A,B两点和G,H两点,若直线AB与直线GH的斜率之和为0,证明: .
.
 中,点
中,点 ,
,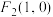 ,
,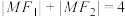 ,点M的轨迹为C.
,点M的轨迹为C.
(1)求C的方程:
(2)设点P在直线
 上,过点P的两条直线分别交C于A,B两点和G,H两点,若直线AB与直线GH的斜率之和为0,证明:
上,过点P的两条直线分别交C于A,B两点和G,H两点,若直线AB与直线GH的斜率之和为0,证明: .
.
您最近一年使用:0次
名校
解题方法
2 . 如图,已知椭圆 的左、右焦点分别为
的左、右焦点分别为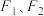 ,
,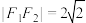 ,设
,设 是第一象限内椭圆C上的一点,
是第一象限内椭圆C上的一点, 的延长线分别交椭圆C于点
的延长线分别交椭圆C于点 .当
.当 时,
时,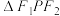 的面积为
的面积为 .
.

(1)求椭圆C的方程;
(2)分别记 和
和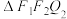 的面积为
的面积为 和
和 ,求
,求 的最大值.
的最大值.
 的左、右焦点分别为
的左、右焦点分别为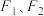 ,
,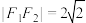 ,设
,设 是第一象限内椭圆C上的一点,
是第一象限内椭圆C上的一点, 的延长线分别交椭圆C于点
的延长线分别交椭圆C于点 .当
.当 时,
时,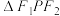 的面积为
的面积为 .
.
(1)求椭圆C的方程;
(2)分别记
 和
和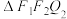 的面积为
的面积为 和
和 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2022-06-13更新
|
1749次组卷
|
5卷引用:浙江省温州市平阳县万全综合高级中学2022-2023学年高二下学期第一次月考数学试题
名校
解题方法
3 . 若曲线C的方程为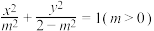 ,则( )
,则( )
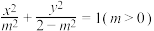 ,则( )
,则( )A.当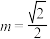 时,曲线C表示椭圆,离心率为 时,曲线C表示椭圆,离心率为 |
B.当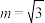 时,曲线C表示双曲线,渐近线方程为 时,曲线C表示双曲线,渐近线方程为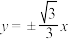 |
C.当 时,曲线C表示圆,半径为1 时,曲线C表示圆,半径为1 |
| D.当曲线C表示椭圆时,焦距的最大值为4 |
您最近一年使用:0次
2022-06-13更新
|
1711次组卷
|
6卷引用:浙江省温州市平阳县万全综合高级中学2022-2023学年高二下学期第一次月考数学试题
4 . 如果点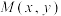 在运动过程中,总满足关系式
在运动过程中,总满足关系式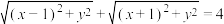 ,记满足此条件的点M的轨迹为C,直线
,记满足此条件的点M的轨迹为C,直线 与C交于D,E,已知
与C交于D,E,已知 ,则
,则 周长的最大值为
周长的最大值为______ .
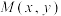 在运动过程中,总满足关系式
在运动过程中,总满足关系式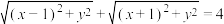 ,记满足此条件的点M的轨迹为C,直线
,记满足此条件的点M的轨迹为C,直线 与C交于D,E,已知
与C交于D,E,已知 ,则
,则 周长的最大值为
周长的最大值为
您最近一年使用:0次
2022-02-13更新
|
490次组卷
|
4卷引用:浙江省温州市瑞安市第六中学2021-2022学年高二下学期入学检测数学试题 .
解题方法
5 . 已知椭圆 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,过
,过 的直线交椭圆E于A,B两点.当
的直线交椭圆E于A,B两点.当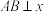 轴时,
轴时, .
.
(1)求椭圆E的方程;
(2)求 的范围.
的范围.
 的离心率为
的离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,过
,过 的直线交椭圆E于A,B两点.当
的直线交椭圆E于A,B两点.当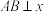 轴时,
轴时, .
.(1)求椭圆E的方程;
(2)求
 的范围.
的范围.
您最近一年使用:0次
2022-02-13更新
|
363次组卷
|
4卷引用:浙江省温州市瑞安市第六中学2021-2022学年高二下学期入学检测数学试题 .
浙江省温州市瑞安市第六中学2021-2022学年高二下学期入学检测数学试题 .山东省菏泽市2021-2022学年高二上学期期末数学试题(已下线)第5课时 课后 双曲线的几何性质(已下线)第2课时 课后 椭圆的几何性质
名校
解题方法
6 . 已知椭圆 的离心率为
的离心率为 ,且过点
,且过点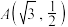 .
.
(1)求椭圆的方程;
(2)直线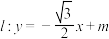 与椭圆交于B,C两点,若
与椭圆交于B,C两点,若 面积为
面积为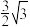 ,求m.
,求m.
 的离心率为
的离心率为 ,且过点
,且过点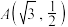 .
.(1)求椭圆的方程;
(2)直线
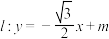 与椭圆交于B,C两点,若
与椭圆交于B,C两点,若 面积为
面积为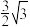 ,求m.
,求m.
您最近一年使用:0次
2022-01-21更新
|
883次组卷
|
3卷引用:浙江省温州市2021-2022学年高二上学期期末教学质量统一检测数学试题(A卷)
名校
解题方法
7 . 在平面直角坐标系 中,已知点
中,已知点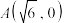 ,
, ,过点
,过点 的动直线
的动直线 与过点
与过点 的动直线
的动直线 的交点为P,
的交点为P, ,
, 的斜率均存在且乘积为
的斜率均存在且乘积为 ,设动点Р的轨迹为曲线C.
,设动点Р的轨迹为曲线C.
(1)求曲线C的方程;
(2)若点M在曲线C上,过点M且垂直于OM的直线交C于另一点N,点M关于原点O的对称点为Q.直线NQ交x轴于点T,求 的最大值.
的最大值.
 中,已知点
中,已知点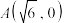 ,
, ,过点
,过点 的动直线
的动直线 与过点
与过点 的动直线
的动直线 的交点为P,
的交点为P, ,
, 的斜率均存在且乘积为
的斜率均存在且乘积为 ,设动点Р的轨迹为曲线C.
,设动点Р的轨迹为曲线C.(1)求曲线C的方程;
(2)若点M在曲线C上,过点M且垂直于OM的直线交C于另一点N,点M关于原点O的对称点为Q.直线NQ交x轴于点T,求
 的最大值.
的最大值.
您最近一年使用:0次
2022-01-12更新
|
821次组卷
|
5卷引用:浙江省温州市瑞安中学2021-2022学年高二下学期期初测试数学试题
浙江省温州市瑞安中学2021-2022学年高二下学期期初测试数学试题重庆市2021-2022学年高二上学期期末数学试题(已下线)解密14 椭圆及其方程(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)(已下线)2022年高考浙江数学高考真题变式题13-15题(已下线)2022年高考浙江数学高考真题变式题19-22题
解题方法
8 . 已知椭圆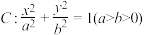 的左右焦点分别为
的左右焦点分别为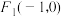 ,
, .过
.过 与
与 轴垂直的直线与椭圆
轴垂直的直线与椭圆 交于点
交于点 ,点
,点 在
在 轴上方,且
轴上方,且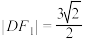 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,是否存在一定点
两点,是否存在一定点 使得
使得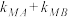 为定值,若存在,求出点
为定值,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
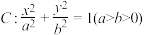 的左右焦点分别为
的左右焦点分别为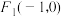 ,
, .过
.过 与
与 轴垂直的直线与椭圆
轴垂直的直线与椭圆 交于点
交于点 ,点
,点 在
在 轴上方,且
轴上方,且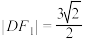 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,是否存在一定点
两点,是否存在一定点 使得
使得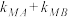 为定值,若存在,求出点
为定值,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
您最近一年使用:0次
2022-01-03更新
|
572次组卷
|
2卷引用:浙江省温州市环大罗山联盟2022-2023学年高二上学期期中联考数学试题
名校
解题方法
9 . 已知 是平面上的动点, 且点
是平面上的动点, 且点 与
与 的距离之和为
的距离之和为 .点
.点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)不与 轴垂直的直线
轴垂直的直线 过点
过点 且交曲线
且交曲线 于
于 两点, 曲线
两点, 曲线 与
与 轴的交点为
轴的交点为 ,当
,当 时,求
时,求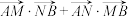 的取值范围.
的取值范围.
 是平面上的动点, 且点
是平面上的动点, 且点 与
与 的距离之和为
的距离之和为 .点
.点 的轨迹为曲线
的轨迹为曲线 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)不与
 轴垂直的直线
轴垂直的直线 过点
过点 且交曲线
且交曲线 于
于 两点, 曲线
两点, 曲线 与
与 轴的交点为
轴的交点为 ,当
,当 时,求
时,求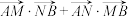 的取值范围.
的取值范围.
您最近一年使用:0次
2021-11-23更新
|
947次组卷
|
6卷引用:浙江省温州市十校联合体2021-2022学年高二上学期期中联考数学试题
浙江省温州市十校联合体2021-2022学年高二上学期期中联考数学试题浙江省温州市瑞安市第六中学2021-2022学年高二上学期12月月考数学试题浙江省台州市玉环市玉城中学2021-2022学年高二上学期期中数学试题(已下线)高二上学期期中【易错60题考点专练】(选修一全部内容)-2022-2023学年高二数学考试满分全攻略(人教A版2019选修第一册)(已下线)专题28 圆锥曲线求范围及最值六种类型大题100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)湖北省武汉市硚口区2022届高三下学期5月训练数学试题
10 . 椭圆 ,已知
,已知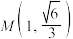 、
、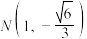 、
、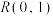 、
、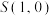 中恰有三个点在椭圆
中恰有三个点在椭圆 上,圆
上,圆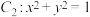 的切线
的切线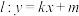 与椭圆
与椭圆 相交于
相交于 、
、 两点,与
两点,与 轴交于点
轴交于点 ,
, 和
和 的面积分别为
的面积分别为 和
和 .(O是坐标原点)
.(O是坐标原点)
(1)求椭圆 的标准方程;
的标准方程;
(2)若 ,求
,求 的取值范围.
的取值范围.
 ,已知
,已知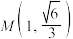 、
、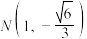 、
、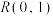 、
、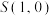 中恰有三个点在椭圆
中恰有三个点在椭圆 上,圆
上,圆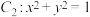 的切线
的切线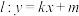 与椭圆
与椭圆 相交于
相交于 、
、 两点,与
两点,与 轴交于点
轴交于点 ,
, 和
和 的面积分别为
的面积分别为 和
和 .(O是坐标原点)
.(O是坐标原点)(1)求椭圆
 的标准方程;
的标准方程;(2)若
 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次



