解题方法
1 . 在等差数列 中,
中,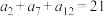 ,则
,则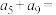 ( )
( )
 中,
中,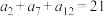 ,则
,则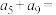 ( )
( )| A.7 | B.11 | C.14 | D.16 |
您最近一年使用:0次
解题方法
2 . 递增等比数列 中,
中, ,
,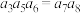 ,则
,则 ( )
( )
 中,
中, ,
,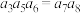 ,则
,则 ( )
( )A. | B. | C.72 | D.144 |
您最近一年使用:0次
3 . 如果数列 满足:
满足: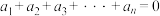 且
且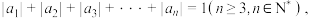 则称
则称 为n阶“归化”数列.
为n阶“归化”数列.
(1)若某3阶“归化”数列 是等差数列,且单调递增,写出该数列的各项;
是等差数列,且单调递增,写出该数列的各项;
(2)若某11阶“归化”数列 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;
(3)若 为n阶“归化”数列,求证
为n阶“归化”数列,求证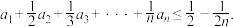
 满足:
满足: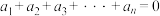 且
且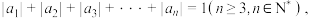 则称
则称 为n阶“归化”数列.
为n阶“归化”数列.(1)若某3阶“归化”数列
 是等差数列,且单调递增,写出该数列的各项;
是等差数列,且单调递增,写出该数列的各项;(2)若某11阶“归化”数列
 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;(3)若
 为n阶“归化”数列,求证
为n阶“归化”数列,求证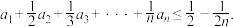
您最近一年使用:0次
解题方法
4 . 设等比数列 的前n项和为
的前n项和为 ,则“
,则“ 是递增数列”是“
是递增数列”是“ 是递增数列”的( )
是递增数列”的( )
 的前n项和为
的前n项和为 ,则“
,则“ 是递增数列”是“
是递增数列”是“ 是递增数列”的( )
是递增数列”的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
5 . 已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为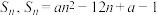 ,则( )
,则( )
 的公差为
的公差为 ,前
,前 项和为
项和为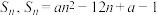 ,则( )
,则( )A. | B. |
C. | D.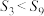 |
您最近一年使用:0次
解题方法
6 . 《九章算术》是我国古代数学名著,其中记载了关于家畜偷吃禾苗的问题.假设有羊、骡子、马、牛吃了别人的禾苗,禾苗的主人要求羊的主人、骡子的主人、马的主人、牛的主人共赔偿12斗粟.羊的主人说:“羊吃得最少,羊和骡子吃的禾苗总数只有马和牛吃的禾苗总数的一半.”骡子的主人说:“骡子吃的禾苗只有羊和马吃的禾苗总数的一半.”马的主人说:“马吃的禾苗只有骡子和牛吃的禾苗总数的一半.”若按照此比率偿还,则羊的主人应赔偿的粟的斗数为( )
| A.1 | B. | C.2 | D. |
您最近一年使用:0次
2024-07-19更新
|
168次组卷
|
4卷引用:湖南省湘西州2023-2024学年高二下学期期末考试数学试卷
解题方法
7 . 已知数列 的前
的前 项和为
项和为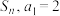 ,且
,且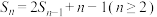 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
 的前
的前 项和为
项和为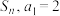 ,且
,且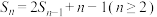 ,则下列结论中正确的是( )
,则下列结论中正确的是( )A.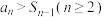 | B.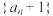 是等比数列 是等比数列 |
C.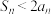 | D.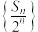 是递增数列 是递增数列 |
您最近一年使用:0次
名校
解题方法
8 . 已知数列 的前
的前 项和
项和 ,且满足
,且满足 .
.
(1)求 的通项公式;
的通项公式;
(2)记数列 的前
的前 项乘积为
项乘积为 ,求
,求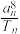 的最小值.
的最小值.
 的前
的前 项和
项和 ,且满足
,且满足 .
.(1)求
 的通项公式;
的通项公式;(2)记数列
 的前
的前 项乘积为
项乘积为 ,求
,求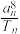 的最小值.
的最小值.
您最近一年使用:0次
2024-07-18更新
|
476次组卷
|
4卷引用:十五校教育集团鄂豫皖三十八校2023-2024学年高二6月阶段联考数学试题
十五校教育集团鄂豫皖三十八校2023-2024学年高二6月阶段联考数学试题(已下线)专题22 类比与结构思想解等比数列问题(一题多变)河南省部分学校2025届高三7月联合质量检测数学试题(已下线)5.3 递推公式求数列通项公式(讲义)
9 . 记 为等差数列
为等差数列 的前n项和,已知
的前n项和,已知

(1)求 的通项公式;
的通项公式;
(2)记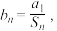 求证:数列
求证:数列 的前
的前 项和
项和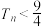

 为等差数列
为等差数列 的前n项和,已知
的前n项和,已知

(1)求
 的通项公式;
的通项公式;(2)记
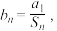 求证:数列
求证:数列 的前
的前 项和
项和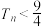

您最近一年使用:0次
10 . 已知数列 满足
满足 ,
, ,数列
,数列 是正项等比数列,且
是正项等比数列,且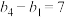 ,
, .
.
(1)求 ,
, 的通项公式;
的通项公式;
(2)从下面①②两个条件中选择一个作为已知条件,求数列 的前
的前 项和
项和 .
.
①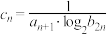 ;②
;② .
.
 满足
满足 ,
, ,数列
,数列 是正项等比数列,且
是正项等比数列,且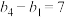 ,
, .
.(1)求
 ,
, 的通项公式;
的通项公式;(2)从下面①②两个条件中选择一个作为已知条件,求数列
 的前
的前 项和
项和 .
.①
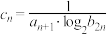 ;②
;② .
.
您最近一年使用:0次



