1 . 如图,在四棱锥 中,四边形
中,四边形 是边长为2的菱形,
是边长为2的菱形, ,
, 为正三角形,
为正三角形, ,
, 分别为
分别为 ,
,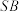 的中点.
的中点.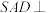 平面
平面 ,求直线
,求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(2)求证:平面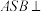 平面
平面 .
.
 中,四边形
中,四边形 是边长为2的菱形,
是边长为2的菱形, ,
, 为正三角形,
为正三角形, ,
, 分别为
分别为 ,
,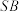 的中点.
的中点.
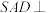 平面
平面 ,求直线
,求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;(2)求证:平面
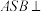 平面
平面 .
.
您最近一年使用:0次
名校
解题方法
2 . 在四棱锥 中,四边形
中,四边形 为矩形,
为矩形, 平面
平面 ,则下列结论正确的是( )
,则下列结论正确的是( )
 中,四边形
中,四边形 为矩形,
为矩形, 平面
平面 ,则下列结论正确的是( )
,则下列结论正确的是( )A.平面 与平面 与平面 垂直 垂直 |
B. 为钝角三角形 为钝角三角形 |
C.平面 与平面 与平面 垂直 垂直 |
D. |
您最近一年使用:0次
3 . 如图,菱形 的对角线
的对角线 与
与 交于点
交于点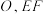 是
是 的中位线,
的中位线, 与
与 交于点
交于点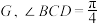 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形,且
旋转过程中的一个图形,且 平面
平面 .则下列结论中正确的是( )
.则下列结论中正确的是( )
 的对角线
的对角线 与
与 交于点
交于点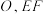 是
是 的中位线,
的中位线, 与
与 交于点
交于点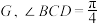 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形,且
旋转过程中的一个图形,且 平面
平面 .则下列结论中正确的是( )
.则下列结论中正确的是( )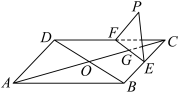
A.异面直线 与 与 的夹角为 的夹角为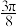 |
B.平面 平面 平面 |
C. 与 与 可能垂直 可能垂直 |
D. 与 与 可能平行 可能平行 |
您最近一年使用:0次
4 . 图1所示的是等腰梯形ABCD,AB//CD,AB=3,CD=1,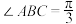 ,DE⊥AB于E点,现将△ADE沿直线DE折起到△PDE的位置,连接PB,PC,形成一个四棱锥P-EBCD,如图2所示.
,DE⊥AB于E点,现将△ADE沿直线DE折起到△PDE的位置,连接PB,PC,形成一个四棱锥P-EBCD,如图2所示.
(2)求证:平面PBE⊥平面BCDE;
(3)若二面角P-ED-B的大小为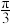 ,求三棱锥E-PCD的体积
,求三棱锥E-PCD的体积
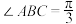 ,DE⊥AB于E点,现将△ADE沿直线DE折起到△PDE的位置,连接PB,PC,形成一个四棱锥P-EBCD,如图2所示.
,DE⊥AB于E点,现将△ADE沿直线DE折起到△PDE的位置,连接PB,PC,形成一个四棱锥P-EBCD,如图2所示.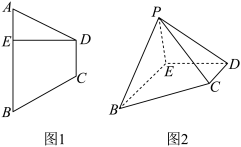
(2)求证:平面PBE⊥平面BCDE;
(3)若二面角P-ED-B的大小为
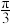 ,求三棱锥E-PCD的体积
,求三棱锥E-PCD的体积
您最近一年使用:0次
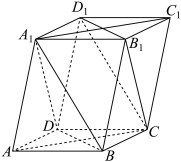
5 . 如图,四棱柱 的底面
的底面 是正方形,
是正方形, .
.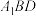 ∥平面
∥平面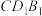 ;
;
(2)证明:平面 平面
平面 .
.
 的底面
的底面 是正方形,
是正方形, .
.
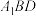 ∥平面
∥平面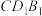 ;
;(2)证明:平面
 平面
平面 .
.
您最近一年使用:0次
7日内更新
|
605次组卷
|
4卷引用:河北省廊坊市多校联考2023-2024学年高一下学期7月期末质量检测数学试卷
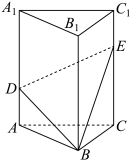
6 . 如图,在正三棱柱 中,点
中,点 ,
, 分别在
分别在 ,
, 上,
上,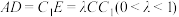 ,记正三棱柱
,记正三棱柱 的体积为
的体积为 .
.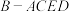 的体积(结果用
的体积(结果用 表示);
表示);
(2)当 时,
时,
①请在图中直接画出平面 与平面
与平面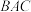 的交线;(不写过程,保留作图痕迹)
的交线;(不写过程,保留作图痕迹)
②求证:平面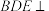 平面
平面 .
.
 中,点
中,点 ,
, 分别在
分别在 ,
, 上,
上,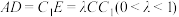 ,记正三棱柱
,记正三棱柱 的体积为
的体积为 .
.
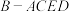 的体积(结果用
的体积(结果用 表示);
表示);(2)当
 时,
时,①请在图中直接画出平面
 与平面
与平面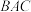 的交线;(不写过程,保留作图痕迹)
的交线;(不写过程,保留作图痕迹)②求证:平面
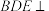 平面
平面 .
.
您最近一年使用:0次
解题方法
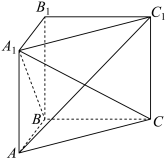
7 . 如图,在直三棱柱 中,
中, ,
, .
. 平面
平面 ;
;
(2)求证: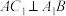 .
.
 中,
中, ,
, .
.
 平面
平面 ;
;(2)求证:
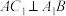 .
.
您最近一年使用:0次
8 . 如图,已知菱形 的边长为4,
的边长为4,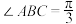 ,
, 平面
平面 ,
, ,E,F分别为BC,CD的中点,AC交EF于点G.
,E,F分别为BC,CD的中点,AC交EF于点G.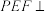 平面
平面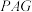 ;
;
(2)求点B到平面PEF的距离.
 的边长为4,
的边长为4,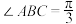 ,
, 平面
平面 ,
, ,E,F分别为BC,CD的中点,AC交EF于点G.
,E,F分别为BC,CD的中点,AC交EF于点G.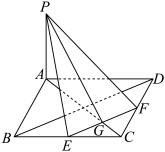
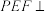 平面
平面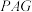 ;
;(2)求点B到平面PEF的距离.
您最近一年使用:0次
9 . 如图,在矩形 中,
中,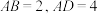 ,
, 是
是 的中点,将
的中点,将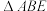 沿
沿 折起使点
折起使点 到点
到点 的位置,
的位置, 是
是 的中点.
的中点.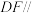 平面
平面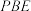 ;
;
(2)若 ,证明:平面
,证明:平面 平面
平面 ;
;
(3)在(2)的条件下,求二面角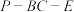 的余弦值.
的余弦值.
 中,
中,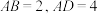 ,
, 是
是 的中点,将
的中点,将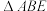 沿
沿 折起使点
折起使点 到点
到点 的位置,
的位置, 是
是 的中点.
的中点.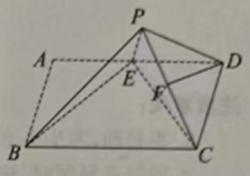
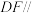 平面
平面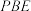 ;
;(2)若
 ,证明:平面
,证明:平面 平面
平面 ;
;(3)在(2)的条件下,求二面角
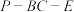 的余弦值.
的余弦值.
您最近一年使用:0次
10 . 如图,在三棱锥 中,
中, 是等边三角形,
是等边三角形, 分别为
分别为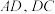 的中点.
的中点.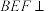 平面
平面 ;
;
(2)求二面角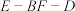 的余弦值.
的余弦值.
 中,
中, 是等边三角形,
是等边三角形, 分别为
分别为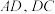 的中点.
的中点.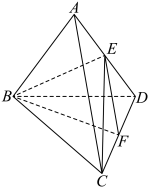
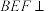 平面
平面 ;
;(2)求二面角
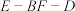 的余弦值.
的余弦值.
您最近一年使用:0次



