1 . 在一场乒乓球赛中,甲、乙、丙、丁四人角逐冠军.比赛采用“双败淘汰制”,具体赛制为:首先四人抽签两两对阵,胜者进入“胜区”,败者进入“败区”;接下来,“胜区”的两人对阵,胜者进入最后决赛;“败区”的两个对阵,败者直接淘汰出局并获得第四名;紧接着“败区”的胜者和“胜区”的“败者”对阵,胜者晋级到最后的决赛,败者获得第三名:最后,剩下的两人进行最后的冠军决赛,胜者获得冠军,败者获得第二名.甲对阵乙、丙、丁获胜的概率均为 ,且不同对阵结果相互独立.
,且不同对阵结果相互独立.
(1)若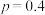 ,第一轮由甲对阵乙,丙对阵丁.
,第一轮由甲对阵乙,丙对阵丁.
①求甲获得第四名的概率;
②求甲在“双败淘汰制”下参与对阵的比赛场数的数学期望.
(2)除“双败淘汰制”外,也经常采用“单败淘汰制”:四人抽签决定两两对阵,两场比赛的胜者晋级到冠军决赛,败者参加三、四名比赛,哪种赛制对甲夺冠有利?请说明理由.
 ,且不同对阵结果相互独立.
,且不同对阵结果相互独立.(1)若
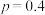 ,第一轮由甲对阵乙,丙对阵丁.
,第一轮由甲对阵乙,丙对阵丁.①求甲获得第四名的概率;
②求甲在“双败淘汰制”下参与对阵的比赛场数的数学期望.
(2)除“双败淘汰制”外,也经常采用“单败淘汰制”:四人抽签决定两两对阵,两场比赛的胜者晋级到冠军决赛,败者参加三、四名比赛,哪种赛制对甲夺冠有利?请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 某疫苗生产单位通过验血的方式检验某种疫苗产生抗体情况,现有 份血液样本(数量足够大),有以下两种检验方式:
份血液样本(数量足够大),有以下两种检验方式:
方式一:逐份检验,需要检验 次;
次;
方式二:混合检验,将其中 份血液样本混合检验,若混合血样无抗体,说明这
份血液样本混合检验,若混合血样无抗体,说明这 份血液样本全无抗体,只需检验1次;若混合血样有抗体,为了明确具体哪份血液样本有抗体,需要对每份血液样本再分别化验一次,检验总次数为
份血液样本全无抗体,只需检验1次;若混合血样有抗体,为了明确具体哪份血液样本有抗体,需要对每份血液样本再分别化验一次,检验总次数为 次.假设每份样本的检验结果相互独立,每份样本有抗体的概率均为
次.假设每份样本的检验结果相互独立,每份样本有抗体的概率均为 .
.
(1)现有5份不同的血液样本,其中只有2份血液样本有抗体,采用逐份检验方式,求恰好经过3次检验就能把有抗体的血液样本全部检验出来的概率;
(2)现取其中 份血液样本,记采用逐份检验方式,样本需要检验的总次数为
份血液样本,记采用逐份检验方式,样本需要检验的总次数为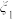 ;采用混合检验方式,样本需要检验的总次数为
;采用混合检验方式,样本需要检验的总次数为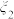 .
.
①若 ,求
,求 关于
关于 的函数关系式
的函数关系式 ;
;
②已知 ,以检验总次数的期望为依据,讨论采用何种检验方式更好?
,以检验总次数的期望为依据,讨论采用何种检验方式更好?
参考数据: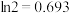 ,
,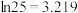 ,
,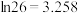 ,
, ,
,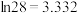 .
.
 份血液样本(数量足够大),有以下两种检验方式:
份血液样本(数量足够大),有以下两种检验方式:方式一:逐份检验,需要检验
 次;
次;方式二:混合检验,将其中
 份血液样本混合检验,若混合血样无抗体,说明这
份血液样本混合检验,若混合血样无抗体,说明这 份血液样本全无抗体,只需检验1次;若混合血样有抗体,为了明确具体哪份血液样本有抗体,需要对每份血液样本再分别化验一次,检验总次数为
份血液样本全无抗体,只需检验1次;若混合血样有抗体,为了明确具体哪份血液样本有抗体,需要对每份血液样本再分别化验一次,检验总次数为 次.假设每份样本的检验结果相互独立,每份样本有抗体的概率均为
次.假设每份样本的检验结果相互独立,每份样本有抗体的概率均为 .
.(1)现有5份不同的血液样本,其中只有2份血液样本有抗体,采用逐份检验方式,求恰好经过3次检验就能把有抗体的血液样本全部检验出来的概率;
(2)现取其中
 份血液样本,记采用逐份检验方式,样本需要检验的总次数为
份血液样本,记采用逐份检验方式,样本需要检验的总次数为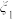 ;采用混合检验方式,样本需要检验的总次数为
;采用混合检验方式,样本需要检验的总次数为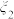 .
.①若
 ,求
,求 关于
关于 的函数关系式
的函数关系式 ;
;②已知
 ,以检验总次数的期望为依据,讨论采用何种检验方式更好?
,以检验总次数的期望为依据,讨论采用何种检验方式更好?参考数据:
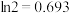 ,
,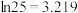 ,
,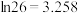 ,
, ,
,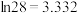 .
.
您最近一年使用:0次
7日内更新
|
266次组卷
|
3卷引用:湖北省武汉市5G联合体2023-2024学年高二下学期期末考试数学试卷
湖北省武汉市5G联合体2023-2024学年高二下学期期末考试数学试卷宁夏回族自治区石嘴山市第一中学2023-2024学年高二下学期期末考试数学试题(已下线)第11题 利用均值解决决策型问题(压轴题)
3 . 在“飞彩镌流年”文艺汇演中,诸位参赛者一展风采,奉上了一场舞与乐的盛宴.现从2000位参赛者中随机抽取40位幸运嘉宾,统计他们的年龄数据,得样本平均数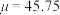 .
.
(1)若所有参赛者年龄 服从正态分布
服从正态分布 ,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
(2)若该文艺汇演对所有参赛者的表演作品进行评级,每位参赛者只有一个表演作品且每位参赛者作品有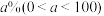 的概率评为
的概率评为 类,
类,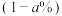 的概率评为
的概率评为 类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份
类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份 类作品的概率为
类作品的概率为 ,求
,求 的极大值点
的极大值点 ;
;
(3)以(2)中确定的 作为
作为 的值,记上述幸运嘉宾的作品中的
的值,记上述幸运嘉宾的作品中的 类作品数为
类作品数为 ,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲:
,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲: 类作品参赛者获得1000元现金,
类作品参赛者获得1000元现金, 类作品参赛者获得100元现金;乙:
类作品参赛者获得100元现金;乙: 类作品参赛者获得3000元现金,
类作品参赛者获得3000元现金, 类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
附:若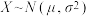 ,则
,则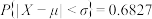 ,
,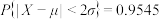 ,
,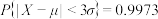 .
.
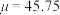 .
.(1)若所有参赛者年龄
 服从正态分布
服从正态分布 ,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);
,请估计参赛者年龄在30岁以上的人数(计算结果四舍五入取整数);(2)若该文艺汇演对所有参赛者的表演作品进行评级,每位参赛者只有一个表演作品且每位参赛者作品有
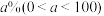 的概率评为
的概率评为 类,
类,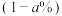 的概率评为
的概率评为 类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份
类,每位参赛者作品的评级结果相互独立.记上述40位幸运嘉宾的作品中恰有2份 类作品的概率为
类作品的概率为 ,求
,求 的极大值点
的极大值点 ;
;(3)以(2)中确定的
 作为
作为 的值,记上述幸运嘉宾的作品中的
的值,记上述幸运嘉宾的作品中的 类作品数为
类作品数为 ,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲:
,若对这些幸运嘉宾进行颁奖,现有两种颁奖方式:甲: 类作品参赛者获得1000元现金,
类作品参赛者获得1000元现金, 类作品参赛者获得100元现金;乙:
类作品参赛者获得100元现金;乙: 类作品参赛者获得3000元现金,
类作品参赛者获得3000元现金, 类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.
类作品参赛者不获得现金奖励.根据奖金期望判断主办方选择何种颁奖方式,成本可能更低.附:若
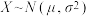 ,则
,则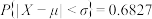 ,
,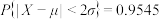 ,
,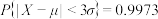 .
.
您最近一年使用:0次
4 . 某商场举行有奖促销活动,凡5月1日当天消费不低于1000元,均可抽奖一次,抽奖箱里有6个形状、大小、质地完全相同的小球,其中红球有4个,白球有2个,抽奖方案设置两种,顾客自行选择其中的一种方案.
方案一:从抽奖箱中,一次性摸出3个球,每有1个红球,可立减80元;
方案二:从抽奖箱中,有放回地每次摸出1个球,连摸3次,每摸到1次红球,立减80元.
(1)设方案一摸出的红球个数为随机变量X,求X的分布列、数学期望和方差;
(2)设方案二摸出的红球个数为随机变量Y,求Y的分布列、数学期望和方差;
(3)如果你是顾客,如何在上述两种抽奖方式中进行选择?请写出你的选择及简要理由.
方案一:从抽奖箱中,一次性摸出3个球,每有1个红球,可立减80元;
方案二:从抽奖箱中,有放回地每次摸出1个球,连摸3次,每摸到1次红球,立减80元.
(1)设方案一摸出的红球个数为随机变量X,求X的分布列、数学期望和方差;
(2)设方案二摸出的红球个数为随机变量Y,求Y的分布列、数学期望和方差;
(3)如果你是顾客,如何在上述两种抽奖方式中进行选择?请写出你的选择及简要理由.
您最近一年使用:0次
名校
5 . 某商场在开业当天进行有奖促销活动,规定该商场购物金额前100名的顾客,均可获得3次抽奖机会.每次中奖的概率为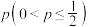 ,每次中奖与否相互不影响.中奖1次可获得100元奖金,中奖2次可获得300元奖金,中奖3次可获得500元奖金.
,每次中奖与否相互不影响.中奖1次可获得100元奖金,中奖2次可获得300元奖金,中奖3次可获得500元奖金.
(1)已知 ,求顾客甲获得了300元奖金的条件下,甲第一次抽奖就中奖的概率;
,求顾客甲获得了300元奖金的条件下,甲第一次抽奖就中奖的概率;
(2)已知该商场开业促销活动的经费为2万元,问该活动是否会超过预算?请说明理由.
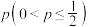 ,每次中奖与否相互不影响.中奖1次可获得100元奖金,中奖2次可获得300元奖金,中奖3次可获得500元奖金.
,每次中奖与否相互不影响.中奖1次可获得100元奖金,中奖2次可获得300元奖金,中奖3次可获得500元奖金.(1)已知
 ,求顾客甲获得了300元奖金的条件下,甲第一次抽奖就中奖的概率;
,求顾客甲获得了300元奖金的条件下,甲第一次抽奖就中奖的概率;(2)已知该商场开业促销活动的经费为2万元,问该活动是否会超过预算?请说明理由.
您最近一年使用:0次
名校
6 . 2023年五一劳动节前夕,某公司为全体员工发放奖励,奖励拟采用抽签方式发放:每位员工分别从标有不同面值的4张卡片中随机取出2张,2张卡片上的面值之和即为该员工的奖励金额.
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
您最近一年使用:0次
解题方法
7 . 某省高考自2024年起数学考试多选题(题号9~11)的计分标准是:每道题满分6分,全部选对得6分,部分选对得部分分(若某道题正确选项为两个,漏选一个正确选项得3分;若某道题正确选项为三个,漏选一个正确选项得4分,漏选两个正确选项得2分),错选或不选得0分.每道多选题共4个选项,正确答案是选两项或选三项.统计规律显示:多选题正确答案是“选两项”的概率是 ,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
(1)假设甲同学第10题随机选了两个选项,第11题随机选了一个选项,求甲同学这三道多选题(满分18分)所有可能总得分的中位数;
(2)假设第10题正确答案是“选两项”,若乙同学不知道是“选两项”,随机选该题的选项(既没空选也没选四项,所有选法等可能),求乙第10题得0分的概率 ;
;
(3)第11题甲同学采用“随机猜一个选项”的答题策略,乙同学采用“随机猜两个选项”的答题策略,记甲同学该题的得分为X,乙同学该题的得分为Y,试比较两同学得分的平均值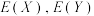 的大小.
的大小.
 ,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.
,没有同学选四项.甲、乙两个同学参加了考前模拟测试,已知两同学第9题选的全对,第10~11题还不确定对错.(1)假设甲同学第10题随机选了两个选项,第11题随机选了一个选项,求甲同学这三道多选题(满分18分)所有可能总得分的中位数;
(2)假设第10题正确答案是“选两项”,若乙同学不知道是“选两项”,随机选该题的选项(既没空选也没选四项,所有选法等可能),求乙第10题得0分的概率
 ;
;(3)第11题甲同学采用“随机猜一个选项”的答题策略,乙同学采用“随机猜两个选项”的答题策略,记甲同学该题的得分为X,乙同学该题的得分为Y,试比较两同学得分的平均值
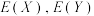 的大小.
的大小.
您最近一年使用:0次
名校
8 . 节日在即,某店家为此购入一批袋装糖果(每袋 ),现从中随机抽取100袋,将它们进行分级,统计结果如下:
),现从中随机抽取100袋,将它们进行分级,统计结果如下:
(1)若将频率视为概率,从这100袋糖果中有放回地随机抽取4袋,求恰好有2袋是三等品的概率;
(2)用样本估计总体,该店家制定了两种销售方案:
方案一:将糖果混合后不分类售出,售价为20元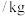 ;
;
方案二:按品级出售,售价如下:
为追求更高利润,该店家应采用哪种方案?
(3)用分层抽样的方法从这100袋糖果中抽取10袋,再从抽取的10袋糖果中随机抽取3袋,记抽到一等品的袋数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
 ),现从中随机抽取100袋,将它们进行分级,统计结果如下:
),现从中随机抽取100袋,将它们进行分级,统计结果如下:| 等级 | 一等品 | 二等品 | 三等品 |
| 袋数 | 40 | 40 | 20 |
(2)用样本估计总体,该店家制定了两种销售方案:
方案一:将糖果混合后不分类售出,售价为20元
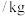 ;
;方案二:按品级出售,售价如下:
| 等级 | 一等品 | 二等品 | 三等品 |
售价(元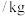 ) ) | 24 | 22 | 17 |
(3)用分层抽样的方法从这100袋糖果中抽取10袋,再从抽取的10袋糖果中随机抽取3袋,记抽到一等品的袋数为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
名校
9 . 某商场回馈消费者,举办活动,规则如下:每5位消费者组成一组,每人从 三个字母中随机抽取一个,抽取相同字母最少的人每人获得300元奖励.(例如:5人中2人选
三个字母中随机抽取一个,抽取相同字母最少的人每人获得300元奖励.(例如:5人中2人选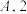 人选
人选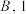 人选
人选 ,则选择
,则选择 的人获奖;5人中3人选
的人获奖;5人中3人选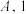 人选
人选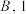 人选
人选 ,则选择
,则选择 和
和 的人均获奖;如
的人均获奖;如 中有一个或两个字母没人选择,则无人获奖)
中有一个或两个字母没人选择,则无人获奖)
(1)若甲和乙在同一组,求甲获奖的前提下,乙获奖的概率;
(2)设每组5人中获奖人数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)商家提供方案2:将 三个字母改为
三个字母改为 和
和 两个字母,其余规则不变,获奖的每个人奖励200元.作为消费者,站在每组5人获取总奖金的数学期望的角度分析,你是否选择方案2?
两个字母,其余规则不变,获奖的每个人奖励200元.作为消费者,站在每组5人获取总奖金的数学期望的角度分析,你是否选择方案2?
 三个字母中随机抽取一个,抽取相同字母最少的人每人获得300元奖励.(例如:5人中2人选
三个字母中随机抽取一个,抽取相同字母最少的人每人获得300元奖励.(例如:5人中2人选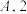 人选
人选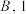 人选
人选 ,则选择
,则选择 的人获奖;5人中3人选
的人获奖;5人中3人选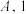 人选
人选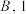 人选
人选 ,则选择
,则选择 和
和 的人均获奖;如
的人均获奖;如 中有一个或两个字母没人选择,则无人获奖)
中有一个或两个字母没人选择,则无人获奖)(1)若甲和乙在同一组,求甲获奖的前提下,乙获奖的概率;
(2)设每组5人中获奖人数为随机变量
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(3)商家提供方案2:将
 三个字母改为
三个字母改为 和
和 两个字母,其余规则不变,获奖的每个人奖励200元.作为消费者,站在每组5人获取总奖金的数学期望的角度分析,你是否选择方案2?
两个字母,其余规则不变,获奖的每个人奖励200元.作为消费者,站在每组5人获取总奖金的数学期望的角度分析,你是否选择方案2?
您最近一年使用:0次
名校
10 . 在我校开展的文化节知识竞赛活动中,共有A、B、C三道必答题,答对A、B、C分别得10分,10分,20分,答错不得分.已知甲同学答对问题A、B、C的概率分别为 ,
, ,
, ,乙同学答对问题A、B、C的概率均为
,乙同学答对问题A、B、C的概率均为 ,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
(1)求甲同学至少有一道题不能答对的概率;
(2)运用你学过的统计学知识判断,谁的得分能力更强.
 ,
, ,
, ,乙同学答对问题A、B、C的概率均为
,乙同学答对问题A、B、C的概率均为 ,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.(1)求甲同学至少有一道题不能答对的概率;
(2)运用你学过的统计学知识判断,谁的得分能力更强.
您最近一年使用:0次



