1 . 记集合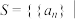 无穷数列
无穷数列 中存在有限项不为零,
中存在有限项不为零,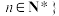 ,对任意
,对任意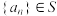 ,设变换
,设变换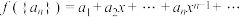 ,
,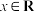 .定义运算
.定义运算 :若
:若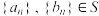 ,则
,则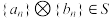 ,
,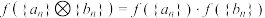 .
.
(1)若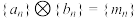 ,用
,用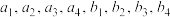 表示
表示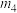 ;
;
(2)证明: ;
;
(3)若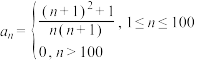 ,
,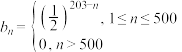 ,
,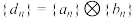 ,证明:
,证明: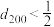 .
.
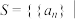 无穷数列
无穷数列 中存在有限项不为零,
中存在有限项不为零,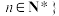 ,对任意
,对任意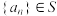 ,设变换
,设变换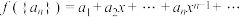 ,
,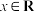 .定义运算
.定义运算 :若
:若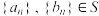 ,则
,则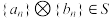 ,
,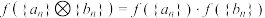 .
.(1)若
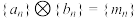 ,用
,用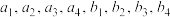 表示
表示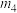 ;
;(2)证明:
 ;
;(3)若
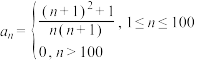 ,
,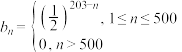 ,
,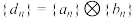 ,证明:
,证明: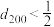 .
.
您最近一年使用:0次
2024-03-15更新
|
1834次组卷
|
4卷引用:拔高点突破01 新情景、新定义下的数列问题(七大题型)
(已下线)拔高点突破01 新情景、新定义下的数列问题(七大题型)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(过关集训)山东省青岛市2024届高三下学期第一次适应性检测数学试题广东省广州市广雅中学2024届高三下学期教学情况检测(一)数学试题
名校
解题方法
2 . 已知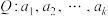 为有穷正整数数列,且
为有穷正整数数列,且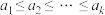 ,集合
,集合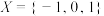 .若存在
.若存在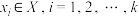 ,使得
,使得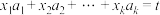 ,则称
,则称 为
为 可表数,称集合
可表数,称集合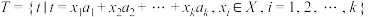 为
为 可表集.
可表集.
(1)若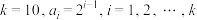 ,判定31,1024是否为
,判定31,1024是否为 可表数,并说明理由;
可表数,并说明理由;
(2)若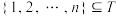 ,证明:
,证明: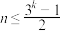 ;
;
(3)设 ,若
,若 ,求
,求 的最小值.
的最小值.
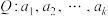 为有穷正整数数列,且
为有穷正整数数列,且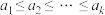 ,集合
,集合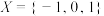 .若存在
.若存在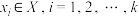 ,使得
,使得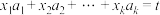 ,则称
,则称 为
为 可表数,称集合
可表数,称集合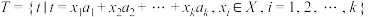 为
为 可表集.
可表集.(1)若
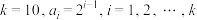 ,判定31,1024是否为
,判定31,1024是否为 可表数,并说明理由;
可表数,并说明理由;(2)若
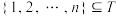 ,证明:
,证明: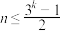 ;
;(3)设
 ,若
,若 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-01-20更新
|
2110次组卷
|
8卷引用:专题1 集合新定义题(九省联考第19题模式)练
(已下线)专题1 集合新定义题(九省联考第19题模式)练(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)北京市昌平区2024届高三上学期期末质量抽测数学试题江西省南昌市第二中学2024届高三“九省联考”考后适应性测试数学试题(三)北京市海淀区北京一零一中2023-2024学年高三下学期统考四(开学考)数学试题广东省梅州市大埔县虎山中学2023-2024学年高二下学期开学质量检测数学试卷河南省信阳市新县高级中学2024届高三考前第五次适应性考试数学试题广东省广州市广雅中学2024届高三下学期教学情况检测(二)数学试题
名校
3 . 已知: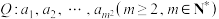 为有穷正整数数列,其最大项的值为
为有穷正整数数列,其最大项的值为 ,且当
,且当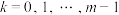 时,均有
时,均有 .设
.设 ,对于
,对于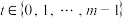 ,定义
,定义 ,其中,
,其中,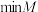 表示数集M中最小的数.
表示数集M中最小的数.
(1)若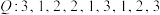 ,写出
,写出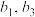 的值;
的值;
(2)若存在 满足:
满足: ,求
,求 的最小值;
的最小值;
(3)当 时,证明:对所有
时,证明:对所有 .
.
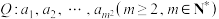 为有穷正整数数列,其最大项的值为
为有穷正整数数列,其最大项的值为 ,且当
,且当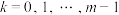 时,均有
时,均有 .设
.设 ,对于
,对于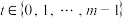 ,定义
,定义 ,其中,
,其中,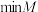 表示数集M中最小的数.
表示数集M中最小的数.(1)若
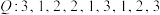 ,写出
,写出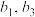 的值;
的值;(2)若存在
 满足:
满足: ,求
,求 的最小值;
的最小值;(3)当
 时,证明:对所有
时,证明:对所有 .
.
您最近一年使用:0次
2024-04-09更新
|
1635次组卷
|
4卷引用:2024年北京高考数学真题平行卷(提升)
(已下线)2024年北京高考数学真题平行卷(提升)北京市海淀区2024届高三下学期期中练习(一模)数学试题2024届河北省雄安新区部分高中高考三模数学试题甘肃省白银市靖远县第一中学2024届高三下学期模拟预测数学试题
名校
4 . 对于数列 ,如果存在正整数
,如果存在正整数 ,使得对任意
,使得对任意 ,都有
,都有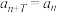 ,那么数列
,那么数列 就叫做周期数列,
就叫做周期数列, 叫做这个数列的周期.若周期数列
叫做这个数列的周期.若周期数列 满足:存在正整数
满足:存在正整数 ,对每一个
,对每一个 ,都有
,都有 ,我们称数列
,我们称数列 和
和 为“同根数列”.
为“同根数列”.
(1)判断数列 是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;
是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;
(2)若 和
和 是“同根数列”,且周期的最小值分别是
是“同根数列”,且周期的最小值分别是 和
和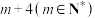 ,求
,求 的最大值.
的最大值.
 ,如果存在正整数
,如果存在正整数 ,使得对任意
,使得对任意 ,都有
,都有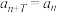 ,那么数列
,那么数列 就叫做周期数列,
就叫做周期数列, 叫做这个数列的周期.若周期数列
叫做这个数列的周期.若周期数列 满足:存在正整数
满足:存在正整数 ,对每一个
,对每一个 ,都有
,都有 ,我们称数列
,我们称数列 和
和 为“同根数列”.
为“同根数列”.(1)判断数列
 是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;
是否为周期数列.如果是,写出该数列的周期,如果不是,说明理由;(2)若
 和
和 是“同根数列”,且周期的最小值分别是
是“同根数列”,且周期的最小值分别是 和
和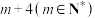 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
5 . 设 为整数.有穷数列
为整数.有穷数列 的各项均为正整数,其项数为m(
的各项均为正整数,其项数为m( ).若
).若 满足如下两个性质,则称
满足如下两个性质,则称 为
为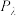 数列:①
数列:①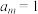 ,且
,且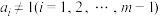 ;②
;②
(1)若 为
为 数列,且
数列,且 ,求m;
,求m;
(2)若 为
为 数列,求
数列,求 的所有可能值;
的所有可能值;
(3)若对任意的 数列
数列 ,均有
,均有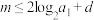 ,求d的最小值.
,求d的最小值.
 为整数.有穷数列
为整数.有穷数列 的各项均为正整数,其项数为m(
的各项均为正整数,其项数为m( ).若
).若 满足如下两个性质,则称
满足如下两个性质,则称 为
为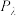 数列:①
数列:①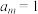 ,且
,且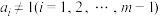 ;②
;②
(1)若
 为
为 数列,且
数列,且 ,求m;
,求m;(2)若
 为
为 数列,求
数列,求 的所有可能值;
的所有可能值;(3)若对任意的
 数列
数列 ,均有
,均有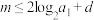 ,求d的最小值.
,求d的最小值.
您最近一年使用:0次
2023-05-05更新
|
2124次组卷
|
6卷引用:北京卷专题18数列(解答题)
北京卷专题18数列(解答题)(已下线)专题15 数列不等式的证明 微点1 反证法证明数列不等式(已下线)专题05 数列在高中数学其他模块的应用(九大题型+过关检测专训)-2023-2024学年高二数学《重难点题型·高分突破》(人教A版2019选择性必修第二册)北京市海淀区2023届高三二模数学试题北京市朝阳区2024届高三上学期数学期中模拟数学试题江苏省南京市南京外国语学校2024届高三下学期2月开学期初考试数学试题
6 . 若存在常数 ,使得数列
,使得数列 满足
满足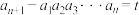 (
( ,
, ),则称数列
),则称数列 为“
为“ 数列”.
数列”.
(1)判断数列:1,2,3,8,49是否为“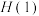 数列”,并说明理由;
数列”,并说明理由;
(2)若数列 是首项为
是首项为 的“
的“ 数列”,数列
数列”,数列 是等比数列,且
是等比数列,且 与
与 满足
满足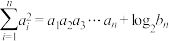 ,求
,求 的值和数列
的值和数列 的通项公式;
的通项公式;
(3)若数列 是“
是“ 数列”,
数列”, 为数列
为数列 的前
的前 项和,
项和, ,
, ,试比较
,试比较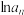 与
与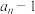 的大小,并证明
的大小,并证明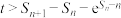 .
.
 ,使得数列
,使得数列 满足
满足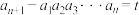 (
( ,
, ),则称数列
),则称数列 为“
为“ 数列”.
数列”.(1)判断数列:1,2,3,8,49是否为“
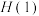 数列”,并说明理由;
数列”,并说明理由;(2)若数列
 是首项为
是首项为 的“
的“ 数列”,数列
数列”,数列 是等比数列,且
是等比数列,且 与
与 满足
满足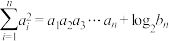 ,求
,求 的值和数列
的值和数列 的通项公式;
的通项公式;(3)若数列
 是“
是“ 数列”,
数列”, 为数列
为数列 的前
的前 项和,
项和, ,
, ,试比较
,试比较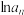 与
与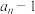 的大小,并证明
的大小,并证明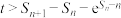 .
.
您最近一年使用:0次
2023-12-14更新
|
1657次组卷
|
12卷引用:2024年高考数学全真模拟卷05(新题型地区专用)
(已下线)2024年高考数学全真模拟卷05(新题型地区专用)(已下线)黄金卷05(已下线)新高考预测卷(2024新试卷结构)(已下线)微考点4-1 新高考新试卷结构压轴题新定义数列试题分类汇编(已下线)专题05 数列(四大类型题)15区新题速递(已下线)专题09 导数(三大类型题)15区新题速递(已下线)湖南省长沙市四县区2024届高三下学期3月调研考试数学试题变式题16-19上海市普陀区2024届高考一模数学试题2024届高三新改革数学模拟预测训练二(九省联考题型)湖南省长沙市四县区2024届高三下学期3月调研考试数学试卷江西省五市九校协作体2024届高三下学期第二次联考数学试卷江西省赣州市文清外国语学校2025届高三上学期开学考试数学试卷
22-23高三下·北京海淀·开学考试
名校
解题方法
7 . 若无穷数列 的各项均为整数.且对于
的各项均为整数.且对于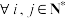 ,
, ,都存在
,都存在 ,使得
,使得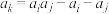 ,则称数列
,则称数列 满足性质P.
满足性质P.
(1)判断下列数列是否满足性质P,并说明理由.
① ,
, ,2,3,…;
,2,3,…;
②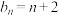 ,
, ,2,3,….
,2,3,….
(2)若数列 满足性质P,且
满足性质P,且 ,求证:集合
,求证:集合 为无限集;
为无限集;
(3)若周期数列 满足性质P,求数列
满足性质P,求数列 的通项公式.
的通项公式.
 的各项均为整数.且对于
的各项均为整数.且对于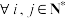 ,
, ,都存在
,都存在 ,使得
,使得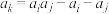 ,则称数列
,则称数列 满足性质P.
满足性质P.(1)判断下列数列是否满足性质P,并说明理由.
①
 ,
, ,2,3,…;
,2,3,…;②
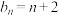 ,
, ,2,3,….
,2,3,….(2)若数列
 满足性质P,且
满足性质P,且 ,求证:集合
,求证:集合 为无限集;
为无限集;(3)若周期数列
 满足性质P,求数列
满足性质P,求数列 的通项公式.
的通项公式.
您最近一年使用:0次
2024-02-10更新
|
2084次组卷
|
14卷引用:2023年北京高考数学真题变式题16-21
(已下线)2023年北京高考数学真题变式题16-21(已下线)压轴题05数列压轴题15题型汇总-1(已下线)北京市海淀区清华大学附属中学2023届高三下学期开学调研测试数学试题北京市第五中学2023届高三下学期3月检测数学试题北京市海淀区教师进修学校附属实验学校2023届高三零模数学试题北京市海淀区中国人民大学附属中学2022-2023学年高二下学期期中数学复习试题(2)北京市海淀区首都师范大学附属中学2023-2024学年高三上学期阶段练习(1月)数学试题北京市清华大学附属中学2023届高三下学期4月月考数学试题(已下线)北京市第四中学2023-2024学年高三下学期开学考试数学试题湖南省2024届高三数学新改革提高训练一(九省联考题型)2024届高三新改革数学模拟预测训练一(九省联考题型)湖南省张家界市民族中学2023-2024学年高二下学期入学考试数学试题北京市顺义区第一中学2024届高三下学期高考考前适应性检测数学试卷广东省广州市执信中学2024届高三下学期教学情况检测(二)数学试题
名校
8 . 若有穷自然数数列 :
: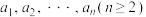 满足如下两个性质,则称
满足如下两个性质,则称 为
为 数列:
数列:
① ,其中,
,其中,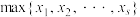 表示
表示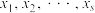 ,这
,这 个数中最大的数;
个数中最大的数;
② ,其中,
,其中,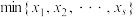 表示
表示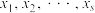 ,这
,这 个数中最小的数.
个数中最小的数.
(1)判断 :2,4,6,7,10是否为
:2,4,6,7,10是否为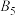 数列,说明理由;
数列,说明理由;
(2)若 :
: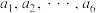 是
是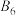 数列,且
数列,且 ,
, ,
, 成等比数列,求
成等比数列,求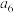 ;
;
(3)证明:对任意 数列
数列 :
: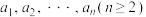 ,存在实数
,存在实数 ,使得
,使得 .(
.( 表示不超过
表示不超过 的最大整数)
的最大整数)
 :
: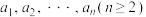 满足如下两个性质,则称
满足如下两个性质,则称 为
为 数列:
数列:①
 ,其中,
,其中,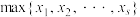 表示
表示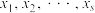 ,这
,这 个数中最大的数;
个数中最大的数;②
 ,其中,
,其中,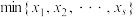 表示
表示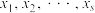 ,这
,这 个数中最小的数.
个数中最小的数.(1)判断
 :2,4,6,7,10是否为
:2,4,6,7,10是否为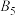 数列,说明理由;
数列,说明理由;(2)若
 :
: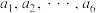 是
是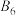 数列,且
数列,且 ,
, ,
, 成等比数列,求
成等比数列,求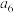 ;
;(3)证明:对任意
 数列
数列 :
: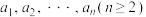 ,存在实数
,存在实数 ,使得
,使得 .(
.( 表示不超过
表示不超过 的最大整数)
的最大整数)
您最近一年使用:0次
2024-04-09更新
|
1481次组卷
|
4卷引用:2024年北京高考数学真题变式题16-21
(已下线)2024年北京高考数学真题变式题16-21(已下线)拔高点突破01 新情景、新定义下的数列问题(七大题型)北京市朝阳区2024届高三下学期质量检测一数学试题北京市大峪中学2025届高三上学期开学定位考试数学试题
9 . 设集合 是一个非空数集,对任意
是一个非空数集,对任意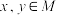 ,定义
,定义 ,称
,称 为集合
为集合 的一个度量,称集合
的一个度量,称集合 为一个对于度量
为一个对于度量 而言的度量空间,该度量空间记为
而言的度量空间,该度量空间记为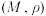 .
.
定义1:若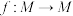 是度量空间
是度量空间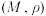 上的一个函数,且存在
上的一个函数,且存在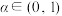 ,使得对任意
,使得对任意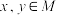 ,均有:
,均有: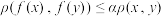 ,则称
,则称 是度量空间
是度量空间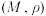 上的一个“压缩函数”.
上的一个“压缩函数”.
定义2:记无穷数列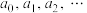 为
为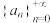 ,若
,若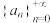 是度量空间
是度量空间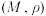 上的数列,且对任意正实数
上的数列,且对任意正实数 ,都存在一个正整数
,都存在一个正整数 ,使得对任意正整数
,使得对任意正整数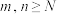 ,均有
,均有 ,则称
,则称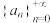 是度量空间
是度量空间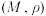 上的一个“基本数列”.
上的一个“基本数列”.
(1)设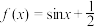 ,证明:
,证明: 是度量空间
是度量空间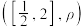 上的一个“压缩函数”;
上的一个“压缩函数”;
(2)已知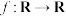 是度量空间
是度量空间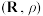 上的一个压缩函数,且
上的一个压缩函数,且 ,定义
,定义 ,
, ,证明:
,证明: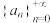 为度量空间
为度量空间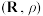 上的一个“基本数列”.
上的一个“基本数列”.
 是一个非空数集,对任意
是一个非空数集,对任意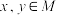 ,定义
,定义 ,称
,称 为集合
为集合 的一个度量,称集合
的一个度量,称集合 为一个对于度量
为一个对于度量 而言的度量空间,该度量空间记为
而言的度量空间,该度量空间记为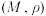 .
.定义1:若
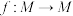 是度量空间
是度量空间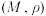 上的一个函数,且存在
上的一个函数,且存在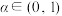 ,使得对任意
,使得对任意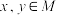 ,均有:
,均有: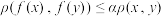 ,则称
,则称 是度量空间
是度量空间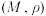 上的一个“压缩函数”.
上的一个“压缩函数”.定义2:记无穷数列
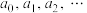 为
为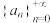 ,若
,若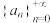 是度量空间
是度量空间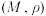 上的数列,且对任意正实数
上的数列,且对任意正实数 ,都存在一个正整数
,都存在一个正整数 ,使得对任意正整数
,使得对任意正整数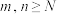 ,均有
,均有 ,则称
,则称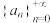 是度量空间
是度量空间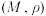 上的一个“基本数列”.
上的一个“基本数列”.(1)设
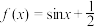 ,证明:
,证明: 是度量空间
是度量空间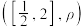 上的一个“压缩函数”;
上的一个“压缩函数”;(2)已知
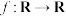 是度量空间
是度量空间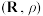 上的一个压缩函数,且
上的一个压缩函数,且 ,定义
,定义 ,
, ,证明:
,证明: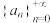 为度量空间
为度量空间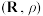 上的一个“基本数列”.
上的一个“基本数列”.
您最近一年使用:0次
2024-04-16更新
|
1386次组卷
|
4卷引用:压轴题01集合新定义、函数与导数13题型汇总-2
(已下线)压轴题01集合新定义、函数与导数13题型汇总-2河北省石家庄市2024届高三下学期教学质量检测(二)数学试卷湖北省恩施州巴东县2024届高三下学期教学质量检测(二)数学试题福建省龙岩市2024届高三适应性练习(三)数学试题
10 . 对于数列 ,称
,称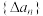 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .对正整数
.对正整数 ,称
,称 为数列
为数列 的
的 阶差分数列,其中
阶差分数列,其中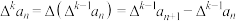 已知数列
已知数列 的首项
的首项 ,且
,且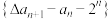 为
为 的二阶差分数列.
的二阶差分数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 为数列
为数列 的一阶差分数列,对
的一阶差分数列,对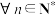 ,是否都有
,是否都有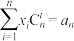 成立?并说明理由;(其中
成立?并说明理由;(其中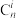 为组合数)
为组合数)
(3)对于(2)中的数列 ,令
,令 ,其中
,其中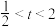 .证明:
.证明: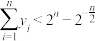 .
.
 ,称
,称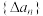 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .对正整数
.对正整数 ,称
,称 为数列
为数列 的
的 阶差分数列,其中
阶差分数列,其中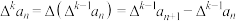 已知数列
已知数列 的首项
的首项 ,且
,且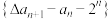 为
为 的二阶差分数列.
的二阶差分数列.(1)求数列
 的通项公式;
的通项公式;(2)设
 为数列
为数列 的一阶差分数列,对
的一阶差分数列,对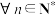 ,是否都有
,是否都有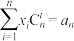 成立?并说明理由;(其中
成立?并说明理由;(其中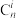 为组合数)
为组合数)(3)对于(2)中的数列
 ,令
,令 ,其中
,其中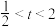 .证明:
.证明: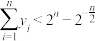 .
.
您最近一年使用:0次
2024-05-09更新
|
1371次组卷
|
7卷引用:拔高点突破01 新情景、新定义下的数列问题(七大题型)
(已下线)拔高点突破01 新情景、新定义下的数列问题(七大题型)(已下线)专题3 数列中的新定义压轴大题(过关集训)(已下线)第一章 排列组合与二项式定理 专题五 二项式定理 微点4 二项式定理综合训练【培优版】(已下线)第03讲 二项式定理(十五大题型)(练习)-2吉林省长春市东北师范大学附属中学2024届高三下学期第五次模拟考试数学试题甘肃省兰州市西北师大附中2024届高三第五次诊断考试(三模)数学试题福建省泉州市永春第一中学2024届高三最后一卷数学试卷



