1 . 初等数论中的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数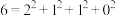 .设
.设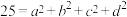 ,其中
,其中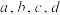 均为自然数,则满足条件的有序数组
均为自然数,则满足条件的有序数组 的个数是
的个数是__________ .(用数字作答)
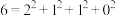 .设
.设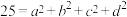 ,其中
,其中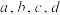 均为自然数,则满足条件的有序数组
均为自然数,则满足条件的有序数组 的个数是
的个数是
您最近一年使用:0次
2024-05-04更新
|
785次组卷
|
3卷引用:湖南师范大学附属中学2024届高三下学期模拟(二)数学试卷
解题方法
2 . 数学家Geminad Dandelin用一平面截圆锥后,在圆锥内放两个大小不同的小球,使得它们分别与圆锥侧面、截面相切,就可证明图中平面截圆锥得到的截面是椭圆(如图称为丹德林双球模型).若圆锥的轴截面为正三角形,则用与圆锥的轴成 角的平面截圆锥所得椭圆的离心率为
角的平面截圆锥所得椭圆的离心率为__________ .
 角的平面截圆锥所得椭圆的离心率为
角的平面截圆锥所得椭圆的离心率为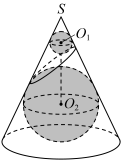
您最近一年使用:0次
名校
解题方法
3 . 假设视网膜为一个平面,光在空气中不折射,眼球的成像原理为小孔成像. 思考如下成像原理: 如图,地面内有圆 ,其圆心在线段
,其圆心在线段 上,且与线段
上,且与线段 交于不与
交于不与 重合的点
重合的点 ,
, 地面,且
地面,且 ,
, 点为人眼所在处,视网膜平面与直线
点为人眼所在处,视网膜平面与直线 垂直. 过
垂直. 过 点作平面
点作平面 平行于视网膜平面. 科学家已经证明,这种情况下圆
平行于视网膜平面. 科学家已经证明,这种情况下圆 上任意一点到
上任意一点到 点的直线与平面
点的直线与平面 交点的轨迹(令为曲线
交点的轨迹(令为曲线 )为椭圆或圆,且由于小孔成像,曲线
)为椭圆或圆,且由于小孔成像,曲线 与圆
与圆 在视网膜平面上的影像是相似的,则当视网膜平面上的圆
在视网膜平面上的影像是相似的,则当视网膜平面上的圆 的影像为圆时,圆
的影像为圆时,圆 的半径
的半径 为
为____________ . 当圆 的半径
的半径 满足
满足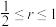 时,视网膜平面上的圆
时,视网膜平面上的圆 的影像的离心率的取值范围为
的影像的离心率的取值范围为____________ .
 ,其圆心在线段
,其圆心在线段 上,且与线段
上,且与线段 交于不与
交于不与 重合的点
重合的点 ,
, 地面,且
地面,且 ,
, 点为人眼所在处,视网膜平面与直线
点为人眼所在处,视网膜平面与直线 垂直. 过
垂直. 过 点作平面
点作平面 平行于视网膜平面. 科学家已经证明,这种情况下圆
平行于视网膜平面. 科学家已经证明,这种情况下圆 上任意一点到
上任意一点到 点的直线与平面
点的直线与平面 交点的轨迹(令为曲线
交点的轨迹(令为曲线 )为椭圆或圆,且由于小孔成像,曲线
)为椭圆或圆,且由于小孔成像,曲线 与圆
与圆 在视网膜平面上的影像是相似的,则当视网膜平面上的圆
在视网膜平面上的影像是相似的,则当视网膜平面上的圆 的影像为圆时,圆
的影像为圆时,圆 的半径
的半径 为
为 的半径
的半径 满足
满足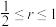 时,视网膜平面上的圆
时,视网膜平面上的圆 的影像的离心率的取值范围为
的影像的离心率的取值范围为
您最近一年使用:0次
2024-05-09更新
|
98次组卷
|
2卷引用:广东省广州市广东实验中学2024届高三教学情况测试(一)数学B卷
解题方法
4 . 用平面截圆锥面,可以截出椭圆、双曲线、抛物线,那它们是不是符合圆锥曲线的定义呢?比利时数学家旦德林用一个双球模型给出了证明.如图1,在一个圆锥中放入两个球,使得它们都与圆锥面相切,一个平面过圆锥母线上的点 且与两个球都相切,切点分别记为
且与两个球都相切,切点分别记为 .这个平面截圆锥面得到交线
.这个平面截圆锥面得到交线 是
是 上任意一点,过点
上任意一点,过点 的母线与两个球分别相切于点
的母线与两个球分别相切于点 ,因此有
,因此有 ,而
,而 是图中两个圆锥母线长的差,是一个定值,因此曲线
是图中两个圆锥母线长的差,是一个定值,因此曲线 是一个椭圆.如图2,两个对顶圆锥中,各有一个球,这两个球的半径相等且与圆锥面相切,已知这两个圆锥的母线与轴夹角的正切值为
是一个椭圆.如图2,两个对顶圆锥中,各有一个球,这两个球的半径相等且与圆锥面相切,已知这两个圆锥的母线与轴夹角的正切值为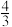 ,球的半径为4,平面
,球的半径为4,平面 与圆锥的轴平行,且与这两个球相切于
与圆锥的轴平行,且与这两个球相切于 两点,记平面
两点,记平面 与圆锥侧面相交所得曲线为
与圆锥侧面相交所得曲线为 ,则曲线
,则曲线 的离心率为
的离心率为__________ .
 且与两个球都相切,切点分别记为
且与两个球都相切,切点分别记为 .这个平面截圆锥面得到交线
.这个平面截圆锥面得到交线 是
是 上任意一点,过点
上任意一点,过点 的母线与两个球分别相切于点
的母线与两个球分别相切于点 ,因此有
,因此有 ,而
,而 是图中两个圆锥母线长的差,是一个定值,因此曲线
是图中两个圆锥母线长的差,是一个定值,因此曲线 是一个椭圆.如图2,两个对顶圆锥中,各有一个球,这两个球的半径相等且与圆锥面相切,已知这两个圆锥的母线与轴夹角的正切值为
是一个椭圆.如图2,两个对顶圆锥中,各有一个球,这两个球的半径相等且与圆锥面相切,已知这两个圆锥的母线与轴夹角的正切值为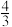 ,球的半径为4,平面
,球的半径为4,平面 与圆锥的轴平行,且与这两个球相切于
与圆锥的轴平行,且与这两个球相切于 两点,记平面
两点,记平面 与圆锥侧面相交所得曲线为
与圆锥侧面相交所得曲线为 ,则曲线
,则曲线 的离心率为
的离心率为
您最近一年使用:0次
解题方法
5 . 三等分角大约是在公元前五世纪由古希腊人提出来的,它和“立方倍积问题”“化圆为方问题”并称为“古代三大几何难题”.公元六世纪时,数学家帕普斯曾证明用一固定的双曲线可以解决“三等分角问题”.某同学在学习过程中,借用帕普斯的研究,使某锐角 的顶点与坐标原点
的顶点与坐标原点 重合,点
重合,点 在第四象限,且点
在第四象限,且点 在双曲线
在双曲线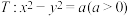 的一条渐近线上,而
的一条渐近线上,而 与
与 在第一象限内交于点
在第一象限内交于点 .以点
.以点 为圆心,
为圆心,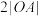 为半径的圆与
为半径的圆与 在第四象限内交于点
在第四象限内交于点 ,设
,设 的中点为
的中点为 ,则
,则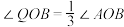 .若
.若 ,则
,则 的值为
的值为__________ .
 的顶点与坐标原点
的顶点与坐标原点 重合,点
重合,点 在第四象限,且点
在第四象限,且点 在双曲线
在双曲线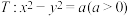 的一条渐近线上,而
的一条渐近线上,而 与
与 在第一象限内交于点
在第一象限内交于点 .以点
.以点 为圆心,
为圆心,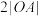 为半径的圆与
为半径的圆与 在第四象限内交于点
在第四象限内交于点 ,设
,设 的中点为
的中点为 ,则
,则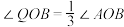 .若
.若 ,则
,则 的值为
的值为
您最近一年使用:0次
6 . 数论领域的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明.四平方和定理的内容是:任意正整数都可以表示为不超过四个自然数的平方和,例如正整数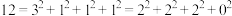 .设
.设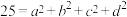 ,其中a,b,c,d均为自然数,则满足条件的有序数组
,其中a,b,c,d均为自然数,则满足条件的有序数组 的个数是
的个数是__________ .
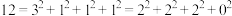 .设
.设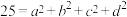 ,其中a,b,c,d均为自然数,则满足条件的有序数组
,其中a,b,c,d均为自然数,则满足条件的有序数组 的个数是
的个数是
您最近一年使用:0次
2023-04-05更新
|
2062次组卷
|
9卷引用:江苏省南京师范大学附属中学2022-2023学年高三一模适应性考试数学试题
江苏省南京师范大学附属中学2022-2023学年高三一模适应性考试数学试题辽宁省大连市康考迪亚高级中学2022-2023学年高三二模拟数学试题专题23计数原理与概率与统计(填空题)(已下线)第02讲 6.2.1排列+6.2.2排列数(3)(已下线)模块一专题1《排列与组合》单元检测篇B提升卷(已下线)模块五 专题6 全真拔高模拟6(已下线)6.2.1排列-6.2.2排列数——课堂例题(已下线)模块一 专题7《排列与组合》B提升卷(苏教版)云南省昆明市第八中学2023-2024学年高二下学期月考二数学试卷
名校
7 . 科拉茨是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数 ,如果
,如果 是偶数,就将它减半(即
是偶数,就将它减半(即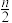 );如果
);如果 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即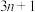 ),不断重复这样的运算,经过有限步后,一定可以得到1.这是一个很有趣的猜想,但目前还没有证明或否定.如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.这是一个很有趣的猜想,但目前还没有证明或否定.如果对正整数 (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则满足条件的
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则满足条件的 的所有不同值的和为
的所有不同值的和为___________ .
 ,如果
,如果 是偶数,就将它减半(即
是偶数,就将它减半(即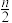 );如果
);如果 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即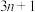 ),不断重复这样的运算,经过有限步后,一定可以得到1.这是一个很有趣的猜想,但目前还没有证明或否定.如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.这是一个很有趣的猜想,但目前还没有证明或否定.如果对正整数 (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则满足条件的
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则满足条件的 的所有不同值的和为
的所有不同值的和为
您最近一年使用:0次
2023-04-03更新
|
2292次组卷
|
6卷引用:湖南师范大学附属中学2023届高三一模数学试题
名校
解题方法
8 . 我们常常运用对同一个量算两次的方法来证明组合恒等式,如:从装有编号为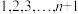 的
的 个球的口袋中取出
个球的口袋中取出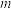 个球
个球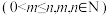 ,共有
,共有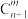 种取法.在
种取法.在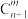 种取法中,不取
种取法中,不取 号球有
号球有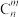 种取法;取
种取法;取 号球有
号球有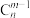 种取法.所以
种取法.所以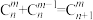 .试运用此方法,写出如下等式的结果:
.试运用此方法,写出如下等式的结果: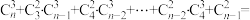
___________ .
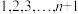 的
的 个球的口袋中取出
个球的口袋中取出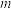 个球
个球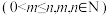 ,共有
,共有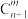 种取法.在
种取法.在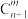 种取法中,不取
种取法中,不取 号球有
号球有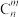 种取法;取
种取法;取 号球有
号球有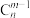 种取法.所以
种取法.所以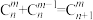 .试运用此方法,写出如下等式的结果:
.试运用此方法,写出如下等式的结果: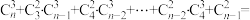
您最近一年使用:0次
2022-10-17更新
|
1614次组卷
|
9卷引用:辽宁省沈阳市东北育才学校2023届高三高考适应性测试(二)数学试题
辽宁省沈阳市东北育才学校2023届高三高考适应性测试(二)数学试题浙江省强基联盟2022-2023学年高二实验班上学期10月联考数学试题(已下线)专题20 计数原理(讲义)-1辽宁省丹东市五校2022-2023学年高三上学期联考数学试题(已下线)6.2.3-6.2.4 组合 组合数(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)7.3 组合(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)(已下线)专题18 排列组合与二项式定理江苏省常州市第一中学2023-2024学年高二上学期期末质量调研数学试题(已下线)专题01 两个计数原理与排列组合(7类压轴题型)-【常考压轴题】2023-2024学年高二数学压轴题攻略(人教A版2019选择性必修第三册)
名校
解题方法
9 . 如图是数学家Germinal Dandelin用来证明一个平面截圆锥得到的截口曲线是椭圆的模型.在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面与截面都相切,设图中球 ,球
,球 的半径分别为4和2,球心距离
的半径分别为4和2,球心距离 ,截面分别与球
,截面分别与球 ,球
,球 相切于点
相切于点 (
( 是截口椭圆的焦点),则此椭圆的离心率等于
是截口椭圆的焦点),则此椭圆的离心率等于__________ .
 ,球
,球 的半径分别为4和2,球心距离
的半径分别为4和2,球心距离 ,截面分别与球
,截面分别与球 ,球
,球 相切于点
相切于点 (
( 是截口椭圆的焦点),则此椭圆的离心率等于
是截口椭圆的焦点),则此椭圆的离心率等于
您最近一年使用:0次
2022-12-21更新
|
3609次组卷
|
15卷引用:广东省广州市2023届高三一模数学试题
广东省广州市2023届高三一模数学试题江苏省南通市海安高级中学2023届高三下学期一模数学试题广东省协和、华侨、增城中学2022-2023学年高二上学期期末数学试题(已下线)专题11 离心率问题速解(精讲精练)-3江苏省南通市海安高级中学2023届高三下学期3月阶段测试(四)数学试题(已下线)“8+4+4”小题强化训练(23)湖南省常德市临澧县第一中学2022-2023学年高二下学期5月第四阶段检测数学试题广东省广州市协和中学等三校2022-2023学年高二上学期期末联考数学试题福建省莆田第二中学、仙游第一中学2023-2024学年高二上学期期中联考数学试题广东省广州市三校(南实、铁一、广外)2023-2024学年高二上学期期中联考数学试题(已下线)期末真题必刷常考60题(32个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线) 第3章 圆锥曲线的方程单元测试能力卷-2023-2024学年高二数学上学期人教A版(2019)选择性必修第一册(已下线)高二数学第一学期期期末押题密卷02卷(已下线)专题7-2求曲线方程和动点轨迹归类-2江苏省无锡市锡东高级中学2024届高三下学期5月月考数学试题
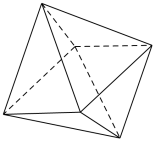
10 . 公元前6世纪,古希腊毕达哥拉斯学派已经知道五种正多面体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.后来,柏拉图学派的泰阿泰德证明出正多面体总共只有上述五种.如图所示的就是正八面体图形,从该正八面体的6个顶点中随机抽取2个,则这2个顶点的连线是该正八面体的一条棱的概率是______ .

您最近一年使用:0次
2022-06-07更新
|
105次组卷
|
4卷引用:河南省部分学校2022届高三下学期5月考前最后一卷文科数学试题



