名校
1 . 一个装有8个球的口袋中,有标号分别为1,2的2个红球和标号分别为1,2,3,4,5,6的6个蓝球,除颜色和标号外没有其他差异.从中任意摸1个球,设事件 “摸出的球是红球”,事件
“摸出的球是红球”,事件 “摸出的球标号为偶数”,事件
“摸出的球标号为偶数”,事件 “摸出的球标号为3的倍数”,则( )
“摸出的球标号为3的倍数”,则( )
 “摸出的球是红球”,事件
“摸出的球是红球”,事件 “摸出的球标号为偶数”,事件
“摸出的球标号为偶数”,事件 “摸出的球标号为3的倍数”,则( )
“摸出的球标号为3的倍数”,则( )| A.事件A与事件C互斥 |
| B.事件B与事件C互斥 |
| C.事件A与事件B相互独立 |
| D.事件B与事件C相互独立 |
您最近一年使用:0次
2023-02-07更新
|
1368次组卷
|
10卷引用:2022年浙江省宁波市高中数学竞赛试题
2022年浙江省宁波市高中数学竞赛试题(已下线)期末考测试(提升)一隅三反系列(人教A版2019必修第二册)山东省新泰市第一中学(老校区)2022-2023学年高一下学期第二次阶段性考试数学试题(已下线)专题13 概率综合(1)-期中期末考点大串讲安徽省六安第一中学2022-2023学年高一下学期期末考试数学试卷四川省宜宾市第四中学校2023-2024学年高二上学期期末数学试题四川省眉山市北外附属东坡外国语学校2023-2024学年高二下学期开学考试数学试题(已下线)第十章:概率(单元测试,新题型)--同步精品课堂(人教A版2019必修第二册)广东省佛山市第三中学2024-2025学年高二上学期第一次教学质量检测数学试卷广东省江门市新会华侨中学2024-2025学年高二上学期期中考试数学试题
名校
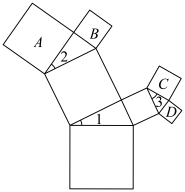
2 . 如图,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复上述操作(其中 ),得到四个小正方形
),得到四个小正方形 ,记它们的面积分别为
,记它们的面积分别为 ,则以下结论正确的是( )
,则以下结论正确的是( )
 ),得到四个小正方形
),得到四个小正方形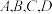 ,记它们的面积分别为
,记它们的面积分别为 ,则以下结论正确的是( )
,则以下结论正确的是( )
A. |
B. |
C.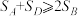 |
D.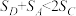 |
您最近一年使用:0次
2022-10-19更新
|
701次组卷
|
5卷引用:2022年全国中学生数学奥林匹克(预赛)贵州省初赛试题
22-23高三上·四川·阶段练习
名校
解题方法
3 . 如图,某菜农有一块等腰三角形菜地,其中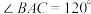 ,
,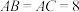 米.现将该三角形菜地分成三块,其中
米.现将该三角形菜地分成三块,其中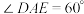 .
.

(1)若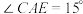 ,求
,求 的长;
的长;
(2)求 面积的最小值.
面积的最小值.
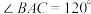 ,
,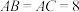 米.现将该三角形菜地分成三块,其中
米.现将该三角形菜地分成三块,其中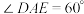 .
.
(1)若
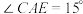 ,求
,求 的长;
的长;(2)求
 面积的最小值.
面积的最小值.
您最近一年使用:0次
2022-10-15更新
|
1043次组卷
|
7卷引用:河南省驻马店市确山县第一高级中学2022-2023学年高二上学期数学竞赛试题
名校
解题方法
4 . 设函数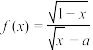 ,则下列说法正确的是( )
,则下列说法正确的是( )
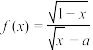 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若 ,则 ,则 在 在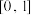 上单调递减 上单调递减 | B.若 , , 无最大值,也无最小值 无最大值,也无最小值 |
C.若 ,则 ,则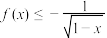 | D.若 ,则 ,则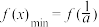 |
您最近一年使用:0次
2022-09-21更新
|
784次组卷
|
3卷引用:2022年浙江省温州市摇篮杯高一数学竞赛试题
名校
解题方法
5 . 近些年来,三维扫描技术得到空前发展,从而催生了数字几何这一新兴学科.数字几何是传统几何和计算机科学相结合的产物.数字几何中的一个重要概念是曲率,用曲率来刻画几何体的弯曲程度.规定:多面体在顶点处的曲率等于 与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有
与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有 个面角,每个面角是
个面角,每个面角是 ,所以正方体在各顶点的曲率为
,所以正方体在各顶点的曲率为  ,故其总曲率为
,故其总曲率为 .
.
(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率是常数.
.利用此定理试证明:简单多面体的总曲率是常数.
 与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有
与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有 个面角,每个面角是
个面角,每个面角是 ,所以正方体在各顶点的曲率为
,所以正方体在各顶点的曲率为  ,故其总曲率为
,故其总曲率为 .
.(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为
 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率是常数.
.利用此定理试证明:简单多面体的总曲率是常数.
您最近一年使用:0次
2022-09-19更新
|
1154次组卷
|
9卷引用:2022年浙江省温州市摇篮杯高一数学竞赛试题
2022年浙江省温州市摇篮杯高一数学竞赛试题(已下线)第01讲 空间几何体的结构、三视图和直观图与空间几何体的表面积和体积(练)(已下线)8.1 基本立体图形2(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)第五篇 向量与几何 专题21 曲率与曲率圆 微点3 曲率与曲率圆综合训练(已下线)11.2 锥体(第1课时)(七大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)(已下线)第八章立体几何8.1 空间几何体及其表面积与体积(已下线)专题14 棱柱、棱锥和棱台-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题6 以新定义为背景的相关问题【练】(高一期末压轴专项)(已下线)专题4 立体几何中的新定义压轴大题(过关集训)
名校
解题方法
6 . 现要将一边长为101的正方体 ,分割成两部分,要求如下:(1)分割截面交正方体各棱
,分割成两部分,要求如下:(1)分割截面交正方体各棱 ,
, ,
, ,
, 于点P,Q,R,S(可与顶点重合);(2)线段
于点P,Q,R,S(可与顶点重合);(2)线段 ,
, ,
, ,
,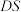 的长度均为非负整数,且线段
的长度均为非负整数,且线段 ,
, ,
, ,
,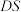 的每一组取值对应一种分割方式,则有
的每一组取值对应一种分割方式,则有___________ 种不同的分割方式.(用数字作答)
 ,分割成两部分,要求如下:(1)分割截面交正方体各棱
,分割成两部分,要求如下:(1)分割截面交正方体各棱 ,
, ,
, ,
, 于点P,Q,R,S(可与顶点重合);(2)线段
于点P,Q,R,S(可与顶点重合);(2)线段 ,
, ,
, ,
,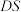 的长度均为非负整数,且线段
的长度均为非负整数,且线段 ,
, ,
, ,
,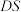 的每一组取值对应一种分割方式,则有
的每一组取值对应一种分割方式,则有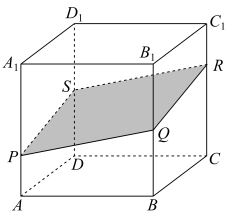
您最近一年使用:0次
2022-06-22更新
|
2268次组卷
|
3卷引用:2022年全国高中数学联赛江苏赛区苏州市选拔赛试题
名校
7 . 某旅游景区有如图所示A至H共8个停车位,现有2辆不同的白色车和2辆不同的黑色车,要求相同颜色的车不停在同一行也不停在同一列,则不同的停车方法总数为( )
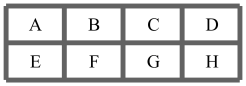
| A.288 | B.336 | C.576 | D.1680 |
您最近一年使用:0次
2022-05-25更新
|
3306次组卷
|
14卷引用:湖南省湘西州吉首市2022年第一届中小学生教师解题大赛数学试题
湖南省湘西州吉首市2022年第一届中小学生教师解题大赛数学试题湖北省武汉市2022届高三下学期五月模拟(二)数学试题江苏省泰州中学2022-2023学年高三上学期期初调研考试数学试题湖北省二十一所重点中学2023届高三上学期第二次联考数学试题(已下线)第01讲 分类加法计数原理与分步乘法计数原理 (精练)(已下线)8.1 计数原理及排列组合(精讲)湖南省长沙市第一中学2023届高三下学期月考(七)数学试题山东省菏泽市2022-2023学年高二下学期期末数学试题(已下线)2023年高三数学押题密卷四(已下线)6.1 分类加法计数原理与分步乘法计数原理(分层练习)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)广西百色市平果市铝城中学2024届高三下学期3月份测试数学试卷【人教A版(2019)】专题10计数原理(第二部分)-高二下学期名校期末好题汇编山东省枣庄市滕州市第一中学2023-2024学年高二下学期6月阶段性检测数学试题广东省肇庆市肇庆鼎湖中学2023-2024学年高二下学期期末统考模拟测试(6月月考)数学试题
名校
解题方法
8 . 如图,圆台上底面圆 半径为1,下底面圆
半径为1,下底面圆 半径为
半径为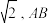 为圆台下底面的一条直径,圆
为圆台下底面的一条直径,圆 上点
上点 满足
满足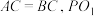 是圆台上底面的一条半径,点
是圆台上底面的一条半径,点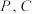 在平面
在平面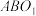 的同侧,且
的同侧,且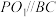 .
.

(1)证明:平面 平面
平面 ;
;
(2)若圆台的高为2,求直线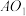 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 半径为1,下底面圆
半径为1,下底面圆 半径为
半径为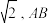 为圆台下底面的一条直径,圆
为圆台下底面的一条直径,圆 上点
上点 满足
满足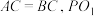 是圆台上底面的一条半径,点
是圆台上底面的一条半径,点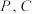 在平面
在平面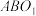 的同侧,且
的同侧,且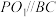 .
.
(1)证明:平面
 平面
平面 ;
;(2)若圆台的高为2,求直线
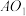 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-04-29更新
|
3065次组卷
|
9卷引用:湖南省湘西州吉首市2022年第一届中小学生教师解题大赛数学试题
9 . 现有下列三个条件:
①函数 的最小正周期为
的最小正周期为 ;
;
②函数 的图象可以由
的图象可以由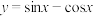 的图象平移得到;
的图象平移得到;
③函数 的图象相邻两条对称轴之间的距离
的图象相邻两条对称轴之间的距离 .
.
从中任选一个条件补充在下面的问题中,并作出正确解答.
已知向量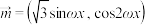 ,
,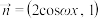 ,
, ,函数
,函数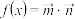 .且满足_________.
.且满足_________.
(1)求 的表达式,并求方程
的表达式,并求方程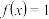 在闭区间
在闭区间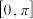 上的解;
上的解;
(2)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .已知
.已知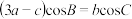 ,
, ,求
,求 的值.
的值.
①函数
 的最小正周期为
的最小正周期为 ;
;②函数
 的图象可以由
的图象可以由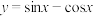 的图象平移得到;
的图象平移得到;③函数
 的图象相邻两条对称轴之间的距离
的图象相邻两条对称轴之间的距离 .
.从中任选一个条件补充在下面的问题中,并作出正确解答.
已知向量
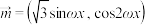 ,
,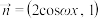 ,
, ,函数
,函数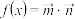 .且满足_________.
.且满足_________.(1)求
 的表达式,并求方程
的表达式,并求方程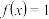 在闭区间
在闭区间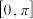 上的解;
上的解;(2)在
 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .已知
.已知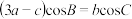 ,
, ,求
,求 的值.
的值.
您最近一年使用:0次
2021-09-08更新
|
1890次组卷
|
6卷引用:湖南省湘西州吉首市2022年第一届中小学生教师解题大赛数学试题



