解题方法
1 . “勾股数”,也被称为毕达哥拉斯树,是根据勾股定理所画出来的一个可以无限重复的树形图形.如图所示,以边长为4的正方形 的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若得到的“勾股树”上所存正方形的面积为96,则“勾股树”上所有正方形的个数为( )
的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若得到的“勾股树”上所存正方形的面积为96,则“勾股树”上所有正方形的个数为( )
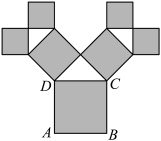
 的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若得到的“勾股树”上所存正方形的面积为96,则“勾股树”上所有正方形的个数为( )
的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若得到的“勾股树”上所存正方形的面积为96,则“勾股树”上所有正方形的个数为( )
| A.63 | B.64 | C.127 | D.128 |
您最近一年使用:0次
解题方法
2 . 希罗平均数(Heronianmean)是两个非负实数的一种平均,若 ,
, 是两个非负实数,则它们的希罗平均数
是两个非负实数,则它们的希罗平均数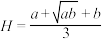 .记
.记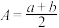 ,
,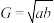 ,则
,则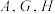 从小到大的关系为
从小到大的关系为______ .(用“≤”连接)
 ,
, 是两个非负实数,则它们的希罗平均数
是两个非负实数,则它们的希罗平均数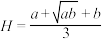 .记
.记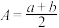 ,
,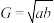 ,则
,则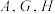 从小到大的关系为
从小到大的关系为
您最近一年使用:0次
2024-01-12更新
|
157次组卷
|
2卷引用:江苏省淮安市楚州中学2023-2024学年高一上学期12月教学质量调研数学试题
名校
3 . 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图1,点 ,
, ,
, 在水平线
在水平线 上,
上, 和
和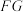 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,
是两个垂直于水平面且等高的测量标杆的高度,称为“表高”, 称为“表距”,
称为“表距”, 和
和 都称为“表目距”,
都称为“表目距”, 与
与 的差称为“表目距的差”,则海岛的高
的差称为“表目距的差”,则海岛的高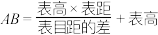 ,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线
,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线 上,同时在水平线
上,同时在水平线 上放一个小镜子(视为点
上放一个小镜子(视为点 ),他在距离镜子
),他在距离镜子 米点
米点 时,通过镜子看到了山顶,然后沿水平线
时,通过镜子看到了山顶,然后沿水平线 向靠近山的方向走了
向靠近山的方向走了 米,到达
米,到达 点,再将镜子放在距离自己
点,再将镜子放在距离自己 米的前方点
米的前方点 处,此时又看到了山顶,若此人的眼睛到水平线
处,此时又看到了山顶,若此人的眼睛到水平线 的距离为
的距离为 米,则此山的高度约为( )米
米,则此山的高度约为( )米

 ,
, ,
, 在水平线
在水平线 上,
上, 和
和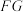 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,
是两个垂直于水平面且等高的测量标杆的高度,称为“表高”, 称为“表距”,
称为“表距”, 和
和 都称为“表目距”,
都称为“表目距”, 与
与 的差称为“表目距的差”,则海岛的高
的差称为“表目距的差”,则海岛的高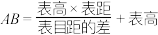 ,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线
,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线 上,同时在水平线
上,同时在水平线 上放一个小镜子(视为点
上放一个小镜子(视为点 ),他在距离镜子
),他在距离镜子 米点
米点 时,通过镜子看到了山顶,然后沿水平线
时,通过镜子看到了山顶,然后沿水平线 向靠近山的方向走了
向靠近山的方向走了 米,到达
米,到达 点,再将镜子放在距离自己
点,再将镜子放在距离自己 米的前方点
米的前方点 处,此时又看到了山顶,若此人的眼睛到水平线
处,此时又看到了山顶,若此人的眼睛到水平线 的距离为
的距离为 米,则此山的高度约为( )米
米,则此山的高度约为( )米
A.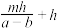 | B.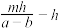 | C.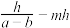 | D. |
您最近一年使用:0次
4 . 中国文化之美照亮生活,宋代的几何图案(图1)注重理性和逻辑的文化风气,中式美学的另一种浪漫,蕴含着数学对称之美.几何图案由函数,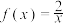 ,
, 与函数
与函数 (
( )图像(如图2)分别关于
)图像(如图2)分别关于 轴、
轴、 轴及原点
轴及原点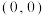 对称所得(如图3).
对称所得(如图3).

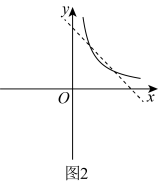
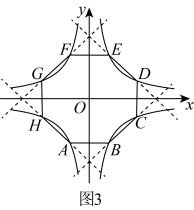
(1)若图3构成正八边形 ,求实数m的值;
,求实数m的值;
(2)若关于 的方程
的方程 有两个不相等实数根
有两个不相等实数根 ,
, .
.
①求实数m的取值范围;
②求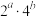 的最小值.
的最小值.
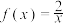 ,
, 与函数
与函数 (
( )图像(如图2)分别关于
)图像(如图2)分别关于 轴、
轴、 轴及原点
轴及原点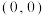 对称所得(如图3).
对称所得(如图3).


(1)若图3构成正八边形
 ,求实数m的值;
,求实数m的值;(2)若关于
 的方程
的方程 有两个不相等实数根
有两个不相等实数根 ,
, .
.①求实数m的取值范围;
②求
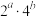 的最小值.
的最小值.
您最近一年使用:0次
5 . 杭州第19届亚运会的主会场——杭州奥体中心体育场,又称“大莲花”(如图1所示).会场造型取意于杭州丝绸纹理与纺织体系,建筑体态源于钱塘江水的动态,其简笔画如图2所示.一同学初学简笔画,先画了一个椭圆与圆弧的线稿,如图3所示.若椭圆 的方程为
的方程为 ,下顶点为
,下顶点为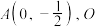 为坐标原点,
为坐标原点, 为圆
为圆 上任意一点,满足
上任意一点,满足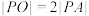 ,则点
,则点 的坐标为
的坐标为__________ ;若 为椭圆上一动点,当
为椭圆上一动点,当 取最大值时,点
取最大值时,点 恰好有两个,则
恰好有两个,则 的取值范围为
的取值范围为__________ .
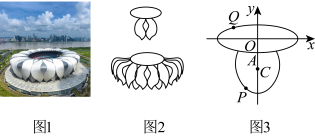
 的方程为
的方程为 ,下顶点为
,下顶点为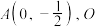 为坐标原点,
为坐标原点, 为圆
为圆 上任意一点,满足
上任意一点,满足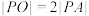 ,则点
,则点 的坐标为
的坐标为 为椭圆上一动点,当
为椭圆上一动点,当 取最大值时,点
取最大值时,点 恰好有两个,则
恰好有两个,则 的取值范围为
的取值范围为
您最近一年使用:0次
2023-11-09更新
|
225次组卷
|
2卷引用:江苏省淮安市2023-2024学年高二上学期11月期中数学试题
名校
解题方法
6 . 法国天文学家乔凡尼·多美尼科·卡西尼在研究土星及其卫星的运动规律时,发现了平面内到两个定点的距离之积为常数的点的轨迹,并称之为卡西尼卵形线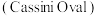 .在平面直角坐标系
.在平面直角坐标系 中,两个定点
中,两个定点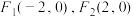 ,曲线
,曲线 是到两个定点
是到两个定点 的距离之积为
的距离之积为 的点的轨迹,以下结论正确的有( )
的点的轨迹,以下结论正确的有( )
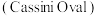 .在平面直角坐标系
.在平面直角坐标系 中,两个定点
中,两个定点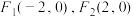 ,曲线
,曲线 是到两个定点
是到两个定点 的距离之积为
的距离之积为 的点的轨迹,以下结论正确的有( )
的点的轨迹,以下结论正确的有( )A.曲线 关于 关于 轴对称 轴对称 |
B.曲线 可能过坐标原点 可能过坐标原点 |
C. 为曲线 为曲线 上任意一点,当 上任意一点,当 时,点 时,点 纵坐标的取值范围为 纵坐标的取值范围为 |
D.若曲线 与椭圆 与椭圆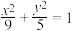 有公共点,则 有公共点,则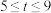 |
您最近一年使用:0次
2023-11-09更新
|
757次组卷
|
4卷引用:江苏省淮安市2023-2024学年高二上学期11月期中数学试题
江苏省淮安市2023-2024学年高二上学期11月期中数学试题江苏省淮安中学2023-2024学年高二上学期期中数学试题(已下线)专题5 曲线轨迹与交点问题(已下线)2024年新课标全国Ⅰ卷数学真题平行卷(提升)
7 . 谢尔宾斯基(Sierpinski)三角形是一种分形,它的构造方法如下:取一个实心等边三角形(如图1),沿三边中点的连线,将它分成四个小三角形,挖去中间小三角形(如图2),对剩下的三个小三角形继续以上操作(如图3),按照这样的方法得到的三角形就是谢尔宾斯基三角形.如果图1三角形的边长为2,则图4被挖去的三角形面积之和是( )
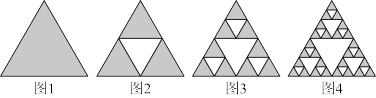
A.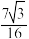 | B.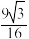 | C.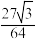 | D.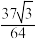 |
您最近一年使用:0次
2023-09-15更新
|
1156次组卷
|
6卷引用:江苏省淮安市2023-2024学年高三上学期第一次调研测试数学试题
江苏省淮安市2023-2024学年高三上学期第一次调研测试数学试题(已下线)第04讲 4.3.1等比数列的概念(6类热点题型讲练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第二册)吉林省延边州2024届高三下学期教学质量检测一模数学试题(已下线)4.3.1等比数列的概念(第2课时)(分层作业)(4种题型)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第二册)(已下线)黄金卷01(已下线)专题06 数列
8 . 《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至多有1个阴数的概率为( )
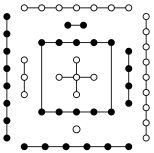
A. | B. | C. | D. |
您最近一年使用:0次
2023-08-13更新
|
788次组卷
|
7卷引用:江苏省淮安市涟水县第一中学2022-2023学年高二下学期5月月考数学试题
江苏省淮安市涟水县第一中学2022-2023学年高二下学期5月月考数学试题(已下线)6.4.2超几何分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)7.4.2超几何分布练习(已下线)专题20 概率与统计常考小题归类(15大题型)(练习)(已下线)7.4.2超几何分布(分层练习,4大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)7.4.2 超几何分布——课后作业(提升版)(已下线)7.4 二项分布与超几何分布(8大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
解题方法
9 . 我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“ ”和阴爻“
”和阴爻“ ”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有2个阳爻且2个阳爻不相邻的概率是( )
”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有2个阳爻且2个阳爻不相邻的概率是( )

A. | B.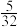 | C. | D. |
您最近一年使用:0次
解题方法
10 . 1626年,阿贝尔特格洛德最早推出简写的三角符号: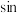 ,
,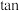 ,
, (正割),1675年,英国人奥屈特最早推出余下的简写三角符号:
(正割),1675年,英国人奥屈特最早推出余下的简写三角符号: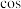 、
、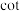 、
、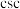 (余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用起来,其中
(余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用起来,其中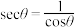 ,
,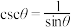 .若
.若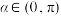 ,且
,且 ,则
,则
______ .
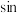 ,
,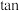 ,
, (正割),1675年,英国人奥屈特最早推出余下的简写三角符号:
(正割),1675年,英国人奥屈特最早推出余下的简写三角符号: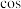 、
、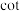 、
、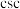 (余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用起来,其中
(余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用起来,其中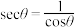 ,
,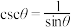 .若
.若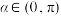 ,且
,且 ,则
,则
您最近一年使用:0次
2023-06-20更新
|
164次组卷
|
2卷引用:江苏省淮安市楚州中学、新马中学2022-2023学年高一下学期期中联考数学试题



