11-12高二下·安徽宿州·期中
名校
解题方法
1 . 将一个边长为a的正方形铁片的四角截去四个边长均为x的小正方形,做成一个无盖方盒.
(1)试把方盒的容积V表示为x的函数;
(2)x多大时,方盒的容积V最大?
(1)试把方盒的容积V表示为x的函数;
(2)x多大时,方盒的容积V最大?
您最近一年使用:0次
2021-11-21更新
|
1218次组卷
|
19卷引用:2015-2016学年山西省孝义市高二上学期期末考试文科数学试卷
2015-2016学年山西省孝义市高二上学期期末考试文科数学试卷(已下线)2011-2012学年安徽省宿州市高二下学期期中质量检测理科数学试卷(已下线)2011-2012学年福建省上杭一中高二下学期期末考试理科数学试卷(已下线)2012-2013学年广东省佛山市佛山一中高二下学期期中考试文科数学试卷(已下线)2012-2013学年广东省佛山市佛山一中高二下学期期中考试理科数学试卷河南省商丘市九校2017-2018学年高二上学期期末联考数学(文)试题广西桂林市2019-2020学年高二下学期期末质量检测数学(文)试题人教A版(2019) 选择性必修第二册 新高考名师导学 第五章 5.3 导数在研究函数中的应用海南省华中师范大学琼中附属中学2020-2021学年高二3月份考试数学试题宁夏中宁县中宁中学2020-2021学年高二下学期第一次月考数学(理)试题(A卷)广西贵港市覃塘区覃塘高级中学2020-2021学年高二3月月考数学(理)试题广西贵港市立德高级中学2020-2021学年高二3月月考数学(理)试题(已下线)5.3 导数在研究函数中的应用人教A版(2019)选择性必修第二册课本习题 习题5.3(已下线)5.3.2课时3导数在解决实际问题中的应用 第一练 练好课本试题广东省佛山市南海区九江中学2023-2024学年高二下学期4月月考数学试题【导学案】7.2实际问题中的最值问题课前预习-北师大版2019选修第二册第二章导数及其应用(已下线)第03讲 导数与函数的极值、最值(七大题型)(讲义)【课堂例】5.3.4利用导数研究二次函数 课堂例题 沪教版(2020)选择性必修第二册 第5章 导数及其应用
2 . 已知函数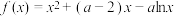 .
.
(1)当 时,
时,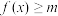 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)若 为负实数,求函数
为负实数,求函数 的单调性.
的单调性.
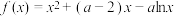 .
.(1)当
 时,
时,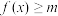 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)若
 为负实数,求函数
为负实数,求函数 的单调性.
的单调性.
您最近一年使用:0次
2021-09-01更新
|
566次组卷
|
2卷引用:山西省柳林县2020-2021学年高二下学期期中数学(理)试题
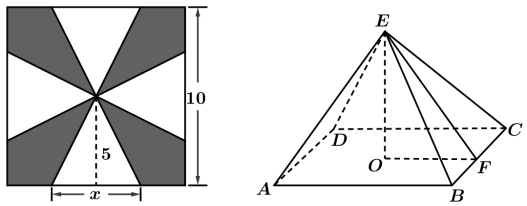
3 . 一块边长为 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥)型容器,当
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥)型容器,当 多大时,该容器的体积最大.
多大时,该容器的体积最大.
 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥)型容器,当
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥)型容器,当 多大时,该容器的体积最大.
多大时,该容器的体积最大.
您最近一年使用:0次
2021-09-01更新
|
113次组卷
|
2卷引用:山西省柳林县2020-2021学年高二下学期期中数学(理)试题
4 . 已知函数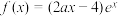 .
.
(1)讨论f(x)的单调性;
(2)当x>1时,f(x)>2(a-2)e恒成立,求a的取值范围.
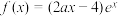 .
.(1)讨论f(x)的单调性;
(2)当x>1时,f(x)>2(a-2)e恒成立,求a的取值范围.
您最近一年使用:0次
2010·福建漳州·一模
名校
解题方法
5 . 已知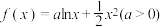 ,若对任意两个不等的正实数
,若对任意两个不等的正实数 ,
, ,都有
,都有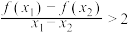 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
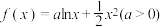 ,若对任意两个不等的正实数
,若对任意两个不等的正实数 ,
, ,都有
,都有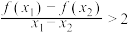 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )A.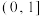 | B. | C. | D. |
您最近一年使用:0次
2020-11-12更新
|
1889次组卷
|
29卷引用:山西省吕梁市孝义市2019-2020学年高二上学期期末数学(文)试题
山西省吕梁市孝义市2019-2020学年高二上学期期末数学(文)试题河北省定州中学2017-2018学年高二上学期期末考试数学试题河南师范大学附属中学2017-2018学年高二4月月考数学(文)试题河南省八市2017-2018学年高二下学期第一次测评理科数学试题浙江省宁波市慈溪市六校2018-2019学年高二下学期期中联考数学试题江苏省扬州市宝应县2019-2020学年高二下学期期中数学试题广东省佛山市三水区三水中学2019-2020学年高二下学期第二次统考数学试题河南省新安县第一高级中学2019-2020学年高二5月月考数学(理)试题广西南宁三中2019-2020学年下学期高二期末考试(重点班)文科数学试题广西南宁三中2019-2020学年下学期高二期末考试(重点班)理科数学试题新疆生产建设兵团第四师第一中学2019-2020学年高二下学期期中考试数学(理)试题新疆生产建设兵团第四师第一中学2019-2020学年高二下学期期中考试数学(文)试题人教A版(2019) 选择性必修第二册 过关斩将 第五章 一元函数的导数及其应用 5.3 导数在研究函数中的应用 5.3.1 函数的单调性(已下线)第03章 《期中综合试卷一》(A卷基础篇)-2020-2021学年高二数学下学期同步单元AB卷(苏教版)辽宁省锦州市2020-2021学年高二下学期期末数学试题广东省佛山市华附南海实验高中2020-2021学年高二下学期期中数学试题安徽省六安市第一中学2020-2021学年高二下学期第一次阶段检测理科数学试题第1章 导数及其应用 单元测试(已下线)2010年福建省漳州一中高三毕业班质量检查数学试题(理)2017届安徽合肥一中高三上学期月考一数学(文)试卷(已下线)二轮复习 【理】专题4 导数及其应用 押题专练【市级联考】河南省濮阳市2019届高三下学期摸底考试数学(理)试题福建省泉州市惠安县第十六中学2019-2020学年高三上学期期中数学(理)试题福建省泉州市惠安县第十六中学2020届高三上学期期中数学(文)试题(已下线)专题4.2 应用导数研究函数的单调性(精讲)-2021年新高考数学一轮复习学与练(已下线)专题3.2 导数与函数的单调性-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破(已下线)专题三 能力提升检测卷 (测)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)3.4 函数的单调性(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)易错点07 导数及其应用
解题方法
6 . 设函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)若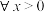 ,
, 成立,求
成立,求 的取值范围.
的取值范围.
 ,其中
,其中 .
.(1)当
 时,求函数
时,求函数 的极值;
的极值;(2)若
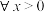 ,
, 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
7 . 已知函数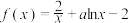 (
( ).
).
(1)若曲线 在点
在点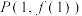 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;
(2)若对于任意 ,都有
,都有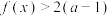 成立,试求a的取值范围.
成立,试求a的取值范围.
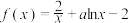 (
( ).
).(1)若曲线
 在点
在点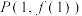 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;(2)若对于任意
 ,都有
,都有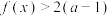 成立,试求a的取值范围.
成立,试求a的取值范围.
您最近一年使用:0次
名校
8 . 已知函数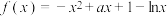 .
.
(1)若 在
在 处取到极值,求函数
处取到极值,求函数 的单调区间;
的单调区间;
(2)若 在
在 恒成立,求
恒成立,求 的范围.
的范围.
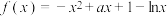 .
.(1)若
 在
在 处取到极值,求函数
处取到极值,求函数 的单调区间;
的单调区间;(2)若
 在
在 恒成立,求
恒成立,求 的范围.
的范围.
您最近一年使用:0次
2020-02-27更新
|
586次组卷
|
6卷引用:山西省汾阳市汾阳中学2020-2021学年高二下学期开学考试数学(文) 试题
名校
9 . 已知函数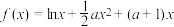 .
.
(1)讨论函数 的单调性;
的单调性;
(2)设函数 图象上不重合的两点
图象上不重合的两点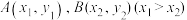 .证明:
.证明: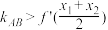 .(
.(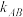 是直线
是直线 的斜率)
的斜率)
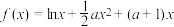 .
.(1)讨论函数
 的单调性;
的单调性;(2)设函数
 图象上不重合的两点
图象上不重合的两点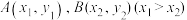 .证明:
.证明: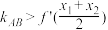 .(
.(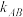 是直线
是直线 的斜率)
的斜率)
您最近一年使用:0次
2020-02-01更新
|
1338次组卷
|
10卷引用:山西省吕梁市孝义市2022-2023学年高二上学期期末数学试题
山西省吕梁市孝义市2022-2023学年高二上学期期末数学试题山东省济宁市2019-2020学年高二上学期期末数学试题人教A版(2019) 选择性必修第二册 过关斩将 第五章 一元函数的导数及其应用 本章达标检测(已下线)第一章 章末复习课-2020-2021学年高二数学(理)课时同步练(人教A版选修2-2)福建省晋江市第一中学2020-2021学年高二下学期期中考数学试题(已下线)第05章 章末复习课-2020-2021学年高二数学课时同步练(人教A版选择性必修第二册)2023版 湘教版(2019) 选修第二册 过关斩将 第1章 导数及其应用(已下线)第5章一元函数的导数及其应用(单元测试)四川省绵阳南山中学2021-2022学年高二下学期4月月考数学(文)试题(已下线)重难点突破06 双变量问题(六大题型)
10 . 已知函数f(x)=2xlnx+1.
(1)求曲线y=f(x)在点(e,f(e))处的切线方程;
(2)若关于x的不等式f(x) x2+ax在(
x2+ax在( ,+∞)上恒成立,求实数a的取值范围.
,+∞)上恒成立,求实数a的取值范围.
(1)求曲线y=f(x)在点(e,f(e))处的切线方程;
(2)若关于x的不等式f(x)
 x2+ax在(
x2+ax在( ,+∞)上恒成立,求实数a的取值范围.
,+∞)上恒成立,求实数a的取值范围.
您最近一年使用:0次



