名校
1 . 已知函数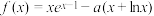 ,
, .
.
(1)当 时,求函数
时,求函数 的单减区间;
的单减区间;
(2)若 存在极小值,求实数
存在极小值,求实数 的取值范围;
的取值范围;
(3)设 是
是 的极小值点,且
的极小值点,且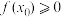 ,证明:
,证明: .
.
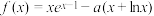 ,
, .
.(1)当
 时,求函数
时,求函数 的单减区间;
的单减区间;(2)若
 存在极小值,求实数
存在极小值,求实数 的取值范围;
的取值范围;(3)设
 是
是 的极小值点,且
的极小值点,且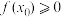 ,证明:
,证明: .
.
您最近半年使用:0次
2020-11-23更新
|
1416次组卷
|
5卷引用:天津市第一中学2020-2021学年高三上学期月考(一)数学试题
解题方法
2 . 已知函数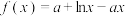 ,且
,且 恒成立.
恒成立.
(1)求实数 的值;
的值;
(2)记 ,若
,若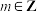 ,且当
,且当 时,不等式
时,不等式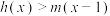 恒成立,求
恒成立,求 的最大值.
的最大值.
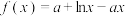 ,且
,且 恒成立.
恒成立.(1)求实数
 的值;
的值;(2)记
 ,若
,若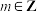 ,且当
,且当 时,不等式
时,不等式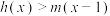 恒成立,求
恒成立,求 的最大值.
的最大值.
您最近半年使用:0次
名校
3 . 已知函数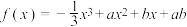 .
.
(1)若 是奇函数,且有三个零点,求
是奇函数,且有三个零点,求 的取值范围;
的取值范围;
(2)若 在
在 处有极大值
处有极大值 ,求当
,求当 时
时 的值域.
的值域.
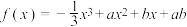 .
.(1)若
 是奇函数,且有三个零点,求
是奇函数,且有三个零点,求 的取值范围;
的取值范围;(2)若
 在
在 处有极大值
处有极大值 ,求当
,求当 时
时 的值域.
的值域.
您最近半年使用:0次
2020-11-22更新
|
608次组卷
|
6卷引用:山东省临沂市2020-2021学年高三上学期期中考试数学试题
名校
解题方法
4 . 已知函数 在x=1处取得极值-6.
在x=1处取得极值-6.
(1)求实数a,b的值;
(2)求函数f(x)在区间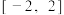 上的最大值和最小值.
上的最大值和最小值.
 在x=1处取得极值-6.
在x=1处取得极值-6. (1)求实数a,b的值;
(2)求函数f(x)在区间
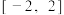 上的最大值和最小值.
上的最大值和最小值.
您最近半年使用:0次
20-21高三上·江西南昌·阶段练习
名校
5 . 函数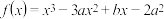 在
在 时有极值0,那么
时有极值0,那么 的值为( )
的值为( )
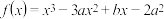 在
在 时有极值0,那么
时有极值0,那么 的值为( )
的值为( )| A.14 | B.40 | C.48 | D.14或40 |
您最近半年使用:0次
2020-11-21更新
|
1102次组卷
|
5卷引用:【南昌新东方】江西省南昌三中2020-2021学年高三上学期11月第一次月考数学(理)试题24
(已下线)【南昌新东方】江西省南昌三中2020-2021学年高三上学期11月第一次月考数学(理)试题24江苏省南通市海门市包场高级中学2020-2021学年高二上学期12月学情调查数学试题江西省南昌市第三中学2021届高三上学期第四次月考考试数学试题新疆哈密市第一中学2021-2022 学年高二下学期期中考数学试题(文科)江苏省扬州市邗江区第一中学2022-2023学年高二下学期5月月考数学试题
名校
解题方法
6 . 已知 为正实数,若函数
为正实数,若函数 的极小值为0,则
的极小值为0,则 的值为
的值为_____
 为正实数,若函数
为正实数,若函数 的极小值为0,则
的极小值为0,则 的值为
的值为
您最近半年使用:0次
2020-11-19更新
|
777次组卷
|
5卷引用:陕西省咸阳市高新一中2020-2021学年高三上学期期中质量检测文科数学试题
陕西省咸阳市高新一中2020-2021学年高三上学期期中质量检测文科数学试题(已下线)专题5.3 导数在研究函数中的应用(2)(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)专题6.3 导数与函数的极值、最值(B卷提升篇)-2020-2021学年高二数学选择性必修第三册同步单元AB卷(新教材人教B版)江苏省苏州市常熟市2020-2021学年高二下学期期中数学试题陕西省咸阳市武功县普集高中2021-2022学年高三上学期期末理科数学试题
名校
解题方法
7 . 已知函数 的极值为
的极值为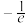 .
.
(1)求 的值并求函数
的值并求函数 在
在 处的切线方程;
处的切线方程;
(2)已知函数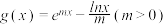 ,存在
,存在 ,使得
,使得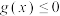 成立,求
成立,求 得最大值.
得最大值.
 的极值为
的极值为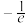 .
.(1)求
 的值并求函数
的值并求函数 在
在 处的切线方程;
处的切线方程;(2)已知函数
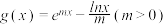 ,存在
,存在 ,使得
,使得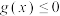 成立,求
成立,求 得最大值.
得最大值.
您最近半年使用:0次
2020-11-16更新
|
393次组卷
|
4卷引用:福建省福州市八县(市)一中2021届高三上学期期中联考数学试题
名校
解题方法
8 . 已知函数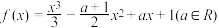 .
.
(1)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)当 时,
时,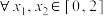 ,
,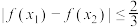 恒成立,求
恒成立,求 的取值范围.
的取值范围.
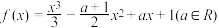 .
.(1)若
 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;(2)当
 时,
时,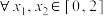 ,
,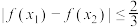 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
9 . 已知函数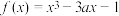 在
在 处取得极值.
处取得极值.
(1)求实数a的值.
(2)当 时,求函数
时,求函数 的最小值.
的最小值.
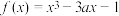 在
在 处取得极值.
处取得极值.(1)求实数a的值.
(2)当
 时,求函数
时,求函数 的最小值.
的最小值.
您最近半年使用:0次
2020-11-08更新
|
402次组卷
|
5卷引用:四川省泸州高级中学2020-2021学年高三上学期9月月考文科数学试题
四川省泸州高级中学2020-2021学年高三上学期9月月考文科数学试题(已下线)调研测试三(A卷 基础过关检测)-2021年高考数学(文)一轮复习单元滚动双测卷(已下线)专题21 函数与导数综合——2020年高考数学母题题源解密(山东、海南专版)江苏省苏州实验中学2020-2021学年高二下学期3月月考数学试题(已下线)第五章 导数及其应用A卷(基础过关)-【双基双测】2021-2022学年高二数学同步单元AB卷(苏教版2019选择性必修第一册)
名校
解题方法
10 . 请写出一个使得函数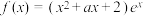 既有极大值又有极小值的实数a的值
既有极大值又有极小值的实数a的值___________ .
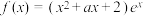 既有极大值又有极小值的实数a的值
既有极大值又有极小值的实数a的值
您最近半年使用:0次
2020-11-07更新
|
1006次组卷
|
7卷引用:北京实验学校(海淀)2019-2020 学年度高二下学期期末考试数学试题
北京实验学校(海淀)2019-2020 学年度高二下学期期末考试数学试题广东省阳春市第一中学2022届高三上学期10月月考数学试题(已下线)第13练 利用导数研究函数极值-2022年【寒假分层作业】高二数学(苏教版2019选择性必修第一册)(已下线)专题5.3 利用导数研究函数的极值-2021-2022学年高二数学特色专题卷(人教A版2019选择性必修第二册)(已下线)期末测试卷01(B卷·提升能力)-2021-2022学年高二数学同步单元AB卷(苏教版2019选择性必修第一册)【学科网名师堂】(已下线)第24讲 章末检测四-备战2023年高考数学一轮复习考点帮(新高考专用)第5章 导数及其应用(培优卷)-【满分计划】2022-2023学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)



