2024·全国·模拟预测
1 . 已知函数 .
.
(1)若曲线 在
在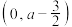 处的切线方程为
处的切线方程为 ,求
,求 的值及
的值及 的单调区间.
的单调区间.
(2)若 的极大值为
的极大值为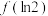 ,求
,求 的取值范围.
的取值范围.
(3)当 时,求证:
时,求证: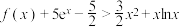 .
.
 .
.(1)若曲线
 在
在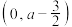 处的切线方程为
处的切线方程为 ,求
,求 的值及
的值及 的单调区间.
的单调区间.(2)若
 的极大值为
的极大值为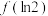 ,求
,求 的取值范围.
的取值范围.(3)当
 时,求证:
时,求证: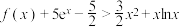 .
.
您最近一年使用:0次
名校
2 . 设函数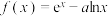 .
.
(1)若 ,讨论
,讨论 的单调性;
的单调性;
(2)若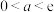 ,证明:在区间
,证明:在区间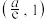 内,
内, 存在唯一的极小值点
存在唯一的极小值点 ,且
,且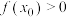 .
.
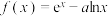 .
.(1)若
 ,讨论
,讨论 的单调性;
的单调性;(2)若
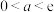 ,证明:在区间
,证明:在区间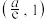 内,
内, 存在唯一的极小值点
存在唯一的极小值点 ,且
,且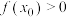 .
.
您最近一年使用:0次
名校
解题方法
3 . 有两个条件:(1)函数 的图象过点
的图象过点 ,且函数
,且函数 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数.(2)
上是增函数.(2) 在
在 时取得极大值
时取得极大值 .这两个条件中,请选择一个合适的条件将下面的题目补充完整(只要填写序号),并解答本题.题目:已知函数
.这两个条件中,请选择一个合适的条件将下面的题目补充完整(只要填写序号),并解答本题.题目:已知函数 存在极值,并且______.
存在极值,并且______.
(1)求 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的最值
的最值
 的图象过点
的图象过点 ,且函数
,且函数 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数.(2)
上是增函数.(2) 在
在 时取得极大值
时取得极大值 .这两个条件中,请选择一个合适的条件将下面的题目补充完整(只要填写序号),并解答本题.题目:已知函数
.这两个条件中,请选择一个合适的条件将下面的题目补充完整(只要填写序号),并解答本题.题目:已知函数 存在极值,并且______.
存在极值,并且______.(1)求
 的解析式;
的解析式;(2)当
 时,求函数
时,求函数 的最值
的最值
您最近一年使用:0次
名校
解题方法
4 . 函数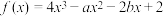 在
在 处有极小值
处有极小值 ,则
,则 的值等于( )
的值等于( )
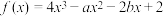 在
在 处有极小值
处有极小值 ,则
,则 的值等于( )
的值等于( )| A.0 | B. | C. | D.6 |
您最近一年使用:0次
2024·全国·模拟预测
5 . 已知函数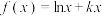 的单调递增区间为
的单调递增区间为 .
.
(1)求函数 的图象在点
的图象在点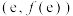 处的切线方程;
处的切线方程;
(2)若函数 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
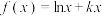 的单调递增区间为
的单调递增区间为 .
.(1)求函数
 的图象在点
的图象在点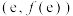 处的切线方程;
处的切线方程;(2)若函数
 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
6 . 已知函数 在
在 上无极值,则
上无极值,则 的取值范围是( )
的取值范围是( )
 在
在 上无极值,则
上无极值,则 的取值范围是( )
的取值范围是( )A. | B.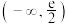 | C.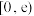 | D.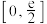 |
您最近一年使用:0次
解题方法
7 . 如果函数 在区间[a,b]上为增函数,则记为
在区间[a,b]上为增函数,则记为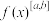 ,函数
,函数 在区间[a,b]上为减函数,则记为
在区间[a,b]上为减函数,则记为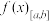 .如果
.如果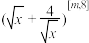 ,则实数m的最小值为
,则实数m的最小值为________ ;如果函数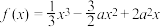 ,且
,且 ,
,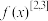 ,则实数
,则实数
________ .
 在区间[a,b]上为增函数,则记为
在区间[a,b]上为增函数,则记为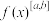 ,函数
,函数 在区间[a,b]上为减函数,则记为
在区间[a,b]上为减函数,则记为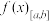 .如果
.如果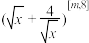 ,则实数m的最小值为
,则实数m的最小值为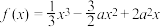 ,且
,且 ,
,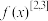 ,则实数
,则实数
您最近一年使用:0次
名校
解题方法
8 . 已知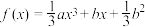 在
在 处取得极大值1,则下列结论正确的是( )
处取得极大值1,则下列结论正确的是( )
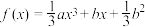 在
在 处取得极大值1,则下列结论正确的是( )
处取得极大值1,则下列结论正确的是( )A.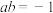 | B.对称中心为 |
C. | D.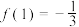 |
您最近一年使用:0次
名校
9 . 设函数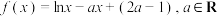 .函数
.函数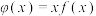
(1)当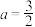 时,判断函数
时,判断函数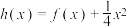 的零点个数;
的零点个数;
(2)令函数 ,求函数
,求函数 的单调区间;
的单调区间;
(3)已知函数 在
在 处取得极大值,求实数
处取得极大值,求实数 的取值范围.
的取值范围.
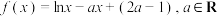 .函数
.函数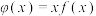
(1)当
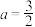 时,判断函数
时,判断函数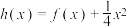 的零点个数;
的零点个数;(2)令函数
 ,求函数
,求函数 的单调区间;
的单调区间;(3)已知函数
 在
在 处取得极大值,求实数
处取得极大值,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
10 . 已知函数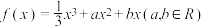 在
在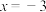 处取得极大值为9.
处取得极大值为9.
(1)求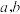 的值;
的值;
(2)求函数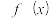 在区间
在区间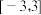 上的最大值.
上的最大值.
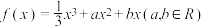 在
在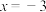 处取得极大值为9.
处取得极大值为9.(1)求
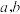 的值;
的值;(2)求函数
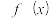 在区间
在区间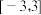 上的最大值.
上的最大值.
您最近一年使用:0次



