名校
解题方法
1 . 已知函数 ,若
,若 在
在 处取得极值10,.
处取得极值10,.
(1)求 的值;
的值;
(2)方程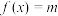 在
在 有解,求实数
有解,求实数 的范围.
的范围.
 ,若
,若 在
在 处取得极值10,.
处取得极值10,.(1)求
 的值;
的值;(2)方程
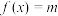 在
在 有解,求实数
有解,求实数 的范围.
的范围.
您最近半年使用:0次
2024·全国·模拟预测
2 . 已知函数 .
.
(1)若曲线 在
在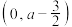 处的切线方程为
处的切线方程为 ,求
,求 的值及
的值及 的单调区间.
的单调区间.
(2)若 的极大值为
的极大值为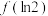 ,求
,求 的取值范围.
的取值范围.
(3)当 时,求证:
时,求证: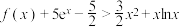 .
.
 .
.(1)若曲线
 在
在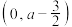 处的切线方程为
处的切线方程为 ,求
,求 的值及
的值及 的单调区间.
的单调区间.(2)若
 的极大值为
的极大值为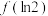 ,求
,求 的取值范围.
的取值范围.(3)当
 时,求证:
时,求证: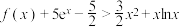 .
.
您最近半年使用:0次
解题方法
3 . 已知函数 的最大值为1.
的最大值为1.
(1)求实数 的值;
的值;
(2)若函数 有极值,求实数
有极值,求实数 的取值范围.
的取值范围.
 的最大值为1.
的最大值为1.(1)求实数
 的值;
的值;(2)若函数
 有极值,求实数
有极值,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
4 . 已知函数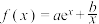 在定义域内既存在极大值点又存在极小值点,则( )
在定义域内既存在极大值点又存在极小值点,则( )
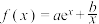 在定义域内既存在极大值点又存在极小值点,则( )
在定义域内既存在极大值点又存在极小值点,则( )A. | B.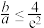 |
C.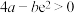 | D.对于任意非零实数 ,总存在实数 ,总存在实数 满足题意 满足题意 |
您最近半年使用:0次
名校
解题方法
5 . 若函数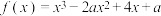 不存在极值,则
不存在极值,则 的取值范围是( )
的取值范围是( )
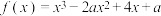 不存在极值,则
不存在极值,则 的取值范围是( )
的取值范围是( )A. | B.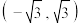 | C. | D.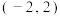 |
您最近半年使用:0次
2024-04-23更新
|
1480次组卷
|
5卷引用:山东省大联考2023-2024学年高二下学期3月质量检测联合调考数学试题
山东省大联考2023-2024学年高二下学期3月质量检测联合调考数学试题(已下线)高二 模块3 专题2 小题进阶提升练广东省佛山市顺德区镇街联考2023-2024学年高二下学期4月月考数学试题(已下线)5.3.2.1函数的极值——课后作业(基础版)安徽省淮南第二中学2023-2024学年高二下学期期中教学检测数学试题
名校
解题方法
6 . 已知函数 在
在 处取得极小值10,则
处取得极小值10,则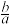 的值为
的值为 ___ .
 在
在 处取得极小值10,则
处取得极小值10,则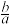 的值为
的值为
您最近半年使用:0次
9-10高二下·天津·期中
名校
解题方法
7 . 已知函数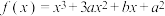 在
在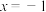 时有极值0,则
时有极值0,则
______ .
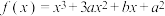 在
在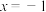 时有极值0,则
时有极值0,则
您最近半年使用:0次
2024-04-23更新
|
1324次组卷
|
54卷引用:2010年天津一中高二下学期期中考试数学(理科)试题
(已下线)2010年天津一中高二下学期期中考试数学(理科)试题(已下线)2014届江苏省灌云高级中学高三第一学期期中考试理科数学试卷2015届山西大学附属中学高三上学期期中考试文科数学试卷2014-2015学年河北省保定高阳中学高二下学期期末考试理科数学试卷2017届河北衡水中学高三上学期一调考试数学(理)试卷宁夏育才中学2016-2017学年高二下学期期中考试数学(理)试题北京西城14中2016-2017高二下学期期中数学(理)试题[市级联考】安徽省定远重点中学2019届高三上学期期中考试数学(理)试题【校级联考】辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2018-2019学年高二上学期期末考试数学(文)试题广西桂林市龙胜中学2019-2020学年高二开学考试数学(文)试题吉林省汪清县第六中学2019-2020学年高二下学期期中考试数学(理)试题甘肃省武威市第十八中学2019-2020学年高二下学期期中考试数学(理)试题江西省赣州市赣县第三中学2019-2020学年高二6月份考试数学(文)试题(已下线)5.3.2+函数的极值与导数(基础练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第二册)(已下线)3.3.2+函数的极值与导数(基础练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-1)安徽省宿州市十三所省重点中学2020-2021学年高二上学期期末数学(文)试题(已下线)5.3.2 函数的极值与最大(小)值(1)B提高练(已下线)1.3.2 函数的极值与导数(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)天津市南开中学2020-2021学年高二下学期期中数学试题(已下线)单元卷 导数及其应用(基础卷)-2020-2021学年高二数学课时同步练(苏教版选修1-1)(已下线)6.2.2 导数与函数的极值、最值 (1) -B提高练 陕西省渭南市大荔县2020-2021学年高二下学期期末文科数学试题(已下线)专题3.6 利用导数研究函数的极值、最值-重难点题型精练-2022年高考数学一轮复习举一反三系列(新高考地区专用)山东省滨州市2021-2022学年高二上学期期末数学试题陕西省西安市鄠邑区2021-2022学年高二下学期期末理科数学试题2023版 湘教版(2019) 选修第二册 过关斩将 第1章 1.3.2 函数的极值与导数河南省南阳市第一中学校2022-2023学年高三上学期第二次阶段考试文科数学试题河南省信阳市固始县高级中学第一中学2022-2023学年高三上学期教学质量检测文科数学试题四川省绵阳南山中学2022-2023学年高三上学期11月月考理科数学试题(已下线)模拟卷03上海市嘉定区封浜高级中学2023届高三上学期期中数学试题(已下线)第五章 一元函数的导数及其应用 讲核心 02第五章 一元函数的导数及其应用 (单元测)(已下线)第5章 导数及其应用(A卷·知识通关练)(3)(已下线)5.3.2~5.3.3 极大值与极小值、最大值与最小值 (1)上海市七宝中学2023届高三下学期开学考试数学试题福建省诏安县桥东中学(霞葛教学点)2022-2023学年高二下学期第一次月考数学试题(已下线)第65练 计算提升训练5天津市天津中学2022-2023学年高一下学期第一次月考数学试题四川省江油中学2022-2023学年高二下学期期中考试数学(文)试题(已下线)第三节 导数与函数的极值、最值(核心考点集训)安徽省池州市贵池区2022-2023学年高二下学期期中考试数学试题(已下线)高二下期中真题精选(基础60题专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)新疆维吾尔自治区喀什地区巴楚县第一中学2022-2023学年高二下学期期中数学试题(已下线)考点17 导数的应用--函数极值问题 2024届高考数学考点总动员【练】河南省信阳高级中学2023届高三二轮复习滚动测试8文科数学试题(已下线)5.3导数在研究函数中的应用(2)(已下线)专题10 导数12种常见考法归类(3)(已下线)第五章 导数及其应用(知识归纳+题型突破)(3)天津市天津大学附属中学2023-2024学年高二下学期3月月考数学试卷北京市第一七一中学2023-2024学年高二下学期3月月考数学试题山东省临沂市第二十四中学2023-2024学年高二下学期3月月考数学试题广东省东莞高级中学2023-2024学年高二下学期4月月考数学试题(已下线)5.3.2.1函数的极值——课后作业(提升版)
名校
8 . 已知函数 有极值,则a的取值范围是
有极值,则a的取值范围是____________ .
 有极值,则a的取值范围是
有极值,则a的取值范围是
您最近半年使用:0次
名校
解题方法
9 . 已知函数 在
在 处取得极值5,则
处取得极值5,则
____ .
 在
在 处取得极值5,则
处取得极值5,则
您最近半年使用:0次
2024-04-22更新
|
506次组卷
|
4卷引用:四川省遂宁市射洪中学2023-2024学年高二下学期第一次半月考数学试题
10 . 设函数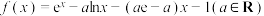 ,
, 有唯一极值点
有唯一极值点 .
.
(1)证明: ;
;
(2)若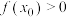 ,求
,求 的取值范围;
的取值范围;
(3)若 的图象上不存在关于直线
的图象上不存在关于直线 对称的两点,证明:
对称的两点,证明: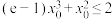 .
.
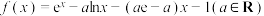 ,
, 有唯一极值点
有唯一极值点 .
.(1)证明:
 ;
;(2)若
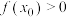 ,求
,求 的取值范围;
的取值范围;(3)若
 的图象上不存在关于直线
的图象上不存在关于直线 对称的两点,证明:
对称的两点,证明: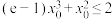 .
.
您最近半年使用:0次



