2024高二下·全国·专题练习
解题方法
1 . 若函数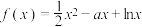 在
在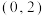 上有极值,则实数
上有极值,则实数 的取值范围是
的取值范围是_______ .
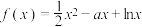 在
在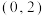 上有极值,则实数
上有极值,则实数 的取值范围是
的取值范围是
您最近半年使用:0次
解题方法
2 .  ,函数
,函数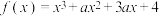 没有极值的充要条件为
没有极值的充要条件为______ .
 ,函数
,函数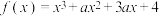 没有极值的充要条件为
没有极值的充要条件为
您最近半年使用:0次
名校
3 . 若函数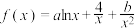 (
( )既有极大值也有极小值,则下列结论一定正确的是( )
)既有极大值也有极小值,则下列结论一定正确的是( )
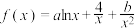 (
( )既有极大值也有极小值,则下列结论一定正确的是( )
)既有极大值也有极小值,则下列结论一定正确的是( )A. | B. | C.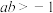 | D.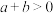 |
您最近半年使用:0次
2024-03-21更新
|
1404次组卷
|
3卷引用:广东省佛山市禅城区2024届高三统一调研测试(二)数学试题
广东省佛山市禅城区2024届高三统一调研测试(二)数学试题(已下线)2.6 导数及其应用(极值问题、最值问题)(高考真题素材之十年高考)山东省东明县第一中学2023-2024学年高二下学期第一次(4月)月考数学试题
2024高三·全国·专题练习
解题方法
4 . 已知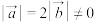 ,且关于x的函数
,且关于x的函数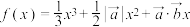 在R上有两个极值,则向量
在R上有两个极值,则向量 与
与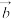 的夹角的范围是
的夹角的范围是________ .
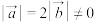 ,且关于x的函数
,且关于x的函数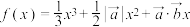 在R上有两个极值,则向量
在R上有两个极值,则向量 与
与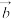 的夹角的范围是
的夹角的范围是
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
5 . 求下列函数的解析式
(1)已知 ,则
,则
________ .
(2)已知 是三次函数,且在
是三次函数,且在 处的极值为0,在
处的极值为0,在 处的极值为1,则
处的极值为1,则
______ .
(3)已知 的定义域为
的定义域为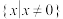 ,满足
,满足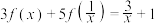 ,则函数
,则函数
________ .
(4)已知函数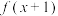 是偶函数,且
是偶函数,且 时
时 ,则
,则 时,
时,
________ .
(1)已知
 ,则
,则
(2)已知
 是三次函数,且在
是三次函数,且在 处的极值为0,在
处的极值为0,在 处的极值为1,则
处的极值为1,则
(3)已知
 的定义域为
的定义域为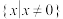 ,满足
,满足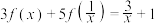 ,则函数
,则函数
(4)已知函数
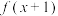 是偶函数,且
是偶函数,且 时
时 ,则
,则 时,
时,
您最近半年使用:0次
名校
解题方法
6 . 已知函数 .
.
(1)若函数 无极值,求实数
无极值,求实数 的取值范围;
的取值范围;
(2)若关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 无极值,求实数
无极值,求实数 的取值范围;
的取值范围;(2)若关于
 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024-03-12更新
|
440次组卷
|
2卷引用:高三理数试题-河南省豫南六校2022-2023学年高三上学期第一次联考试题
7 . 已知函数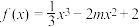 ,其中
,其中 .
.
(1)若 的极小值为
的极小值为 ,求
,求 单调增区间;
单调增区间;
(2)讨论 的零点个数.
的零点个数.
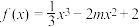 ,其中
,其中 .
.(1)若
 的极小值为
的极小值为 ,求
,求 单调增区间;
单调增区间;(2)讨论
 的零点个数.
的零点个数.
您最近半年使用:0次
名校
8 . 已知函数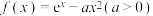 .
.
(1)若函数 有3个不同的零点,求a的取值范围;
有3个不同的零点,求a的取值范围;
(2)已知 为函数
为函数 的导函数,
的导函数, 在
在 上有极小值0,对于某点
上有极小值0,对于某点 ,
, 在P点的切线方程为
在P点的切线方程为 ,若对于
,若对于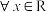 ,都有
,都有 ,则称P为好点.
,则称P为好点.
①求a的值;
②求所有的好点.
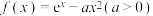 .
.(1)若函数
 有3个不同的零点,求a的取值范围;
有3个不同的零点,求a的取值范围;(2)已知
 为函数
为函数 的导函数,
的导函数, 在
在 上有极小值0,对于某点
上有极小值0,对于某点 ,
, 在P点的切线方程为
在P点的切线方程为 ,若对于
,若对于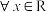 ,都有
,都有 ,则称P为好点.
,则称P为好点.①求a的值;
②求所有的好点.
您最近半年使用:0次
2024-03-08更新
|
1213次组卷
|
4卷引用:河北省部分学校联考2024届高三下学期3月模拟(二)数学试题
9 . 设函数 .
.
(1)若 ,求函数
,求函数 图象在
图象在 处的切线方程;
处的切线方程;
(2)若 在
在 处取得极小值,求
处取得极小值,求 的单调区间;
的单调区间;
(3)若 恰有三个零点,求
恰有三个零点,求 的取值范围.
的取值范围.
 .
.(1)若
 ,求函数
,求函数 图象在
图象在 处的切线方程;
处的切线方程;(2)若
 在
在 处取得极小值,求
处取得极小值,求 的单调区间;
的单调区间;(3)若
 恰有三个零点,求
恰有三个零点,求 的取值范围.
的取值范围.
您最近半年使用:0次
名校
10 . 已知函数 .若过原点可作函数的三条切线,则( )
.若过原点可作函数的三条切线,则( )
 .若过原点可作函数的三条切线,则( )
.若过原点可作函数的三条切线,则( )A.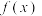 恰有2个异号极值点 恰有2个异号极值点 | B.若 ,则 ,则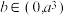 |
C.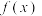 恰有2个异号零点 恰有2个异号零点 | D.若 ,则 ,则 |
您最近半年使用:0次
2024-03-07更新
|
503次组卷
|
2卷引用:2024届高三新高考改革数学适应性练习(5)(九省联考题型)



