2024·全国·模拟预测
解题方法
1 . 已知函数 在区间
在区间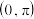 上存在两个极值点
上存在两个极值点 ,
, .
.
(1)求实数a的取值范围;
(2)若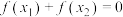 ,求证:
,求证: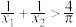 .
.
 在区间
在区间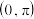 上存在两个极值点
上存在两个极值点 ,
, .
.(1)求实数a的取值范围;
(2)若
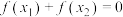 ,求证:
,求证: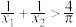 .
.
您最近半年使用:0次
2 . 已知函数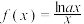 的极值为
的极值为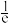 .
.
(1)求 的值;
的值;
(2)若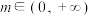 ,判断方程
,判断方程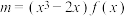 是否恒有解.
是否恒有解.
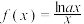 的极值为
的极值为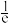 .
.(1)求
 的值;
的值;(2)若
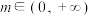 ,判断方程
,判断方程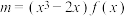 是否恒有解.
是否恒有解.
您最近半年使用:0次
名校
解题方法
3 . 已知函数 在其定义域
在其定义域 内既有极大值也有极小值,则实数
内既有极大值也有极小值,则实数 的取值范围是( )
的取值范围是( )
 在其定义域
在其定义域 内既有极大值也有极小值,则实数
内既有极大值也有极小值,则实数 的取值范围是( )
的取值范围是( )A.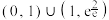 | B. | C.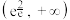 | D.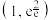 |
您最近半年使用:0次
2024-01-10更新
|
675次组卷
|
7卷引用:2020届山东省青岛二中高三上学期10月月考数学试题
2020届山东省青岛二中高三上学期10月月考数学试题四川省绵阳市2018-2019学年高二下学期期末数学(文)试题四川省绵阳市2018-2019学年高二下学期期末数学(理)试题江苏省启东市东南中学2023-2024学年高二上学期第二次质量检测数学试卷江苏省盐城市阜宁中学2023-2024学年高二上学期期末数学试卷(已下线)5.3.2课时1函数的极值 第三练 能力提升拔高(已下线)专题 6 根据极值情况求参数范围
4 . (1)讨论 的单调性;
的单调性;
(2)记 ,试探究是否存在
,试探究是否存在 使
使 在
在 处取得极小值且
处取得极小值且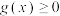 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的单调性;
的单调性;(2)记
 ,试探究是否存在
,试探究是否存在 使
使 在
在 处取得极小值且
处取得极小值且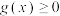 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近半年使用:0次
名校
解题方法
5 . 若函数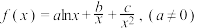 既有极大值也有极小值,则( )
既有极大值也有极小值,则( )
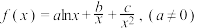 既有极大值也有极小值,则( )
既有极大值也有极小值,则( )A.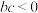 | B.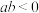 |
C.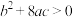 | D.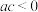 |
您最近半年使用:0次
2023-12-31更新
|
710次组卷
|
4卷引用:河北省衡水市第十三中学2024届高三上学期质检三考试数学试题
河北省衡水市第十三中学2024届高三上学期质检三考试数学试题湖北省荆州市公安县车胤中学2024届高三上学期质检模拟数学试题(一)(已下线)5.3.2 函数的极值与最大(小)值(分层练习)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第二册)(已下线)专题1.4 利用导数研究函数的极值和最值(八个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
解题方法
6 . 若函数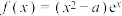 在区间
在区间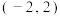 内只有极小值,无极大值,则实数
内只有极小值,无极大值,则实数 的取值范围是
的取值范围是__________ .
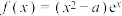 在区间
在区间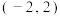 内只有极小值,无极大值,则实数
内只有极小值,无极大值,则实数 的取值范围是
的取值范围是
您最近半年使用:0次
名校
解题方法
7 . 已知函数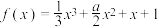 在
在 ,
, 上为增函数,在(1,2)上为减函数,则实数a的取值范围为( )
上为增函数,在(1,2)上为减函数,则实数a的取值范围为( )
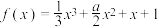 在
在 ,
, 上为增函数,在(1,2)上为减函数,则实数a的取值范围为( )
上为增函数,在(1,2)上为减函数,则实数a的取值范围为( )A.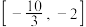 | B. | C. | D.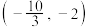 |
您最近半年使用:0次
2023-12-27更新
|
1434次组卷
|
19卷引用:湖北省新高考联考协作体2020-2021学年高二下学期期中联考数学试题
湖北省新高考联考协作体2020-2021学年高二下学期期中联考数学试题第六章 导数及其应用(A基础卷)-新教材2020-2021学年高二数学尖子生培优AB卷(人教B版2019选择性必修第三册)(已下线)考点02 导数与函数的单调性-2022年高考数学(文)一轮复习小题多维练(全国通用)人教B版(2019) 选修第三册 必杀技 第六章 6.2.1 导数与函数的单调性陕西省咸阳市武功县普集高中2022届高三加强班下学期3月月考理科数学试题(已下线)查补易混易错点03 函数与导数的基本性质-【查漏补缺】2022年高考数学(文)三轮冲刺过关(已下线)第05节 函数的基本性质(好题帮)-备战2023年高考数学一轮复习考点帮(全国通用)(已下线)8.4 单调性(精练)山东省济宁市梁山现代高级中学2021-2022学年高二下学期3月月考数学试题新疆维吾尔自治区乌鲁木齐市新疆生产建设兵团第二中学2022-2023学年高二下学期第二次月考数学试题(已下线)第02讲 单调性问题(六大题型)(讲义)河南省焦作市第十一中学2022-2023学年高二下学期期末考试数学试题(已下线)专题04 函数的极值与最大(小)值 (十二大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第09讲:一元函数的导数及其应用 (必刷7大考题+7大题型) -2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)(已下线)第5.3.2讲 函数的极值(第1课时)-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二册)(已下线)第五章 一元函数的导数及其应用章末综合达标卷-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二、三册)河北省保定市河北定州中学2023-2024学年高二下学期3月月考数学试题山东省泰安市新泰第一中学老校区(新泰中学)2023-2024学年高二下学期第一次月考数学试题江西省宜春市宜丰中学2023-2024学年高一下学期3月月考数学试题(创新部)
8 . 已知函数 ,函数
,函数 的两相邻对称中心之间的距离为1,且
的两相邻对称中心之间的距离为1,且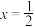 为函数
为函数 的一个极大值点.若方程
的一个极大值点.若方程 在
在 上的所有根之和等于2024,则满足条件中整数
上的所有根之和等于2024,则满足条件中整数 的值构成的集合为
的值构成的集合为________
 ,函数
,函数 的两相邻对称中心之间的距离为1,且
的两相邻对称中心之间的距离为1,且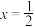 为函数
为函数 的一个极大值点.若方程
的一个极大值点.若方程 在
在 上的所有根之和等于2024,则满足条件中整数
上的所有根之和等于2024,则满足条件中整数 的值构成的集合为
的值构成的集合为
您最近半年使用:0次
名校
解题方法
9 . 已知函数 ,
, .
.
(1)求证: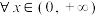 ,
,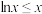 恒成立;
恒成立;
(2)若 存在极值,求a的取值范围;
存在极值,求a的取值范围;
(3)若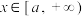 时,
时, 成立,求a的取值范围.
成立,求a的取值范围.
 ,
, .
.(1)求证:
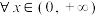 ,
,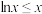 恒成立;
恒成立;(2)若
 存在极值,求a的取值范围;
存在极值,求a的取值范围;(3)若
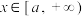 时,
时, 成立,求a的取值范围.
成立,求a的取值范围.
您最近半年使用:0次
解题方法
10 . 已知函数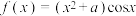 ,若
,若 是
是 的极大值点,则a的取值范围是
的极大值点,则a的取值范围是__________ .
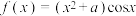 ,若
,若 是
是 的极大值点,则a的取值范围是
的极大值点,则a的取值范围是
您最近半年使用:0次



