名校
解题方法
1 . 已知函数 在
在 处取得极大值2.
处取得极大值2.
(1)求 的解析式;
的解析式;
(2)求 在
在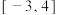 上的最值.
上的最值.
 在
在 处取得极大值2.
处取得极大值2.(1)求
 的解析式;
的解析式;(2)求
 在
在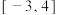 上的最值.
上的最值.
您最近半年使用:0次
2024-01-29更新
|
476次组卷
|
3卷引用:江苏省盐城市盐城中学2023-2024学年高二上学期期末数学试题
江苏省盐城市盐城中学2023-2024学年高二上学期期末数学试题河北省石家庄二十七中2023-2024学年高二下学期第一次月考数学试题(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》B提升卷(苏教版)
2 . 已知函数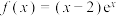 .
.
(1)求曲线 在点
在点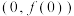 处的切线方程;
处的切线方程;
(2)设函数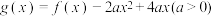 .
.
①若 在
在 处取得极大值,求
处取得极大值,求 的单调区间;
的单调区间;
②若 恰有三个零点,求
恰有三个零点,求 的取值范围.
的取值范围.
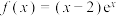 .
.(1)求曲线
 在点
在点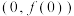 处的切线方程;
处的切线方程;(2)设函数
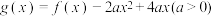 .
.①若
 在
在 处取得极大值,求
处取得极大值,求 的单调区间;
的单调区间;②若
 恰有三个零点,求
恰有三个零点,求 的取值范围.
的取值范围.
您最近半年使用:0次
名校
3 . 已知函数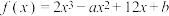 在
在 处取得极小值5.
处取得极小值5.
(1)求实数a,b的值;
(2)当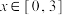 时,求函数
时,求函数 的最小值.
的最小值.
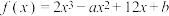 在
在 处取得极小值5.
处取得极小值5.(1)求实数a,b的值;
(2)当
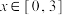 时,求函数
时,求函数 的最小值.
的最小值.
您最近半年使用:0次
2024-01-24更新
|
3915次组卷
|
13卷引用:江苏省扬州市2023-2024学年高二上学期1月期末数学试题
江苏省扬州市2023-2024学年高二上学期1月期末数学试题江西省南昌市第二中学2024届高三“九省联考”考后适应性测试数学试题(四)(已下线)第六章:导数及其应用(单元测试)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)黄金卷03(2024新题型)江苏省南京市临江高级中学2023-2024学年高二下学期期初考试数学试卷山东省威海市乳山市银滩高级中学2023-2024学年高二下学期3月月考数学试题重庆市松树桥中学校2023-2024学年高二下学期第一次月考数学试题天津市和平区天津市第一中学2023-2024学年高二下学期3月月考数学试题四川省成都市第七中学(高新校区)2023-2024学年高二下学期尖子生4月月考数学试卷四川省达州外国语学校2023-2024学年高二下学期3月月考数学试题云南省曲靖市师宗县平高中学(第四中学)2023-2024学年高二下学期3月月考数学试题卷天津市嘉诚中学2023-2024学年高二下学期第一次月考数学试卷河北省衡水市枣强中学2023-2024学年高二下学期第一次调研考试数学试题
解题方法
4 . 已知函数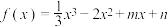 在
在 时取得极值.
时取得极值.
(1)求实数 的值;
的值;
(2)若对于任意的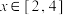 ,
,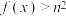 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
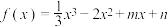 在
在 时取得极值.
时取得极值.(1)求实数
 的值;
的值;(2)若对于任意的
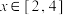 ,
,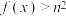 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024-01-24更新
|
2699次组卷
|
7卷引用:山西省大同市2023-2024学年高二上学期期末质量监测数学试题
山西省大同市2023-2024学年高二上学期期末质量监测数学试题2024届高三新改革适应性模拟测试数学试卷一(九省联考题型)(已下线)第五章 一元函数的导数及其应用章末综合达标卷-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)2.6.2函数的极值(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)第六章:导数及其应用(单元测试)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)信息必刷卷03福建省厦门市国贸协和双语高级中学2023-2024学年高二下学期第一次月考数学试卷
5 . 已知函数 (
( 为自然常数),
为自然常数), 为实数.
为实数.
(1)若
 在
在 上存在极值,求
上存在极值,求 的取值范围;
的取值范围;(2)若对任意
 ,
,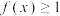 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
6 . 已知函数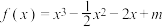 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 有三个不同的零点,求实数m的取值范围.
有三个不同的零点,求实数m的取值范围.
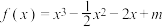 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若函数
 有三个不同的零点,求实数m的取值范围.
有三个不同的零点,求实数m的取值范围.
您最近半年使用:0次
2024-01-23更新
|
719次组卷
|
2卷引用:江苏省南京市江宁区2023-2024学年高二上学期期末统考数学试卷
解题方法
7 . 已知函数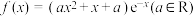 .
.
(1)若 ,函数
,函数 的极大值为
的极大值为 ,求实数a的值;
,求实数a的值;
(2)若对任意的 ,
,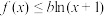 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
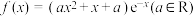 .
.(1)若
 ,函数
,函数 的极大值为
的极大值为 ,求实数a的值;
,求实数a的值;(2)若对任意的
 ,
,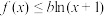 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
解题方法
8 . 若函数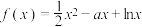 在
在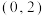 上有极值,则实数
上有极值,则实数 的取值范围是( )
的取值范围是( )
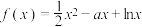 在
在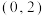 上有极值,则实数
上有极值,则实数 的取值范围是( )
的取值范围是( )A.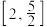 | B.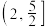 | C. | D. |
您最近半年使用:0次
名校
9 . 已知函数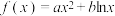 在
在 处有极值
处有极值 .
.
(1)求 、
、 的值;
的值;
(2)求出 的单调区间,并求极值.
的单调区间,并求极值.
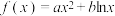 在
在 处有极值
处有极值 .
.(1)求
 、
、 的值;
的值;(2)求出
 的单调区间,并求极值.
的单调区间,并求极值.
您最近半年使用:0次
2024-01-15更新
|
2122次组卷
|
19卷引用:安徽省滁州市定远县育才学校2020-2021学年高二下学期开学考试数学(文)试题
安徽省滁州市定远县育才学校2020-2021学年高二下学期开学考试数学(文)试题重庆市朝阳中学2020-2021学年高二下学期4月月考数学试题重庆市第三十七中2020-2021学年高二下学期三月月考数学试题河北省邯郸市曲周县第一中学2020-2021学年高二下学期3月月考数学试题宁夏中卫市中宁县第一中学2022届高三上学期第一次月考数学(理)试题内蒙古海拉尔第二中学2021-2022学年高三上学期第一次阶段考数学(文科)试题河南省南阳市第六完全学校高级中学2022-2023学年高三上学期9月考试文科数学试题黑龙江省牡丹江市海林市朝鲜族中学2022-2023学年高三上学期第一次月考数学(理)试题黑龙江省牡丹江市海林市朝鲜族中学2022-2023学年高三上学期第一次月考数学(文)试题宁夏固原市第五中学2022-2023学年高二下学期第二次月考数学(理)试题福建省厦门第二中学2022-2023学年高二下学期4月月考数学试题宁夏固原市第五中学2022-2023学年高二下学期第二次月考数学(文)试题(已下线)第五章 导数及其应用(压轴题专练)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第一册)2024届高三新改革数学模拟预测训练一(九省联考题型)(已下线)FHsx1225yl181山东省青岛市即墨区第一中学2023-2024学年高二下学期第一次教学质量检测数学试题广东省深圳市翠园中学2023-2024学年高二下学期第一次段考数学试卷四川省遂宁市第一中学校2023-2024学年高二下学期3月月考试数学试题广东省东莞市第七高级中学2023-2024学年高二下学期数学第一次月考数学试题
2024·全国·模拟预测
名校
解题方法
10 . 已知函数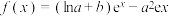 ,其中
,其中 为自然对数的底数,则( )
为自然对数的底数,则( )
A.若 为减函数,则 为减函数,则 | B.若 存在极值,则 存在极值,则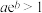 |
C.若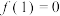 ,则 ,则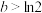 | D.若 ,则 ,则 |
您最近半年使用:0次



