广东省东莞市第七高级中学2023-2024学年高二下学期数学第一次月考数学试题
广东
高二
阶段练习
2024-04-12
256次
整体难度:
适中
考查范围:
函数与导数、计数原理与概率统计
一、单选题 添加题型下试题
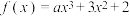 ,且
,且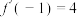 ,则实数a的值为( )
,则实数a的值为( )A.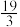 | B.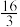 | C.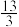 | D.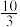 |
【知识点】 导数的乘除法 已知某点处的导数值求参数或自变量
| A.18 | B.24 | C.14 | D.16 |
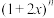 的展开式中所有项的系数和为243,则展开式中
的展开式中所有项的系数和为243,则展开式中 项的系数为( )
项的系数为( )| A.40 | B.60 | C.80 | D.160 |
【知识点】 求指定项的系数解读 二项展开式各项的系数和解读
4.  名同学从散打、跆拳道、击剑和太极拳四门课程中任选一门学习,则仅有跆拳道未被选中的概率为( )
名同学从散打、跆拳道、击剑和太极拳四门课程中任选一门学习,则仅有跆拳道未被选中的概率为( )
A.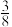 | B.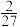 | C.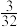 | D.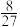 |
【知识点】 分步乘法计数原理及简单应用解读 计算古典概型问题的概率
 的图象大致为( )
的图象大致为( )A. | B.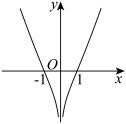 |
C.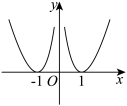 | D.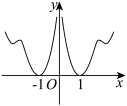 |
| A.152 | B.126 | C.90 | D.54 |
【知识点】 实际问题中的计数问题解读
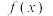 及其导函数
及其导函数 满足
满足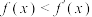 恒成立,且
恒成立,且 时
时 ,则下列式子不一定成立的是( )
,则下列式子不一定成立的是( )A. 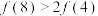 | B. 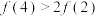 |
C. 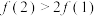 | D. 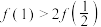 |
【知识点】 用导数判断或证明已知函数的单调性 比较函数值的大小关系
 时,
时,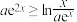 恒成立,则
恒成立,则 的取值范围为( )
的取值范围为( )A.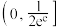 | B. |
C. | D.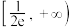 |
二、多选题 添加题型下试题
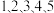 的五个球及四个不同的盒子,则下列表述正确的有( )
的五个球及四个不同的盒子,则下列表述正确的有( )A.全部投入4个不同的盒子里,允许有空盒,共有 种放法 种放法 |
B.全部投入4个不同的盒子里,没有空盒,共有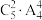 种不同的放法 种不同的放法 |
C.将其中的4个球投入4个盒子里的一个(另一个球不投入),共有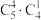 种放法 种放法 |
D.全部投入2个不同的盒子里,每盒至少一个,共有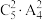 种放法 种放法 |
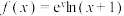 ,
, 是
是 的导数,则( )
的导数,则( )A.函数 在 在 上单调递增 上单调递增 |
B.函数 有唯一极小值 有唯一极小值 |
C.函数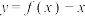 在 在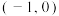 上有且只有一个零点 上有且只有一个零点 ,且 ,且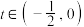 |
D.对于任意的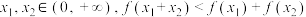 恒成立 恒成立 |
三、填空题 添加题型下试题
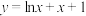 的一条切线的斜率为2,则该切线的方程为
的一条切线的斜率为2,则该切线的方程为【知识点】 求过一点的切线方程 已知切线(斜率)求参数
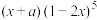 的展开式中
的展开式中 的系数为70,则实数
的系数为70,则实数
【知识点】 由项的系数确定参数解读 两个二项式乘积展开式的系数问题解读
四、解答题 添加题型下试题
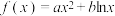 在
在 处有极值
处有极值 .
.(1)求
 、
、 的值;
的值;(2)求出
 的单调区间,并求极值.
的单调区间,并求极值.
 、
、 、
、 、
、 、
、 、
、 站成一排照相,求符合以下要求的站法.
站成一排照相,求符合以下要求的站法.(1)
 、
、 、
、 三位同学从左到右按照由高到矮的顺序站,共有多少种站法;
三位同学从左到右按照由高到矮的顺序站,共有多少种站法;(2)
 不在排头,
不在排头, 不在排尾,共有多少种站法.
不在排尾,共有多少种站法.
 系列进行市场销售量调研,通过对该品牌的
系列进行市场销售量调研,通过对该品牌的 系列一个阶段的调研得知,发现
系列一个阶段的调研得知,发现 系列每日的销售量
系列每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (元/千克)近似满足关系式
(元/千克)近似满足关系式 ,其中
,其中 ,
, 为常数.已知销售价格为6元/千克时,每日可售出
为常数.已知销售价格为6元/千克时,每日可售出 系列15千克.
系列15千克.(1)求函数
 的解析式;
的解析式;(2)若
 系列的成本为4元/千克,试确定销售价格
系列的成本为4元/千克,试确定销售价格 的值,使该商场每日销售
的值,使该商场每日销售 系列所获得的利润最大.
系列所获得的利润最大.
【知识点】 利用给定函数模型解决实际问题 利润最大问题
 ,
, 是正整数,
是正整数,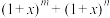 的展开式中
的展开式中 的系数为15.
的系数为15.(1)求展开式中
 的系数的最小值;
的系数的最小值;(2)已知
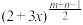 展开式中的二项式系数的最大值为
展开式中的二项式系数的最大值为 ,项的系数的最大值为
,项的系数的最大值为 ,求
,求 .
.
 .
.(1)讨论
 的单调性;
的单调性;(2)设
 ,
, 分别为
分别为 的极大值点和极小值点,记
的极大值点和极小值点,记 ,
,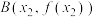 .
.(ⅰ)证明:直线AB与曲线
 交于另一点C;
交于另一点C;(ⅱ)在(i)的条件下,判断是否存在常数
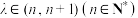 ,使得
,使得 .若存在,求n;若不存在,说明理由.
.若存在,求n;若不存在,说明理由.附:
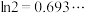 ,
,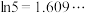 .
.
试卷分析
导出试卷题型(共 19题)
试卷难度
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 导数的乘除法 已知某点处的导数值求参数或自变量 | |
| 2 | 0.85 | 分步乘法计数原理及简单应用 元素(位置)有限制的排列问题 | |
| 3 | 0.85 | 求指定项的系数 二项展开式各项的系数和 | |
| 4 | 0.85 | 分步乘法计数原理及简单应用 计算古典概型问题的概率 | |
| 5 | 0.65 | 函数奇偶性的定义与判断 函数图像的识别 用导数判断或证明已知函数的单调性 | |
| 6 | 0.65 | 实际问题中的计数问题 | |
| 7 | 0.4 | 用导数判断或证明已知函数的单调性 比较函数值的大小关系 | |
| 8 | 0.4 | 函数单调性、极值与最值的综合应用 利用导数研究不等式恒成立问题 | |
| 二、多选题 | |||
| 9 | 0.85 | 导数的运算法则 简单复合函数的导数 | |
| 10 | 0.65 | 分步乘法计数原理及简单应用 实际问题中的组合计数问题 分组分配问题 | |
| 11 | 0.4 | 用导数判断或证明已知函数的单调性 利用导数研究不等式恒成立问题 利用导数研究函数的零点 | |
| 三、填空题 | |||
| 12 | 0.65 | 求过一点的切线方程 已知切线(斜率)求参数 | 单空题 |
| 13 | 0.85 | 由项的系数确定参数 两个二项式乘积展开式的系数问题 | 单空题 |
| 14 | 0.4 | 求过一点的切线方程 根据极值点求参数 | 单空题 |
| 四、解答题 | |||
| 15 | 0.85 | 利用导数求函数的单调区间(不含参) 求已知函数的极值 根据极值求参数 根据极值点求参数 | 问答题 |
| 16 | 0.85 | 全排列问题 元素(位置)有限制的排列问题 其他排列模型 | 问答题 |
| 17 | 0.94 | 利用给定函数模型解决实际问题 利润最大问题 | 应用题 |
| 18 | 0.65 | 二项式系数的增减性和最值 求指定项的系数 由项的系数确定参数 求系数最大(小)的项 | 问答题 |
| 19 | 0.15 | 用导数判断或证明已知函数的单调性 函数单调性、极值与最值的综合应用 | 证明题 |

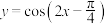 ,则
,则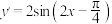
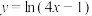 ,则
,则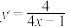
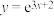 ,则
,则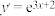
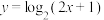 ,则
,则
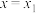 和
和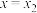 分别是函数
分别是函数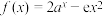 (
( 且
且 )的极小值点和极大值点.若
)的极小值点和极大值点.若 ,则a的取值范围是
,则a的取值范围是

