1 . 已知函数 ,当
,当 时,
时, 有极大值
有极大值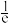 .
.
(1)求实数 的值;
的值;
(2)当 时,证明:
时,证明: .
.
 ,当
,当 时,
时, 有极大值
有极大值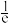 .
.(1)求实数
 的值;
的值;(2)当
 时,证明:
时,证明: .
.
您最近半年使用:0次
2024-03-04更新
|
2116次组卷
|
4卷引用:安徽省合肥市2024届高三第一次教学质量检查数学试题
名校
2 . 已知函数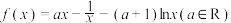 .
.
(1)当 时,求曲线
时,求曲线 在点
在点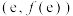 处的切线方程;
处的切线方程;
(2)若 既存在极大值,又存在极小值,求实数
既存在极大值,又存在极小值,求实数 的取值范围.
的取值范围.
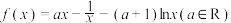 .
.(1)当
 时,求曲线
时,求曲线 在点
在点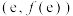 处的切线方程;
处的切线方程;(2)若
 既存在极大值,又存在极小值,求实数
既存在极大值,又存在极小值,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024-03-04更新
|
2533次组卷
|
5卷引用:广东省汕头市2024届高三第一次模拟考试数学试题
广东省汕头市2024届高三第一次模拟考试数学试题(已下线)第2套 重组模拟卷(模块二 2月开学)(已下线)宁夏石嘴山市平罗中学2024届高三下学期第一次模拟考试数学(文)试题四川省绵阳市三台中学校2024届高三下学期第二学月测试文科数学试题(已下线)第七套 艺体生新高考全真模拟 (一模重组卷)
名校
解题方法
3 . 已知函数 在
在 处取得极小值1,则
处取得极小值1,则 ( )
( )
 在
在 处取得极小值1,则
处取得极小值1,则 ( )
( )A. | B. |
C.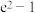 | D.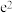 |
您最近半年使用:0次
2024-03-03更新
|
2195次组卷
|
12卷引用:江苏省泰州市2023-2024学年高二上学期1月期末数学试题
江苏省泰州市2023-2024学年高二上学期1月期末数学试题(已下线)模块一 专题3 导数在研究函数极值和最值中的应用(讲)(已下线)6.2.2 导数与函数的极值、最值(2知识点+6题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)广东省揭阳市惠来县第一中学2023-2024学年高二下学期3月月考数学试题广东省惠州市博罗县博罗中学2023-2024学年高二下学期3月月考数学试题广东省湛江市第二十一中学2023-2024学年高二下学期第一次月考数学试卷广东省东莞市塘厦中学2023-2024学年高二下学期4月月考数学试卷四川省眉山市仁寿县2023-2024学年高二下学期第一次教学质量监测(期中)数学试题(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》(苏教版)(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》A基础卷(苏教版)(已下线)模块一 专题5 导数在研究函数性质中的应用B提升卷(高二人教B版)(已下线)模块一 专题5 导数在研究函数性质中的应用(2)【高二下人教B版】
名校
4 . 函数 ,
,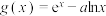 ,
, .已知
.已知 有极小值
有极小值 ,
, 有极小值
有极小值 .
.
(1)求 的取值范围;
的取值范围;
(2)若 ,求
,求 .
.
 ,
,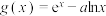 ,
, .已知
.已知 有极小值
有极小值 ,
, 有极小值
有极小值 .
.(1)求
 的取值范围;
的取值范围;(2)若
 ,求
,求 .
.
您最近半年使用:0次
名校
解题方法
5 . 已知函数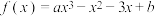 ,且当
,且当 时,
时, 有极值
有极值 .
.
(1)求 的解析式;
的解析式;
(2)求 在
在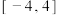 上的最大值和最小值.
上的最大值和最小值.
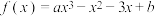 ,且当
,且当 时,
时, 有极值
有极值 .
.(1)求
 的解析式;
的解析式;(2)求
 在
在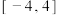 上的最大值和最小值.
上的最大值和最小值.
您最近半年使用:0次
2024-03-01更新
|
1368次组卷
|
8卷引用:安徽省淮南第一中学2023-2024学年高二下学期开学考试数学试题
安徽省淮南第一中学2023-2024学年高二下学期开学考试数学试题陕西省榆林市府谷县府谷中学2023-2024学年高二上学期开学考试数学试题(已下线)模块一 专题3 导数在研究函数极值和最值中的应用(讲)(已下线)第六章:导数章末重点题型复习(2)(已下线)6.2.2 导数与函数的极值、最值(2知识点+6题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)山东省菏泽市外国语学校2023-2024学年高二下学期第一次月考数学试卷(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》(苏教版)(已下线)模块一 专题5 导数在研究函数性质中的应用(2)【高二下人教B版】
名校
解题方法
6 . 已知函数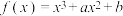 在
在 时取得极大值4,则
时取得极大值4,则
______ .
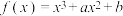 在
在 时取得极大值4,则
时取得极大值4,则
您最近半年使用:0次
2024-02-24更新
|
1297次组卷
|
12卷引用:陕西省西安市西安电子科技中学2023-2024学年高二上学期期末考试数学试题
陕西省西安市西安电子科技中学2023-2024学年高二上学期期末考试数学试题(已下线)模块一 专题3 导数在研究函数极值和最值中的应用(讲)(已下线)6.2.2 导数与函数的极值、最值(2知识点+6题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)广西壮族自治区百色市德保县德保高中2023-2024学年高二下学期3月月考数学试题甘肃省酒泉市实验中学2023-2024学年高二下学期3月月考数学试卷宁夏回族自治区石嘴山市平罗县平罗中学2023-2024学年高二下学期第一次月考(4月)数学试题黑龙江省绥化市哈尔滨师范大学青冈实验中学校2023-2024学年高二下学期4月月考数学试题(已下线)5.3.2.1函数的极值——随堂检测(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》(苏教版)广东省肇庆鼎湖中学2023-2024学年高二下学期4月段考数学试题(已下线)模块一 专题5 导数在研究函数性质中的应用(2)【高二下人教B版】(已下线)模块3 专题1 第4套 小题入门夯实练【高二人教B】
名校
解题方法
7 . 已知函数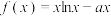 有极值
有极值 ,则
,则 ( )
( )
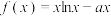 有极值
有极值 ,则
,则 ( )
( )| A.1 | B.2 | C. | D.3 |
您最近半年使用:0次
2024-02-23更新
|
1679次组卷
|
8卷引用:内蒙古自治区赤峰第四中学2023-2024学年高三下学期开学考试数学(理科)试题
8 . 已知函数 在
在 时取得极值 .
时取得极值 .
(1)求 的解析式;
的解析式;
(2)若函数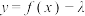 有一个零点,求实数
有一个零点,求实数 的取值范围.
的取值范围.
 在
在 时取得极值 .
时取得极值 .(1)求
 的解析式;
的解析式;(2)若函数
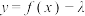 有一个零点,求实数
有一个零点,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024-02-22更新
|
518次组卷
|
2卷引用:【名校面对面】2022-2023学年高三大联考(1月)文数试题
9 . 若函数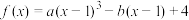 ,当
,当 时,函数
时,函数 有极值
有极值 .
.
(1)求函数 的解析式;
的解析式;
(2)若关于 的方程
的方程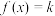 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
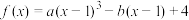 ,当
,当 时,函数
时,函数 有极值
有极值 .
.(1)求函数
 的解析式;
的解析式;(2)若关于
 的方程
的方程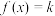 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024高二下·全国·专题练习
名校
解题方法
10 . 若函数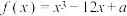 的极大值为11,则
的极大值为11,则 的极小值为
的极小值为____________ .
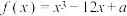 的极大值为11,则
的极大值为11,则 的极小值为
的极小值为
您最近半年使用:0次
2024-02-22更新
|
1575次组卷
|
9卷引用:5.3.2课时1函数的极值 第二练 强化考点训练
(已下线)5.3.2课时1函数的极值 第二练 强化考点训练(已下线)2.6.2函数的极值(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)第六章:导数章末重点题型复习(2)湖北省武汉市第三中学2023-2024学年高二下学期3月月考数学试题广东省佛山市第二中学2023-2024学年高二下学期第一次月考数学试题广东省惠州市博罗县博罗中学2023-2024学年高二下学期3月月考数学试题山东省济宁市微山县第二中学2023-2024学年高二下学期第一次月考数学试题广东省东莞市光明中学2023-2024学年高二下学期第一次月考数学试题四川省内江市第二中学2023-2024学年高二下学期第一次月考数学试题



