名校
1 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 有极小值,且极小值大于
有极小值,且极小值大于 ,求a的取值范围.
,求a的取值范围.
 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 有极小值,且极小值大于
有极小值,且极小值大于 ,求a的取值范围.
,求a的取值范围.
您最近一年使用:0次
2024-10-07更新
|
913次组卷
|
3卷引用:考点23 导数的应用--函数极值问题 --高考数学100个黄金考点(2025届)【讲】
(已下线)考点23 导数的应用--函数极值问题 --高考数学100个黄金考点(2025届)【讲】内蒙古包头市第六中学等多校联考2024-2025学年高三上学期开学考试数学试题云南省昆明市第九中学2025届高三上学期开学质量监测数学试题
2024高三·全国·专题练习
解题方法
2 . 已知函数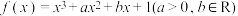 有极值,且导函数
有极值,且导函数 的极值点是
的极值点是 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明: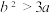 ;
;
(3)若 ,
, 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于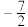 ,求a的取值范围.
,求a的取值范围.
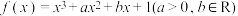 有极值,且导函数
有极值,且导函数 的极值点是
的极值点是 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b关于a的函数关系式,并写出定义域;
(2)证明:
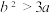 ;
;(3)若
 ,
, 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于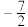 ,求a的取值范围.
,求a的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 若函数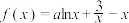 既有极大值也有极小值,则实数
既有极大值也有极小值,则实数 的取值范围为( )
的取值范围为( )
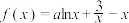 既有极大值也有极小值,则实数
既有极大值也有极小值,则实数 的取值范围为( )
的取值范围为( )A.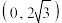 | B. |
C. | D.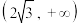 |
您最近一年使用:0次
2024-09-27更新
|
1253次组卷
|
5卷引用:第01节 函数与方程、不等式三者相互转化【讲】高三数学思想大全
(已下线)第01节 函数与方程、不等式三者相互转化【讲】高三数学思想大全(已下线)第05节 构造函数或构造方程解题的技巧【讲】高三数学思想大全河南省邓州市春雨国文学校2024-2025学年高三上学期10月月考数学试题吉林省东北师范大学附属中学2024-2025学年高三上学期第一次摸底考试数学试卷山东省新高考适应性考试2025届高三上学期10月质量检测数学试题
解题方法
4 . 已知函数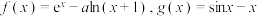 ,其中
,其中 .
.
(1)证明:当 时,
时,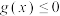 ;
;
(2)若 时,
时, 有极小值,求实数
有极小值,求实数 的取值范围;
的取值范围;
(3)对任意的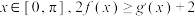 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
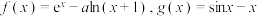 ,其中
,其中 .
.(1)证明:当
 时,
时,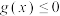 ;
;(2)若
 时,
时, 有极小值,求实数
有极小值,求实数 的取值范围;
的取值范围;(3)对任意的
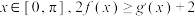 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-09-04更新
|
1200次组卷
|
3卷引用:导数中不等式恒成立问题
名校
解题方法
5 . 已知函数 在
在 时取得极值,且满足
时取得极值,且满足 .
.
(1)求函数 的解析式;
的解析式;
(2)若存在实数 ,使得
,使得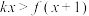 成立,求整数
成立,求整数 的最小值.
的最小值.
 在
在 时取得极值,且满足
时取得极值,且满足 .
.(1)求函数
 的解析式;
的解析式;(2)若存在实数
 ,使得
,使得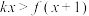 成立,求整数
成立,求整数 的最小值.
的最小值.
您最近一年使用:0次
2024-09-02更新
|
1341次组卷
|
4卷引用:考点24 导数的应用--函数最值问题 --高考数学100个黄金考点(2025届)【讲】
(已下线)考点24 导数的应用--函数最值问题 --高考数学100个黄金考点(2025届)【讲】四川省广安友实学校2025届高三上学期开学考试数学试题重庆市第一中学校2025届高三上学期开学考试数学试卷广东省茂名市华南师范大学附属茂名滨海学校2025届高三上学期10月月考数学试题
解题方法
6 . 已知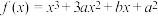 在
在 处有极值
处有极值 ,则
,则 ( )
( )
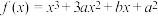 在
在 处有极值
处有极值 ,则
,则 ( )
( )A. 或 或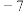 | B. 或 或 | C.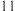 | D.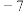 |
您最近一年使用:0次
解题方法
7 . 已知函数 .
.
(1)若函数 有极值,求实数
有极值,求实数 的取值范围;
的取值范围;
(2)若关于 的不等式
的不等式 在
在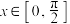 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 有极值,求实数
有极值,求实数 的取值范围;
的取值范围;(2)若关于
 的不等式
的不等式 在
在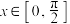 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
8 . 若函数 存在极大值,则实数
存在极大值,则实数 的取值范围为( )
的取值范围为( )
 存在极大值,则实数
存在极大值,则实数 的取值范围为( )
的取值范围为( )A. | B.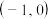 | C. | D.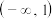 |
您最近一年使用:0次
2024-08-14更新
|
543次组卷
|
4卷引用:专题12 函数单调性 导数的符号(经典好题母题)【练】
(已下线)专题12 函数单调性 导数的符号(经典好题母题)【练】(已下线)考点23 导数的应用--函数极值问题 --高考数学100个黄金考点(2025届)【练】山东省威海市2023-2024学年高二下学期期末考试数学试题安徽省六安市毛坦厂中学2025届高三上学期9月月考数学试题
解题方法
9 . 已知函数 .
.
(1)若函数 在
在 处有极小值,求
处有极小值,求 的值;
的值;
(2)当 时,求证
时,求证 .
.
 .
.(1)若函数
 在
在 处有极小值,求
处有极小值,求 的值;
的值;(2)当
 时,求证
时,求证 .
.
您最近一年使用:0次
名校
解题方法
10 . 若函数 在
在 时有极小值
时有极小值 ,则
,则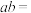 ( )
( )
 在
在 时有极小值
时有极小值 ,则
,则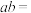 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次



