1 . 一个长为 ,宽为
,宽为 的长方形,取这个长方形的四条边的中点依次为
的长方形,取这个长方形的四条边的中点依次为 ,
, ,
, ,
, ,依次沿
,依次沿  ,
, ,
, ,
,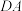 ,
,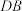 折叠,使得这个长方形的四个顶点都重合而得到的四面体,称为“萨默维尔四面体”,如下图,则这个四面体的体积为( )
折叠,使得这个长方形的四个顶点都重合而得到的四面体,称为“萨默维尔四面体”,如下图,则这个四面体的体积为( )
 ,宽为
,宽为 的长方形,取这个长方形的四条边的中点依次为
的长方形,取这个长方形的四条边的中点依次为 ,
, ,
, ,
, ,依次沿
,依次沿  ,
, ,
, ,
,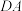 ,
,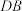 折叠,使得这个长方形的四个顶点都重合而得到的四面体,称为“萨默维尔四面体”,如下图,则这个四面体的体积为( )
折叠,使得这个长方形的四个顶点都重合而得到的四面体,称为“萨默维尔四面体”,如下图,则这个四面体的体积为( )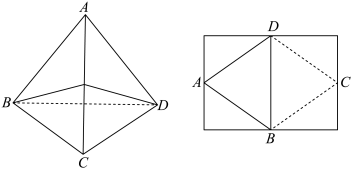
A. | B. | C. | D. |
您最近一年使用:0次
2024-07-15更新
|
236次组卷
|
2卷引用:北京市通州区2023-2024学年高一下学期期末数学试卷
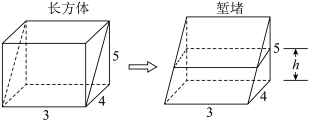
2 . “堑堵”最早的文字记载见于《九章算术》“商功”章.《九章算术·商功》刘徽注:“邪解立方得二堑堵,邪解堑堵,其一为阳马;其一为鳖臑.其中“堑堵”是一个长方体沿不在同一面上的相对两棱斜解所得的三棱柱,如图,长方体的长为3,宽为4,高为5,若堑堵中装满水,当水用掉一半时,水面的高为__________ .
您最近一年使用:0次
3 . 高一年级举办立体几何模型制作大赛,某同学想制作一个顶部是正四棱锥、底部是正四棱柱的模型,并画出了如图所示的直观图.其中正四棱柱.  的高
的高 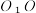 是正四棱锥.
是正四棱锥. 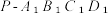 的高
的高 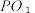 的4倍.
的4倍.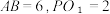 ;
;
(i)求该模型的体积;
(ii)求顶部正四棱锥的侧面积;
(2)若顶部正四棱锥的侧棱长为 6,当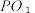 为多少时,底部正四棱柱的侧面积S最大?并求出S的最大值.
为多少时,底部正四棱柱的侧面积S最大?并求出S的最大值.
 的高
的高 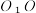 是正四棱锥.
是正四棱锥. 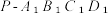 的高
的高 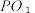 的4倍.
的4倍.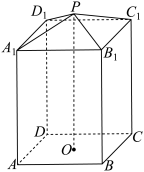
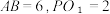 ;
;(i)求该模型的体积;
(ii)求顶部正四棱锥的侧面积;
(2)若顶部正四棱锥的侧棱长为 6,当
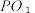 为多少时,底部正四棱柱的侧面积S最大?并求出S的最大值.
为多少时,底部正四棱柱的侧面积S最大?并求出S的最大值.
您最近一年使用:0次
2024-07-13更新
|
217次组卷
|
2卷引用:北京师范大学附属中学2023-2024学年高一下学期期末考试数学试题
23-24高二上·北京·期末
名校
解题方法
4 . 有下面两组几何体,根据要求填写所有符合条件的序号.
第①组:两个三棱锥分别是下图(左)中的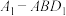 和下图(右)中的
和下图(右)中的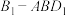 .
.

第②组:两个均由棱长为1的正方体组成的组合体.
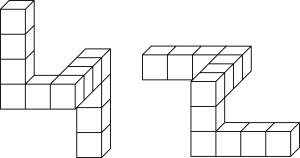
其中,第_________ 组中的两个几何体的体积相同,第_________ 组中的两个几何体不同.(两个几何体相同指的是它们可以通过整体平移或旋转后重合.)
第①组:两个三棱锥分别是下图(左)中的
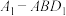 和下图(右)中的
和下图(右)中的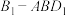 .
.
第②组:两个均由棱长为1的正方体组成的组合体.

其中,第
您最近一年使用:0次
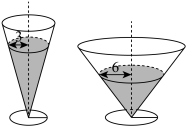
5 . 两个顶点朝下竖直放置的圆锥形容器盛有体积相同的同种液体(示意图如图所示),液体表面圆的半径分别为3,6,则窄口容器与宽口容器的液体高度的比值等于__________ .

您最近一年使用:0次
6 . 作为我国古代称量粮食的量器,米斗有着吉祥的寓意,是丰饶富足的象征,带有浓郁的民间文化韵味.右图是一件清代老木米斗,可以近似看作正四棱台,测量得其内高为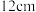 ,两个底面内棱长分别为
,两个底面内棱长分别为 和
和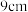 ,则估计该米斗的容积为
,则估计该米斗的容积为__________  .
.

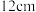 ,两个底面内棱长分别为
,两个底面内棱长分别为 和
和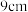 ,则估计该米斗的容积为
,则估计该米斗的容积为 .
.
您最近一年使用:0次
2024-02-10更新
|
550次组卷
|
2卷引用:北京市海淀区2023-2024学年高二上学期期末练习数学试卷
名校
解题方法
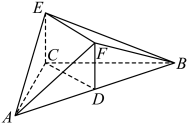
7 . 风筝又称为“纸鸢”,由中国古代劳动人民发明于距今2000多年的东周春秋时期,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.如图,是某高一年上级学生制作的一个风筝模型的多面体 为
为 的中点,四边形
的中点,四边形 为矩形,且
为矩形,且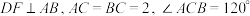 ,当
,当 时,多面体
时,多面体 的体积为( )
的体积为( )
 为
为 的中点,四边形
的中点,四边形 为矩形,且
为矩形,且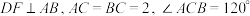 ,当
,当 时,多面体
时,多面体 的体积为( )
的体积为( )
A. | B. | C. | D. |
您最近一年使用:0次
2023-07-20更新
|
1043次组卷
|
7卷引用:北京市东城区第一六六中学2024届高三上学期期末模拟测试数学试题
北京市东城区第一六六中学2024届高三上学期期末模拟测试数学试题(已下线)北京市东城区第一六六中学2023-2024学年高三上学期期末模拟考试数学试题河北省张家口市2023届高三三模数学试题(已下线)专题10 空间向量与立体几何-2山西省运城市运城中学2023届高三第二次模拟数学试题(已下线)第01讲 空间几何体的结构特征、表面积与体积(练习)(已下线)8.6.2 直线与平面垂直(第1课时)直线与平面垂直的判定(导学案) -【上好课】
解题方法
8 . 已知正三棱锥 的六条棱长均为
的六条棱长均为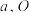 是底面
是底面 的中心,用一个平行于底面的平面截三棱锥,分别交
的中心,用一个平行于底面的平面截三棱锥,分别交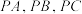 于
于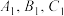 点(不与顶点
点(不与顶点 ,
, 重合).
重合).
给出下列四个结论:
①三棱锥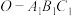 为正三棱锥;
为正三棱锥;
②三棱锥 的高为
的高为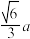 ;
;
③三棱锥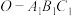 的体积既有最大值,又有最小值;
的体积既有最大值,又有最小值;
④当 时,
时,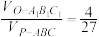 .
.
其中所有正确结论的序号是__________ .
 的六条棱长均为
的六条棱长均为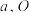 是底面
是底面 的中心,用一个平行于底面的平面截三棱锥,分别交
的中心,用一个平行于底面的平面截三棱锥,分别交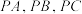 于
于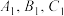 点(不与顶点
点(不与顶点 ,
, 重合).
重合).给出下列四个结论:
①三棱锥
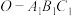 为正三棱锥;
为正三棱锥;②三棱锥
 的高为
的高为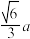 ;
;③三棱锥
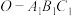 的体积既有最大值,又有最小值;
的体积既有最大值,又有最小值;④当
 时,
时,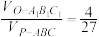 .
.其中所有正确结论的序号是
您最近一年使用:0次
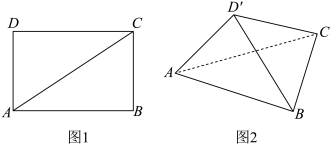
9 . 如图1,四边形 是矩形,将
是矩形,将 沿对角线
沿对角线 折起成
折起成 ,连接
,连接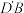 ,如图2,构成三棱锥
,如图2,构成三棱锥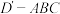 .过动点
.过动点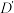 作平面
作平面 的垂线
的垂线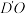 ,垂足是
,垂足是 .
. 落在何处时,平面
落在何处时,平面 平面
平面 ,并说明理由;
,并说明理由;
(2)在三棱锥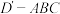 中,若
中,若 为
为 的中点,判断直线
的中点,判断直线 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)设 是
是 及其内部的点构成的集合,
及其内部的点构成的集合, ,当
,当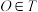 时,求三棱锥
时,求三棱锥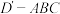 的体积的取值范围.
的体积的取值范围.
 是矩形,将
是矩形,将 沿对角线
沿对角线 折起成
折起成 ,连接
,连接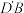 ,如图2,构成三棱锥
,如图2,构成三棱锥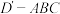 .过动点
.过动点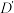 作平面
作平面 的垂线
的垂线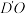 ,垂足是
,垂足是 .
.
 落在何处时,平面
落在何处时,平面 平面
平面 ,并说明理由;
,并说明理由;(2)在三棱锥
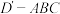 中,若
中,若 为
为 的中点,判断直线
的中点,判断直线 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(3)设
 是
是 及其内部的点构成的集合,
及其内部的点构成的集合, ,当
,当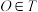 时,求三棱锥
时,求三棱锥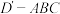 的体积的取值范围.
的体积的取值范围.
您最近一年使用:0次
2022-07-11更新
|
488次组卷
|
6卷引用:北京市大兴区2021-2022学年高一下学期期末检测数学试题
北京市大兴区2021-2022学年高一下学期期末检测数学试题黑龙江省鹤岗市宝泉岭高级中学2023-2024学年高一下学期7月期末数学试题河北省赵县中学2022-2023学年高一下学期5月月考数学试题河北省石家庄市五校联合体2022-2023学年高一下学期期中数学试题(已下线)模块五 高一下期中重组篇(河北)(已下线)专题06 空间中点线面的位置关系6种常考题型归类(2) -期期末真题分类汇编(北京专用)
10 . 已知一个圆柱与一个圆锥的底面半径相等,圆柱的高等于其底面直径,圆锥的高等于其底面直径的 倍.给出下列结论:
倍.给出下列结论:
①设圆柱与圆锥的体积分别为 、
、 ,则
,则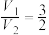 ;
;
②设圆柱与圆锥的轴截面面积分别为 、
、 ,则
,则 ;
;
③设圆柱与圆锥的侧面积分别为 、
、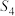 ,则
,则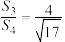 ;
;
④设圆柱与圆锥表面积分别为 、
、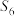 ,则
,则 .
.
其中所有正确结论的序号是( )
 倍.给出下列结论:
倍.给出下列结论:①设圆柱与圆锥的体积分别为
 、
、 ,则
,则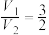 ;
;②设圆柱与圆锥的轴截面面积分别为
 、
、 ,则
,则 ;
;③设圆柱与圆锥的侧面积分别为
 、
、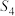 ,则
,则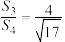 ;
;④设圆柱与圆锥表面积分别为
 、
、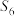 ,则
,则 .
.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①③④ | D.①②③④ |
您最近一年使用:0次



