1 . 如图,在底面是菱形的四棱锥 中,
中, 为
为 中点,
中点,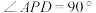 ,
,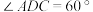 ,已知
,已知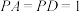 .
.
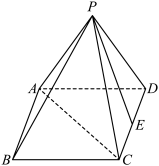
(1)若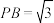 ,证明:
,证明: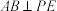 ;
;
(2)若 ,求二面角
,求二面角 的平面角的正弦值.
的平面角的正弦值.
 中,
中, 为
为 中点,
中点,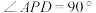 ,
,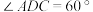 ,已知
,已知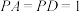 .
.
(1)若
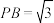 ,证明:
,证明: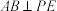 ;
;(2)若
 ,求二面角
,求二面角 的平面角的正弦值.
的平面角的正弦值.
您最近一年使用:0次
名校
解题方法
2 . 如图,在多面体 中,平面
中,平面 平面
平面 ,
, ,
, ,
,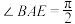 ,
,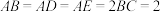 ,
, 是
是 的中点.
的中点.
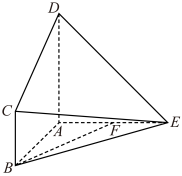
(1)证明: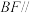 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
,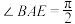 ,
,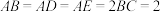 ,
, 是
是 的中点.
的中点.
(1)证明:
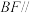 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2022-12-17更新
|
750次组卷
|
7卷引用:江苏省淮安市洪泽湖高级中学2022-2023学年高二下学期第一次月考数学试题
3 . 如图,在三棱柱 中,侧面
中,侧面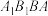 和侧面
和侧面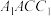 均为正方形,
均为正方形, 为棱
为棱 的中点.
的中点.
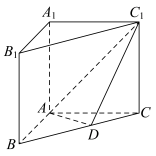
(1)证明:平面 平面
平面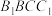 ;
;
(2)若直线 与平面
与平面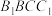 所成角为30°,求平面
所成角为30°,求平面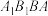 与平面
与平面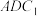 夹角的余弦值.
夹角的余弦值.
 中,侧面
中,侧面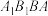 和侧面
和侧面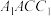 均为正方形,
均为正方形, 为棱
为棱 的中点.
的中点.
(1)证明:平面
 平面
平面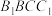 ;
;(2)若直线
 与平面
与平面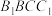 所成角为30°,求平面
所成角为30°,求平面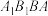 与平面
与平面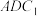 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2023-03-10更新
|
1771次组卷
|
5卷引用:江苏省淮安市涟水县第一中学2022-2023学年高二下学期第一次月考数学试题
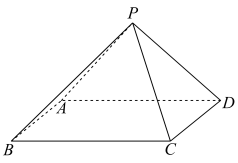
4 . 已知四棱锥 的底面为正方形,侧面PAD为等腰直角三角形,
的底面为正方形,侧面PAD为等腰直角三角形, ,平面
,平面 平面ABCD,平面
平面ABCD,平面 平面
平面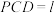 .
.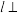 平面PAD;
平面PAD;
(2)设M为l上一点,求PC与平面MAD所成角正弦值的最小值.
 的底面为正方形,侧面PAD为等腰直角三角形,
的底面为正方形,侧面PAD为等腰直角三角形, ,平面
,平面 平面ABCD,平面
平面ABCD,平面 平面
平面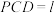 .
.
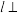 平面PAD;
平面PAD;(2)设M为l上一点,求PC与平面MAD所成角正弦值的最小值.
您最近一年使用:0次
2022-07-08更新
|
786次组卷
|
5卷引用:江苏省淮安市2021-2022学年高二下学期期末数学试题
名校
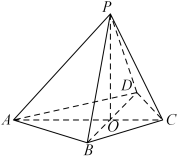
5 . 如图,在四棱锥 中,
中, 和
和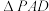 均为正三角形,且边长为
均为正三角形,且边长为 ,
, ,
, ,
, 与
与 交于点
交于点 .
. 平面
平面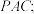
(2)求二面角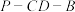 的余弦值.
的余弦值.
 中,
中, 和
和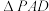 均为正三角形,且边长为
均为正三角形,且边长为 ,
, ,
, ,
, 与
与 交于点
交于点 .
.
 平面
平面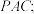
(2)求二面角
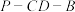 的余弦值.
的余弦值.
您最近一年使用:0次
2022-07-02更新
|
463次组卷
|
4卷引用:江苏省淮安市马坝高级中学2022-2023学年高三上学期第一次检测数学试题
名校
解题方法
6 . 在矩形ABCD中,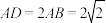 ,点E是线段AD的中点,将△ABE沿BE折起到△PBE位置(如图),点F是线段CP的中点.
,点E是线段AD的中点,将△ABE沿BE折起到△PBE位置(如图),点F是线段CP的中点.
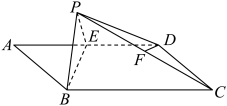
(1)求证:DF∥平面PBE:
(2)若二面角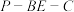 的大小为
的大小为 ,求点A到平面PCD的距离.
,求点A到平面PCD的距离.
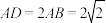 ,点E是线段AD的中点,将△ABE沿BE折起到△PBE位置(如图),点F是线段CP的中点.
,点E是线段AD的中点,将△ABE沿BE折起到△PBE位置(如图),点F是线段CP的中点.
(1)求证:DF∥平面PBE:
(2)若二面角
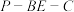 的大小为
的大小为 ,求点A到平面PCD的距离.
,求点A到平面PCD的距离.
您最近一年使用:0次
2022-05-27更新
|
1313次组卷
|
7卷引用:江苏省淮安市2022届高三下学期5月模拟数学试题
名校
解题方法
7 . 如图, 为圆柱
为圆柱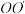 的轴截面,
的轴截面, 是圆柱上异于
是圆柱上异于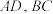 的母线.
的母线.
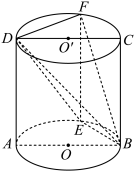
(1)证明: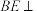 平面
平面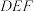 ;
;
(2)若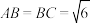 ,当三棱锥
,当三棱锥 的体积最大时,求二面角
的体积最大时,求二面角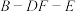 的正弦值.
的正弦值.
 为圆柱
为圆柱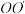 的轴截面,
的轴截面, 是圆柱上异于
是圆柱上异于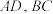 的母线.
的母线.
(1)证明:
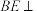 平面
平面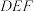 ;
;(2)若
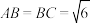 ,当三棱锥
,当三棱锥 的体积最大时,求二面角
的体积最大时,求二面角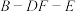 的正弦值.
的正弦值.
您最近一年使用:0次
2022-07-06更新
|
2142次组卷
|
21卷引用:江苏省金湖、洪泽等四校联盟2021-2022学年高一下学期第三次学情调查数学试题
江苏省金湖、洪泽等四校联盟2021-2022学年高一下学期第三次学情调查数学试题广东省2022届高三一模数学试题山东省济南市实验中学2021-2022学年高一下学期04月月考数学试题湖南省株洲市第二中学2021-2022学年高二下学期期中数学试题江苏省华罗庚中学等三校2021-2022学年高三下学期4月联合调研数学试题河北省"五个一"名校联盟2023届高三上学期摸底数学试题(已下线)专题32 空间向量及其应用-5(已下线)专题24 立体几何解答题最全归纳总结-1(已下线)专题21 利用传统方法求线线角、线面角、二面角与距离的问题-1(已下线)专题5 综合闯关(提升版)广东省广州市第十七中学2022-2023学年高一上学期期中数学试题陕西省西安中学2022届高三下学期考前适应性考试理科数学试题浙江省杭州学军中学2022-2023学年高二上学期期中数学试题(已下线)广东省2022届高三一模数学试题变式题17-22(已下线)专题19 空间几何解答题(理科)-1陕西省咸阳市武功县普集高级中学2023届高三下学期五模理科数学试题广东省东莞实验中学2023届高三一模数学试题湖北省恩施州高中教育联盟2022-2023学年高二下学期期中数学试题(已下线)广东省佛山市南海区桂城中学2024届高三上学期10月月考数学试题贵州省黔西南州金成实验学校2023-2024学年高二上学期期中考试数学试题湖南省永州市祁阳县第四中学2023-2024学年高二上学期期中数学试题
8 . 如图,四面体 中,
中,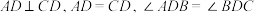 ,E为
,E为 的中点.
的中点.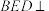 平面
平面 ;
;
(2)设 ,点F在
,点F在 上,当
上,当 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 中,
中,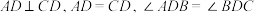 ,E为
,E为 的中点.
的中点.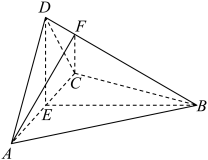
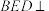 平面
平面 ;
;(2)设
 ,点F在
,点F在 上,当
上,当 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
您最近一年使用:0次
2022-06-07更新
|
49855次组卷
|
51卷引用:江苏省淮安市盱眙中学2023届高三下学期模拟训练八数学试题
江苏省淮安市盱眙中学2023届高三下学期模拟训练八数学试题2022年高考全国乙卷数学(理)真题(已下线)2022年全国高考乙卷数学(理)试题变式题9-12题(已下线)第6讲 立体几何(已下线)专题40:空间角的向量求法-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题17 立体几何解答题(已下线)专题32 空间向量及其应用-4(已下线)第06讲 向量法求空间角(含探索性问题) (讲)-3(已下线)7.5 空间向量求空间角(精练)(已下线)2022年全国高考乙卷数学(理)试题变式题17-20题(已下线)第52讲 空间向量在立体几何中的运用(已下线)第04讲 空间向量在立体几何中的应用(练,理科专用)浙江省绍兴市柯桥中学2022-2023学年高二上学期10月月考数学试题(已下线)考向28利用空间向量求空间角(重点)湖北省随州市曾都区第一中学2022-2023学年高二上学期期中模拟数学试题(已下线)专题08 立体几何解答题常考全归类(精讲精练)-1(已下线)专题6 第3讲 立体几何中的向量方法湖南省岳阳县第一中学、汨罗市第一中学2022-2023学年高二上学期期末考试数学试题湖南省长郡中学2023届高三下学期月考(七)数学试题(已下线)大题强化训练(9)(已下线)模块三 专题7 立体几何(已下线)专题14 押全国卷(理科)第18题 立体几何(已下线)第4讲 空间向量的应用 (2)(已下线)专题19 空间几何解答题(理科)-3全国甲乙卷3年真题分类汇编《立体几何》解答题全国甲乙卷5年真题分类汇编《立体几何》解答题(已下线)专题10 空间向量与立体几何-1内蒙古自治区巴彦淖尔市衡越实验中学2022-2023学年高二下学期期中数学(理)试题1.4空间向量的应用(已下线)模块一 情境7 以立体几何为背景(已下线)第11讲 用空间向量研究距离、夹角问题11种常见考法归类-【暑假自学课】2023年新高二数学暑假精品课(人教A版2019选择性必修第一册)江苏省扬州市仪征中学2022-2023学年高三下学期3月学情测试数学试题福建省厦门第一中学2023届高三二模数学试题(已下线)第三章 空间向量与立体几何(综合提升检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)四川省资阳市乐至县乐至中学2023-2024学年高二上学期10月月考数学试题(已下线)1.4.2 用空间向量研究距离、夹角问题【第三课】安徽省淮北市树人高级中学2023-2024学年高二上学期第一次阶段考试数学试题河南省信阳市固始县高级中学第一中学2023-2024学年高二上学期第一次月考数学试题湖南省邵阳市新邵县第三中学2023-2024学年高二上学期期中数学试题(已下线)模块六 立体几何 大招16 叉乘法快速求法向量(已下线)第5讲:立体几何中的动态问题【练】(已下线)专题05 空间向量与立体几何(分层练)(四大题型+21道精选真题)(已下线)第4讲:立体几何中的最值问题【练】(清北二轮)(已下线)专题06 立体几何 第一讲 立体几何中的证明问题(解密讲义)(已下线)专题06 立体几何 第一讲 立体几何中的证明问题(分层练)(已下线)专题23 立体几何解答题(理科)-1(已下线)【一题多变】空间最值 向量求解专题07立体几何与空间向量专题30立体几何与空间向量解答题(第一部分)(已下线)三年全国理科专题08立体几何与空间向量(已下线)五年全国理科专题16立体几何与空间向量解答题
名校
9 . 如图1所示,梯形ABCD中,AD=2AB=2BC=2CD=4.E为AD的中点,连结BE,AC交于F,将△ABE沿BE折叠,使得平面ABE⊥平面BCDE(如图2)

(1)求证:AF⊥CD;
(2)求平面AFC与平面ADE所成的二面角的正弦值.

(1)求证:AF⊥CD;
(2)求平面AFC与平面ADE所成的二面角的正弦值.
您最近一年使用:0次
2022-03-16更新
|
732次组卷
|
5卷引用:江苏省淮安市2021届高三下学期4月第二次适应性考试数学试题
江苏省淮安市2021届高三下学期4月第二次适应性考试数学试题西藏林芝市、日喀则市2021届高三下学期第二次联考数学(理)试题江苏省泰州市泰兴市第一高级中学2022届高三下学期阶段测试二数学试题(已下线)查补易混易错点05 空间向量与立体几何-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)福建省莆田第二十五中学2021-2022学年高二下学期期中考试数学试题
解题方法
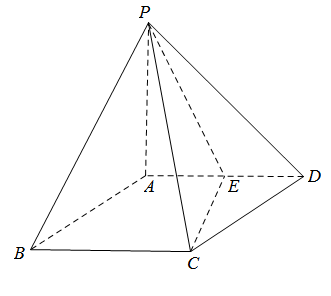
10 . 四棱锥 中,
中, 平面
平面 ,四边形
,四边形 为菱形,
为菱形,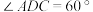 ,
,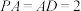 ,
, 为
为 的中点.
的中点.
(1)求证:平面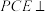 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求二面角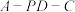 的余弦值.
的余弦值.
 中,
中, 平面
平面 ,四边形
,四边形 为菱形,
为菱形,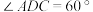 ,
,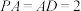 ,
, 为
为 的中点.
的中点.
(1)求证:平面
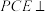 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求二面角
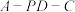 的余弦值.
的余弦值.
您最近一年使用:0次



