名校
1 . 下表是离散型随机变量 的分布列,则常数
的分布列,则常数 的值是( )
的值是( )
 的分布列,则常数
的分布列,则常数 的值是( )
的值是( )X | 3 | 4 | 5 | 9 |
P |
|
|
|
|
A. | B. | C.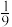 | D. |
您最近一年使用:0次
2023-09-07更新
|
1230次组卷
|
35卷引用:重庆市2018-2019学年高二5月数学(理)试题
重庆市2018-2019学年高二5月数学(理)试题(已下线)专题10.5 离散型随机变量及其分布列(讲)-浙江版《2020年高考一轮复习讲练测》山东省滨州市2018-2019学年高二下学期期中数学试题贵州省兴仁市凤凰中学2019-2020学年高二下学期第一次月考数学(理)试题广西钦州市第一中学2019-2020学年高二下学期期中考试数学(理)试题江苏省南京市临江高级中学2019-2020学年高二下学期期中数学试题江苏省常州市新桥高级中学2019-2020学年高二下学期期中数学试题(已下线)考点52 离散型随机变量及其分布列-备战2021年新高考数学一轮复习考点一遍过(已下线)4.2.2 离散型随机变量的分布列-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)广东省深圳实验学校高中部2023-2024学年高二下学期第一阶段考试数学试题(已下线)专题31 离散型随机变量及其分布列-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)专题4.2 随机变量与离散型随机变量的分布列(A卷基础篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)人教B版(2019) 选修第二册 名师精选 第四章 概率与 统计人教B版(2019) 选修第二册 过关检测 第四章 综合把关练人教A版(2019) 选修第三册 名师精选 第七章 随机变量及其分布 B卷(已下线)4.2.2离散型随机变量的分布列-2021-2022学年高二数学同步知识梳理+考点精讲精练(人教B版2019选择性必修第二册)山西省晋中市祁县中学2021-2022学年高二下学期4月月考数学(A)试题江苏省常州市第一中学、泰兴中学2021-2022学年高二下学期期中联考数学试题(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精练)(已下线)第07讲 离散型随机变量及其分布列和数字特征 (高频考点,精讲)山西省晋中市介休市第一中学校2022-2023学年高二下学期3月月考数学试题(已下线)7.2 离散型随机变量及其分布列(分层作业)湖北省仙桃市田家炳实验高级中学2022-2023学年高二下学期期中数学试题河北省石家庄市辛集市育才中学2022-2023学年高二下学期4月月考数学试题辽宁省朝阳市建平县实验中学2022-2023学年高二下学期3月月考数学试题(已下线)第五节 离散型随机变量及其分布列 A卷素养养成卷 一轮复习点点通(已下线)专题10 离散型随机变量及其分布列(六大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第09讲 离散型随机变量及其分布列-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)4.2.2 离散型随机变量的分布列(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)第10讲 第七章随机变量及其分布章节验收测评卷-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.2 离散型随机变量及其分布列——课后作业(提升版)(已下线)第7.2讲 离散型随机变量及其分布列-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选择性必修第三册)(已下线)7.2 离散型随机变量及其分布列(5大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)天津市滨海新区田家炳中学2023-2024学年高二上学期期中考试数学试题广西钦州市2023-2024学年高二下学期期中考试数学试卷
名校
2 . 甲、乙两人下象棋,赢了得3分,平局得1分,输了得0分,共下三局.用ξ表示甲的得分,则{ξ=3}表示( )
| A.甲赢三局 |
| B.甲赢一局 |
| C.甲、乙平局三次 |
| D.甲赢一局输两局或甲、乙平局三次 |
您最近一年使用:0次
2023-09-02更新
|
751次组卷
|
35卷引用:2018-2019学年北师大版高中数学选修2-3同步配套(课件+练习):2.1.1
2018-2019学年北师大版高中数学选修2-3同步配套(课件+练习):2.1.1人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 4.2.1 随机变量及其与事件的联系(已下线)4.2.1 随机变量及其与事件的关系-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)广东省江门市新会陈经纶中学2022-2023学年高二下学期期中数学试题(已下线)7.2 离散型随机变量及分布列(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.1随机变量及其与事件的联系B提高练(已下线)专题7.2离散型随机变量及其分布列(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)【新教材精创】7.2 离散型随机变量及其分布列 (1) -A基础练福建省三明第一中学2020-2021学年高二下学期期中数学试题江苏省扬州中学2020-2021学年高二下学期期中数学试题河北省石家庄市十九中2020-2021学年高二下学期第一次月考数学试题人教B版(2019) 选修第二册 突围者 第四章 第二节课时1 随机变量及其与事件的联系(已下线)第四章 概率与统计 4.2 随机变量 4.2.1 随机变量及其与事件的联系苏教版(2019) 选修第二册 限时训练 第23练 随机变量及其分布列(1)苏教版(2019) 选修第二册 名师精选 第八章 第六单元 随机变量及其分布列离散型随机变量的数字特征人教A版(2019) 选修第三册 名师精选 第四单元 离散型随机变量及其分布列、离散型随机变量的数字特征人教A版(2019) 选修第三册 实战演练 第七章 7.2 课时练习10 离散型随机变量及其分布列人教A版(2019) 选修第三册 过关斩将 第七章 7.2 离散型随机变量及其分布列(已下线)专题47:离散型随机变量的分布列-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题48 离散型随机变量的分布列与数字特征-1(已下线)考向41 离散型随机变量的分布列与数字特征(六大经典题型)-1(已下线)8.2.1随机变量及其分布列(1)云南省昭通市绥江县第一中学2020-2021学年高一下学期期末考试数学试题北师大版(2019) 选修第一册 数学奇书 学业评价(三十九) 随机变量(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)专题10 离散型随机变量及其分布列(六大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)第09讲 离散型随机变量及其分布列-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)6.2.1随机变量(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(理科)试题(二十一)(已下线)7.2离散型随机变量及其分布列 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)7.2 离散型随机变量及其分布列(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)7.2离散型随机变量及其分布列 第一练 练好课本试题(已下线)第7.2讲 离散型随机变量及其分布列-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选择性必修第三册)安徽省蚌埠市蚌埠铁路中学2023-2024学年高二下学期期中检测数学试题【课后练 】 3.2.1 离散型随机变量及其分布 课后作业-湘教版(2019)选择性必修第二册 第3章 概率
名校
3 . 已知离散型随机变量 的概率分布列如下表:则数学期望
的概率分布列如下表:则数学期望 等于( )
等于( )
 的概率分布列如下表:则数学期望
的概率分布列如下表:则数学期望 等于( )
等于( )
|
|
|
|
|
|
|
|
A. | B.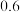 | C.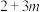 | D.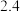 |
您最近一年使用:0次
2024-01-02更新
|
1208次组卷
|
19卷引用:广东省梅州市梅县区富力足球学校2019-2020学年高二下学期线上教学检测数学试题
广东省梅州市梅县区富力足球学校2019-2020学年高二下学期线上教学检测数学试题高中数学人教A版选修2-3 第二章 随机变量及其分布 本章复习与测试黑龙江省海林市朝鲜族中学人教版高中数学选修2-3同步练习:滚动习题(四)[范围2.1~2.4]黑龙江省鹤岗市工农区第一中学2019-2020学年高二上学期期末数学(理)试题广东省广东实验中学越秀学校2023-2024学年高二下学期5月段考数学试卷海南省琼海市嘉积第二中学2021-2022学年高二下学期教学质量监测(期末)数学试题江苏省淮安市马坝高级中学2022-2023学年高二下学期期中数学试题(已下线)专题11 离散型随机变量的数字特征(六大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(4)(已下线)第七章 随机变量及其分布(单元重点综合测试)(19题新结构)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(1)(已下线)7.3离散型随机变量的数字特征 第一课 解透课本内容(已下线)7.3.1 离散型随机变量的均值——随堂检测福建省厦门市湖滨中学2023-2024学年高二下学期期中考试数学试题天津北京师范大学静海附属学校 (天津市静海区北师大实验学校)2023-2024学年高二下学期第二次阶段检测(期中)数学试题(已下线)专题04随机变量及其分布(6大考点经典基础练+优选提升练)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(新高考专用)(已下线)核心考点6 离散型随机变量与分布列 B提升卷 (高二期末考试必考的10大核心考点)(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点1 随机变量的分布列、期望【基础版】
名校
4 . 一个口袋里装有大小相同的5个小球,其中红色有2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是_____ ;若变量X为取出的三个小球中红球的个数,则X的均值E(X)=_____ .
您最近一年使用:0次
2023-07-02更新
|
506次组卷
|
10卷引用:【校级联考】浙江省金华十校2019届高三上学期期末联考数学试题
【校级联考】浙江省金华十校2019届高三上学期期末联考数学试题(已下线)专题10.7 离散型随机变量的均值与方差(练)-浙江版《2020年高考一轮复习讲练测》(已下线)专题11.6 离散型随机变量的均值与方差(精练)-2021年新高考数学一轮复习学与练(已下线)专题11.6 离散型随机变量的均值与方差(练)-2021年新高考数学一轮复习讲练测广东省深圳市宝安区2023届高三上学期第一次调研(10月)数学试题天津市七校2020-2021学年高三上学期期末联考数学试题湖北省孝感高级中学2021届高三下学期2月调研考试数学试题天津市咸水沽第一中学2023届高考押题卷(二)数学试题6.4.2超几何分布 同步练习(已下线)7.4.2超几何分布 第二练 强化考点训练
名校
解题方法
5 . 随机变量X的分布列如表所示,若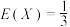 ,则
,则
_________ .
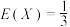 ,则
,则
| X | -1 | 0 | 1 |
| P |  | a | b |
您最近一年使用:0次
2023-01-30更新
|
1958次组卷
|
25卷引用:沪教版(2020) 一轮复习 堂堂清 第九单元 综合练习
沪教版(2020) 一轮复习 堂堂清 第九单元 综合练习广东省佛山市南海区石门中学2022-2023学年高二下学期第二次质量检测数学试题广东省肇庆市肇庆鼎湖中学2022-2023学年高二下学期6月月考数学试题江西省抚州市崇仁一中、广昌一中、金溪一中2022-2023学年高二下学期第一次月考数学试题(已下线)7.3 离散型随机变量的数字特征(练习)(已下线)8.2.2 离散型随机变量的数字特征(练习)广西钦州市第一中学2022-2023学年高二下学期期中考试数学试题(已下线)8.2.2离散型随机变量的数字特征-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)第7章 概率初步(续)(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020选择性必修第二册)安徽省阜阳市太和第一中学2022-2023学年高二下学期期中适应性考试数学试卷(已下线)模块四 专题4 期末重组综合练(广东)浙江省宁波赫威斯肯特学校2022-2023学年高二普高部下学期第一次月考数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(1)江西省上高二中2022-2023学年高二下学期2月月考数学试题黑龙江省鹤岗市第一中学2022-2023学年高二上学期期末数学试题(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)艺体生一轮复习 第九章 计数原理、概率与统计 第47讲 离散型随机变量的均值与方差【练】(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)第七章 概率初步(续)(知识归纳+题型突破)(2)(已下线)12.2 离散型随机变量及其分布列课前·考点引领基础再现宁夏石嘴山市第三中学2023-2024学年高一下学期第一次月考数学试卷宁夏石嘴山市第三中学2023-2024学年高二下学期第一次月考数学试卷(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)(已下线)7.3.2 离散型随机变量的方差——课后作业(提升版)(已下线)7.3 离散型随机变量的数字特征(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
20-21高二下·浙江·课后作业
名校
6 . 已知随机变量X的分布列如表(其中a为常数):
则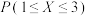 等于( )
等于( )
X | 0 | 1 | 2 | 3 | 4 | 5 |
P | 0.1 | 0.1 | a | 0.3 | 0.2 | 0.1 |
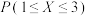 等于( )
等于( )| A.0.4 | B.0.5 | C.0.6 | D.0.7 |
您最近一年使用:0次
2022-09-03更新
|
2871次组卷
|
28卷引用:广东省台山市华侨中学2020-2021学年高二上学期第一次月考数学试题
广东省台山市华侨中学2020-2021学年高二上学期第一次月考数学试题(已下线)4.2.2 离散型随机变量的分布列-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)(已下线)专题7.2离散型随机变量及其分布列(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)4.2.2离散型随机变量的分布列A基础练(已下线)“8+4+4”小题强化训练(63)离散型随机变量及其分布列-2022届高考数学一轮复习(江苏等新高考地区专用)人教B版(2019) 选修第二册 过关检测 第四章 第4.2节 综合把关练苏教版(2019) 选修第二册 限时训练 第23练 随机变量及其分布列(1)人教A版(2019) 选修第三册 实战演练 第七章 7.2 课时练习10 离散型随机变量及其分布列人教A版(2019) 选修第三册 过关斩将 第七章 7.2 离散型随机变量及其分布列江苏省苏州市吴县中学2021-2022学年高二下学期期中数学试题北京市顺义牛栏山第一中学2021-2022学年高二下学期期中数学试题西藏林芝市第二高级中学2021-2022学年高二下学期第二学段考试(期末)数学(理)试题2023版 湘教版(2019) 选修第二册 过关斩将 第3章 3.2.1离散型随机变量及其分布四川省仁寿县文宫中学2022-2023学年高三9月月考数学(理)试题(已下线)专题48 离散型随机变量的分布列与数字特征-3(已下线)专题21 概率与成对数据的统计分析(讲义)-2(已下线)第07讲 离散型随机变量及其分布列和数字特征 (高频考点,精练)(已下线)离散型随机变量及其分布列(已下线)第四章 概率与统计(A卷·知识通关练)(2)(已下线)第七章 随机变量及其分布(A卷·知识通关练)(2)(已下线)第七章 随机变量及其分布 讲核心 01(已下线)第七章 随机变量及其分布 讲核心 02贵州省遵义清华中学2022-2023学年高二下学期第一次月考数学试题(已下线)第07讲 离散型随机变量的分布列及其性质4种常考题型吉林省普通高中友好学校第三十六届联合体2022-2023学年高二下学期期中联考数学试题山西省运城市景胜中学2022-2023学年高二下学期4月月考数学(B)试题新疆阿克苏市实验中学2022-2023学年高二下学期第二次月考数学试题(已下线)7.2 离散型随机变量及其分布列——随堂检测
名校
解题方法
7 . 有歌唱道:“江西是个好地方,山清水秀好风光.”现有甲、乙两位游客慕名来到江西旅游,准备从庐山、三清山、龙虎山和明月山四个著名旅游景点中随机选择一个景点游玩,记事件 为“甲和乙至少一人选择庐山”,事件
为“甲和乙至少一人选择庐山”,事件 为“甲和乙选择的景点不同”,则
为“甲和乙选择的景点不同”,则 ( )
( )
 为“甲和乙至少一人选择庐山”,事件
为“甲和乙至少一人选择庐山”,事件 为“甲和乙选择的景点不同”,则
为“甲和乙选择的景点不同”,则 ( )
( )A. | B.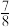 | C.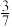 | D.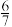 |
您最近一年使用:0次
2022-11-30更新
|
1239次组卷
|
23卷引用:江西省重点中学协作体2020届高三第一次联考数学(理科)试题
江西省重点中学协作体2020届高三第一次联考数学(理科)试题福建省三明第一中学2019-2020学年高二下学期阶段2考试数学试题(已下线)第47练 随机变量及其分布-2021年高考数学(理)一轮复习小题必刷江西省余干县新时代学校2020-2021学年高二上学期阶段测试(二)数学(文)试题江西省上饶市铅山县第一中学2020-2021学年高二(统招班)第三次月考数学(文)试题广东省罗定中学城东学校2023届高三上学期8月调研数学试题山东师范大学附属中学2020-2021学年高二下学期期中学分认定考试数学试题成都市玉林高中南校区2020-2021学年 高二数学(下学期)理科数学周测重庆市第八中学2020-2021学年高二下学期第二次月考数学试题湖北省武汉市部分重点中学2020-2021学年高二下学期期中联考数学试题人教A版(2019) 选修第三册 必杀技 第7.1节综合训练北师大版(2019) 选修第一册 必杀技 第六章 §1 综合训练人教A版(2019) 选修第三册 突围者 第七章 高考挑战(已下线)考点46 随机变量及其分布-备战2022年高考数学(理)一轮复习考点帮(已下线)第54讲 二项分布与正态分布(练) — 2022年高考数学一轮复习讲练测(课标全国版)人教A版(2019) 选修第三册 过关斩将 全书综合测评河南省温县第一高级中学2021-2022学年高三下学期4月月考理科数学试题天津市西青区杨柳青第一中学2021-2022学年高二下学期4月复课摸底阶段反馈数学试题(已下线)易错点14 统计、概率、离散型随机变量及其分布列山东学情2022-2023学年高二下学期3月联合考试数学试题B(已下线)第06讲 条件概率和全概率公式及应用3种常考题型(已下线)7.1.1 条件概率 (精讲)(1)北京市朝阳区中央美术学院附属实验学校2021-2022学年高二下学期期中数学试题
名校
8 . 袋内装有大小、形状完全相同的3个白球和2个黑球,从中不放回地摸球,设事件A=“第一次摸到白球”,事件B=“第二次摸到白球”,事件C=“第一次摸到黑球”,则下列说法中正确的是( )
| A.A与B是互斥事件 | B.A与B不是相互独立事件 |
| C.B与C是对立事件 | D.A与C是相互独立事件 |
您最近一年使用:0次
2022-11-25更新
|
2000次组卷
|
15卷引用:山东济南市历城第二中学2019-2020学年高一下学期学情检测数学试题
山东济南市历城第二中学2019-2020学年高一下学期学情检测数学试题广东省茂名市信宜市2023-2024学年高二上学期11月期中数学试题(已下线)专题10.2事件的相互独立性+单元测试(A卷基础篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)押第9题概率统计小题-备战2021年高考数学临考题号押题(浙江专用)北京市顺义牛栏山第一中学2022-2023学年高二上学期10月月考数学试题浙江省宁波市余姚中学2022-2023学年高二上学期期中数学试题(已下线)第04讲 随机事件、频率与概率 (高频考点,精练)(已下线)第四章 概率与统计(A卷·知识通关练)(1)(已下线)事件的相互独立性(已下线)10.2 事件的相互独立性(学案)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)第10讲 事件的相互独立性专题期末高频考点题型秒杀(已下线)第42讲 相互独立事件及频率与概率-【同步题型讲义】河北省邯郸市鸡泽县第一中学2023-2024学年高二上学期开学考数学试题山东省济南市济阳闻韶中学2023届高三上学期12月月考数学试题山东省临沂市莒南县第二中学2023-2024学年高一下学期5月月考数学试题
2020高三·全国·专题练习
名校
9 . 为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为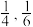 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为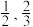 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
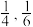 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为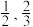 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
您最近一年使用:0次
2022-11-08更新
|
1991次组卷
|
32卷引用:专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》
(已下线)专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖山西省朔州市应县第一中学校2019-2020学年高二下学期期中数学(理)试题(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精讲)-2021年高考数学(理)一轮复习讲练测广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题(已下线)7.3 离散型随机变量的数字特征(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.4随机变量的数字特征(2)B提高练(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)(已下线)【新教材精创】7.3.2离散型随机变量的方差 -B提高练辽宁省凤城市第一中学2021-2022学年高三上学期10月月考数学试题人教A版(2019) 选修第三册 实战演练 第七章验收检测浙江省台州市九校联盟2021-2022学年高二下学期期中联考数学试题宁夏回族自治区银川一中2021-2022学年高二下学期期中考试数学(理)试题辽宁省沈阳市市级重点高中联合体2021-2022学年高二下学期期测试末数学试题江苏省苏州外国语学校2021-2022学年高二下学期期末数学试题(已下线)13.3 二项分布、超几何分布与数字特征(已下线)第70讲 随机变量及其概率分布、均值与方差(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型江苏省淮安市盱眙中学2023届高三七模数学试题(已下线)8.2.2离散型随机变量的数字特征-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)7.3.1 离散型随机变量的均值(2)(已下线)7.3.2 离散型随机变量的方差(2)(已下线)7.3.2 离散型随机变量的方差(1)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差江西省上高二中2022-2023学年高二下学期2月月考数学试题(已下线)7.3离散型随机变量的数字特征 第二练 强化考点训练江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期期中考试数学试题湖北省荆州中学2024届高三下学期第三次适应性考试数学试题【江苏专用】专题08概率与统计(第五部分)-高二下学期名校期末好题汇编(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册
名校
解题方法
10 . 甲、乙两人进行围棋比赛,比赛要求双方下满五盘棋,已知第一盘棋甲赢的概率为 ,由于心态不稳,若甲赢了上一盘棋,则下一盘棋甲赢的概率依然为
,由于心态不稳,若甲赢了上一盘棋,则下一盘棋甲赢的概率依然为 ,若甲输了上一盘棋,则下一盘棋甲赢的概率就变为
,若甲输了上一盘棋,则下一盘棋甲赢的概率就变为 .已知比赛没有和棋,且前两盘棋都是甲赢.
.已知比赛没有和棋,且前两盘棋都是甲赢.
(1)求第四盘棋甲赢的概率;
(2)求比赛结束时,甲恰好赢三盘棋的概率.
 ,由于心态不稳,若甲赢了上一盘棋,则下一盘棋甲赢的概率依然为
,由于心态不稳,若甲赢了上一盘棋,则下一盘棋甲赢的概率依然为 ,若甲输了上一盘棋,则下一盘棋甲赢的概率就变为
,若甲输了上一盘棋,则下一盘棋甲赢的概率就变为 .已知比赛没有和棋,且前两盘棋都是甲赢.
.已知比赛没有和棋,且前两盘棋都是甲赢.(1)求第四盘棋甲赢的概率;
(2)求比赛结束时,甲恰好赢三盘棋的概率.
您最近一年使用:0次
2022-11-06更新
|
3109次组卷
|
20卷引用:海南省2020届高三年级第五次模拟考试数学试题
海南省2020届高三年级第五次模拟考试数学试题海南省2020届高三高考数学五模试题(已下线)考点37 独立事件与独立重复试验(练习)-2021年高考数学复习一轮复习笔记(已下线)专题18 概率与统计综合-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)专题18 概率与统计综合-2020年高考数学(文)母题题源解密(全国Ⅱ专版)2021届高三高考必杀技之概率统计专练广东省广州市六中2022-2023学年高二上学期期中(线上)数学试题广东省广州市第六中学2022-2023学年高二上学期期中数学试题广东省佛山市三水区北博德翰外国语学校2023-2024学年高二上学期10月月考数学试题沪教版(2020) 必修第三册 同步跟踪练习 第12章 12.4.2 事件的独立性天津市崇化中学2021-2022学年高二下学期期中数学试题河北省石家庄市元氏县第四中学2021-2022学年高一下学期期末数学试题湖北省郧阳中学、恩施高中、沙市中学、随州二中、襄阳三中等五校2022-2023学年高二上学期11月联考数学试题湖北省五校2022-2023学年高二上学期11月联考数学试题辽宁省沈阳市铁路实验中学2022-2023学年高一上学期期末考试数学试题(已下线)15.3 互斥事件和独立事件(分层练习)(已下线)第42讲 相互独立事件及频率与概率-【同步题型讲义】河南省信阳市第二高级中学2023-2024学年高二上学期第二次阶段测试数学试题【课后练】 3.1.2 事件的独立性 课后作业-湘教版(2019)选择性必修第二册 第3章 概率山东省临沂市莒南县第一中学2023-2024学年高一下学期5月月考数学试题