1 . 已知函数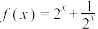 .
.
(1)用定义法证明 在
在 上单调递增;
上单调递增;
(2)求不等式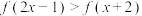 的解集;
的解集;
(3)若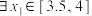 ,对
,对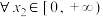 使不等式
使不等式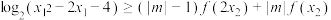 成立,求实数
成立,求实数 的取值范围.
的取值范围.
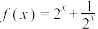 .
.(1)用定义法证明
 在
在 上单调递增;
上单调递增;(2)求不等式
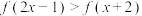 的解集;
的解集;(3)若
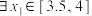 ,对
,对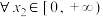 使不等式
使不等式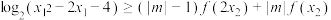 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-15更新
|
643次组卷
|
4卷引用:广东省揭阳市揭东区2023-2024学年高二上学期期中数字试题
广东省揭阳市揭东区2023-2024学年高二上学期期中数字试题陕西省渭南市大荔县2022-2023学年高一上学期期末数学试题(人教A版)陕西省渭南市大荔县2022-2023学年高一上学期期末数学试题(北师大版)(已下线)专题11 对数及对数函数压轴题-【常考压轴题】
名校
解题方法
2 . 已知函数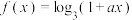 ,
,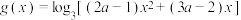 ,
, .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)已知函数 ,且方程
,且方程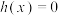 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
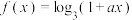 ,
,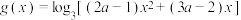 ,
, .
.(1)若
 ,求不等式
,求不等式 的解集;
的解集;(2)已知函数
 ,且方程
,且方程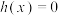 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-11-30更新
|
1334次组卷
|
5卷引用:广西桂林市第十八中学2022-2023学年高一上学期期中考试数学试题
广西桂林市第十八中学2022-2023学年高一上学期期中考试数学试题黑龙江省齐齐哈尔市2020-2021学年高二下学期期末考试数学(文)试题(已下线)专题4.11 指数函数、对数函数的综合应用大题专项训练(30道)-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)江苏省宿迁市泗阳县实验高级中学2022-2023学年高一上学期期末数学试题四川省成都市龙泉驿区东竞高级中学2023-2024学年高一上学期12月月考数学试题
名校
3 . 已知函数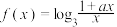 .
.
(1)若函数 的定义域为
的定义域为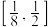 ,值域为
,值域为 ,求
,求 的值;
的值;
(2)若关于 的方程
的方程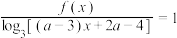 的解集中有且只有一个元素,求实数
的解集中有且只有一个元素,求实数 的取值范围.
的取值范围.
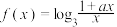 .
.(1)若函数
 的定义域为
的定义域为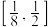 ,值域为
,值域为 ,求
,求 的值;
的值;(2)若关于
 的方程
的方程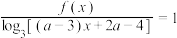 的解集中有且只有一个元素,求实数
的解集中有且只有一个元素,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-09-10更新
|
948次组卷
|
3卷引用:福建省南平市浦城县2022-2023学年高一上学期期中考试数学试题
名校
4 . 已知实数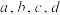 不全为0,给定函数
不全为0,给定函数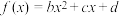 ,
,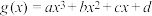 .记方程
.记方程 的解集为
的解集为 ,方程
,方程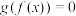 的解集为
的解集为 ,若满足
,若满足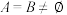 ,则称
,则称 为一对“太极函数”.问:
为一对“太极函数”.问:
(1)当 ,
, 时,验证
时,验证 是否为一对“太极函救”;
是否为一对“太极函救”;
(2)若 为一对“太极函数”,求
为一对“太极函数”,求 的值;
的值;
(3)已知 为一对“太极函数”,若
为一对“太极函数”,若 ,
, ,方程
,方程 存在正根
存在正根 ,求
,求 的取值范围(用含有
的取值范围(用含有 的代数式表示).
的代数式表示).
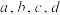 不全为0,给定函数
不全为0,给定函数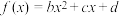 ,
,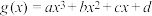 .记方程
.记方程 的解集为
的解集为 ,方程
,方程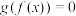 的解集为
的解集为 ,若满足
,若满足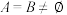 ,则称
,则称 为一对“太极函数”.问:
为一对“太极函数”.问:(1)当
 ,
, 时,验证
时,验证 是否为一对“太极函救”;
是否为一对“太极函救”;(2)若
 为一对“太极函数”,求
为一对“太极函数”,求 的值;
的值;(3)已知
 为一对“太极函数”,若
为一对“太极函数”,若 ,
, ,方程
,方程 存在正根
存在正根 ,求
,求 的取值范围(用含有
的取值范围(用含有 的代数式表示).
的代数式表示).
您最近一年使用:0次
2021-11-09更新
|
680次组卷
|
3卷引用:上海市上海中学2021-2022学年高一上学期期中数学试题
名校
5 . 已知函数 .
.
(1)若 ,求不等式
,求不等式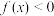 的解集;
的解集;
(2)若对任意 ,
,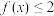 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若 ,
, ,
, 为正实数,且
为正实数,且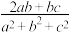 的最大值等于
的最大值等于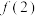 ,求实数
,求实数 的值.
的值.
 .
.(1)若
 ,求不等式
,求不等式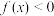 的解集;
的解集;(2)若对任意
 ,
,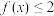 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
 ,
, ,
, 为正实数,且
为正实数,且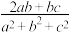 的最大值等于
的最大值等于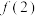 ,求实数
,求实数 的值.
的值.
您最近一年使用:0次
2021-07-21更新
|
2926次组卷
|
7卷引用:综合检测(能力篇)-2022-2023学年高一数学同步知识梳理+考点精讲精练(人教B版2019必修第一册)
(已下线)综合检测(能力篇)-2022-2023学年高一数学同步知识梳理+考点精讲精练(人教B版2019必修第一册)陕西省西安市西北工业大学附属中学2020-2021学年高一下学期第二次月考数学试题 (已下线)第3章 函数概念与性质 章末测试(提升)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第一册)(已下线)第2讲 函数的单调性与最值、奇偶性(考点讲解+分层训练)-2021-2022学年高一数学考点专项训练(人教A版2019必修第一册)(已下线)第三章 函数的概念与性质 综合检测-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)(已下线)第5章《函数概念与性质》 培优测试卷(一)-2021-2022学年高一数学上册同步培优训练系列(苏教版2019)(已下线)高一上学期期中考测试卷(基础)-《一隅三反》
名校
6 . 已知函数 ,
,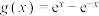 .
.
(1)求不等式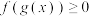 的解集;
的解集;
(2)若关于 的方程
的方程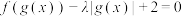 在区间
在区间 上恰有两个不同的实数解,求实数
上恰有两个不同的实数解,求实数 的取值范围.
的取值范围.
 ,
,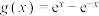 .
.(1)求不等式
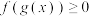 的解集;
的解集;(2)若关于
 的方程
的方程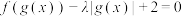 在区间
在区间 上恰有两个不同的实数解,求实数
上恰有两个不同的实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
7 . 已知函数 ,
,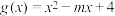 (
(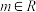 ).
).
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)若对任意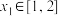 ,存在
,存在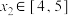 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
 ,
,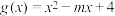 (
(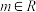 ).
).(1)当
 时,求不等式
时,求不等式 的解集;
的解集;(2)若对任意
 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)若对任意
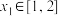 ,存在
,存在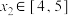 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-02-11更新
|
3127次组卷
|
18卷引用:北京市朝阳区第二外国语学院附属中学2022-2023学年高一上学期期中考试数学试题
北京市朝阳区第二外国语学院附属中学2022-2023学年高一上学期期中考试数学试题湖南省长沙市宁乡市第一高级中学2022-2023学年高二下学期期中数学试题四川省成都东部新区养马高级中学2023-2024学年高一上学期期中考试数学试题山东省淄博市第六中学2023-2024学年高一上学期期中数学试题北京市朝阳区2021-2022学年高一上学期期末数学试题黑龙江省双鸭山市第一中学2022-2023学年高一上学期10月月考数学试题山东省威海市文登区文登第一中学2020-2021学年高一上学期期末数学试题北京市第八中学2022-2023学年高一上学期期末数学试题广东省广州市第三中学2022-2023学年高一上学期期末数学试题(已下线)高一上学期期末【压轴60题考点专练】黑龙江省哈尔滨市木兰县高级中学2022-2023学年高一上学期10月月考数学试题黑龙江省双鸭山市第一中学2023-2024学年高一上学期10月月考数学试题北京市海淀区中国农业大学附属中学2024届高三上学期第一次月考(10月)数学试题(已下线)高一上学期期末数学试卷(巩固篇)-举一反三系列(已下线)专题03 函数的概念与性质3-2024年高一数学寒假作业单元合订本河北省石家庄市2023-2024学年高二下学期7月期末考试数学试题河北省石家庄十五中2023-2024学年高二下学期期末数学试题(已下线)模块二 第4套 中等模拟卷 (全真模拟高一期中备考)
名校
解题方法
8 . 对于在区间 上有意义的函数f(x),若满足对任意的
上有意义的函数f(x),若满足对任意的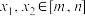 ,有
,有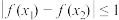 恒成立,则称f(x)在
恒成立,则称f(x)在 上是“友好”的,否则就称f(x)在
上是“友好”的,否则就称f(x)在 上是“不友好”的.现有函数
上是“不友好”的.现有函数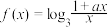
(1)当a=1时,判断函数f(x)在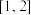 上是否“友好”;
上是否“友好”;
(2)若函数f(x)在区间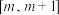 (1≤m≤2)上是“友好”的,求实数a的取值范围
(1≤m≤2)上是“友好”的,求实数a的取值范围
(3)若关于x的方程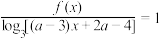 的解集中有且只有一个元素,求实数a的取值范围.
的解集中有且只有一个元素,求实数a的取值范围.
 上有意义的函数f(x),若满足对任意的
上有意义的函数f(x),若满足对任意的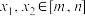 ,有
,有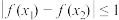 恒成立,则称f(x)在
恒成立,则称f(x)在 上是“友好”的,否则就称f(x)在
上是“友好”的,否则就称f(x)在 上是“不友好”的.现有函数
上是“不友好”的.现有函数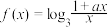
(1)当a=1时,判断函数f(x)在
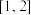 上是否“友好”;
上是否“友好”;(2)若函数f(x)在区间
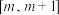 (1≤m≤2)上是“友好”的,求实数a的取值范围
(1≤m≤2)上是“友好”的,求实数a的取值范围(3)若关于x的方程
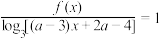 的解集中有且只有一个元素,求实数a的取值范围.
的解集中有且只有一个元素,求实数a的取值范围.
您最近一年使用:0次
2021-12-10更新
|
887次组卷
|
8卷引用:重庆市字水中学2021-2022学年高一上学期期中数学试题
重庆市字水中学2021-2022学年高一上学期期中数学试题四川省成都市第七中学2021-2022学年高一上学期期中数学试题四川省攀枝花市第十五中学校2021-2022学年高一上学期期中数学试题(已下线)第06练 幂函数、指数函数和对数函数-2022年【寒假分层作业】高一数学(苏教版2019必修第一册)苏教版(2019) 必修第一册 突围者 第6章 章末培优专练(已下线)6.3 对数函数-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)江西省宜春市宜丰县宜丰中学2022-2023学年高一下学期开学考试数学试题河南省商丘市第四高级中学2023-2024学年高一上学期期末模拟数学试题
解题方法
9 . 设 是
是 上的减函数,且对任意实数
上的减函数,且对任意实数 ,
, ,都有
,都有 ;函数
;函数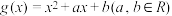
(1)判断函数 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)若 , 且存在
, 且存在 ,不等式
,不等式 成立, 求实数
成立, 求实数 的取值范围.
的取值范围.
(3)当 时, 若关于
时, 若关于 的不等式
的不等式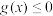 与
与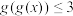 的解集相等且非空, 求
的解集相等且非空, 求 的取值范围.
的取值范围.
 是
是 上的减函数,且对任意实数
上的减函数,且对任意实数 ,
, ,都有
,都有 ;函数
;函数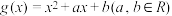
(1)判断函数
 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;(2)若
 , 且存在
, 且存在 ,不等式
,不等式 成立, 求实数
成立, 求实数 的取值范围.
的取值范围.(3)当
 时, 若关于
时, 若关于 的不等式
的不等式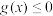 与
与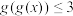 的解集相等且非空, 求
的解集相等且非空, 求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
10 . 已知集合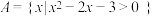 ,
,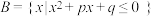 .
.
(1)若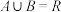 ,且
,且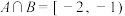 ,求实数
,求实数 及
及 的值;
的值;
(2)在(1)的条件下,若关于 的不等式组
的不等式组 没有实数解,求实数
没有实数解,求实数 的取值范围;
的取值范围;
(3)若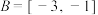 ,且关于
,且关于 的不等式;
的不等式; 的解集为
的解集为 ,求实数
,求实数 的取值范围.
的取值范围.
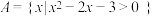 ,
,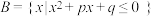 .
.(1)若
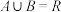 ,且
,且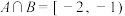 ,求实数
,求实数 及
及 的值;
的值;(2)在(1)的条件下,若关于
 的不等式组
的不等式组 没有实数解,求实数
没有实数解,求实数 的取值范围;
的取值范围;(3)若
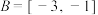 ,且关于
,且关于 的不等式;
的不等式; 的解集为
的解集为 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-10-27更新
|
2859次组卷
|
11卷引用:辽宁省大连市第四十八中学2023-2024学年高一上学期期中考试数学试题
辽宁省大连市第四十八中学2023-2024学年高一上学期期中考试数学试题上海奉贤区致远高级中学2020-2021学年高一上学期10月月考数学试题(已下线)第02讲 不等式-【提高班精讲课】2021-2022学年高一数学重点专题18讲(沪教版2020必修第一册,上海专用)辽宁省辽宁师范大学附属中学2021-2022学年高一上学期10月月考数学试题北师大版(2019) 必修第一册 名校名师卷 第四单元 一元二次函数与一元二次不等式2023版 苏教版(2019) 必修第一册 名校名师卷 第四单元 从函数观点看一元二次方程和一元二次不等式2023版 湘教版(2019) 必修第一册 名师精选卷 第四单元 从函数观点看一元二次方程、一元二次不等式上海市奉贤区致远高级中学2022-2023学年高一上学期10月月考数学试题(已下线)3.3.2.2 从函数观点看一元二次不等式-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)(已下线)第1章 集合与常用逻辑用语-【优化数学】单元测试能力卷(人教B版2019)(已下线)高考一轮单元复习验收卷·数学(一)集合、常用逻辑用语、不等式



