真题
1 . 对于一个函数 和一个点
和一个点 ,令
,令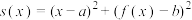 ,若
,若 是
是 取到最小值的点,则称
取到最小值的点,则称 是
是 在
在 的“最近点”.
的“最近点”.
(1)对于 ,求证:对于点
,求证:对于点 ,存在点
,存在点 ,使得点
,使得点 是
是 在
在 的“最近点”;
的“最近点”;
(2)对于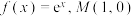 ,请判断是否存在一个点
,请判断是否存在一个点 ,它是
,它是 在
在 的“最近点”,且直线
的“最近点”,且直线 与
与 在点
在点 处的切线垂直;
处的切线垂直;
(3)已知 在定义域R上存在导函数
在定义域R上存在导函数 ,且函数
,且函数  在定义域R上恒正,设点
在定义域R上恒正,设点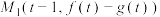 ,
,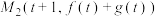 .若对任意的
.若对任意的 ,存在点
,存在点 同时是
同时是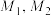 在
在 的“最近点”,试判断
的“最近点”,试判断 的单调性.
的单调性.
 和一个点
和一个点 ,令
,令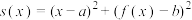 ,若
,若 是
是 取到最小值的点,则称
取到最小值的点,则称 是
是 在
在 的“最近点”.
的“最近点”.(1)对于
 ,求证:对于点
,求证:对于点 ,存在点
,存在点 ,使得点
,使得点 是
是 在
在 的“最近点”;
的“最近点”;(2)对于
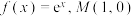 ,请判断是否存在一个点
,请判断是否存在一个点 ,它是
,它是 在
在 的“最近点”,且直线
的“最近点”,且直线 与
与 在点
在点 处的切线垂直;
处的切线垂直;(3)已知
 在定义域R上存在导函数
在定义域R上存在导函数 ,且函数
,且函数  在定义域R上恒正,设点
在定义域R上恒正,设点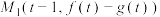 ,
,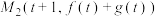 .若对任意的
.若对任意的 ,存在点
,存在点 同时是
同时是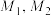 在
在 的“最近点”,试判断
的“最近点”,试判断 的单调性.
的单调性.
您最近一年使用:0次
真题
解题方法
2 . 已知双曲线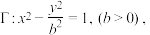 左右顶点分别为
左右顶点分别为 ,过点
,过点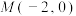 的直线
的直线 交双曲线
交双曲线 于
于 两点.
两点.
(1)若离心率 时,求
时,求 的值.
的值.
(2)若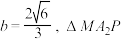 为等腰三角形时,且点
为等腰三角形时,且点 在第一象限,求点
在第一象限,求点 的坐标.
的坐标.
(3)连接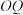 并延长,交双曲线
并延长,交双曲线 于点
于点 ,若
,若 ,求
,求 的取值范围.
的取值范围.
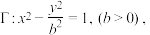 左右顶点分别为
左右顶点分别为 ,过点
,过点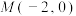 的直线
的直线 交双曲线
交双曲线 于
于 两点.
两点.(1)若离心率
 时,求
时,求 的值.
的值.(2)若
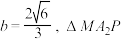 为等腰三角形时,且点
为等腰三角形时,且点 在第一象限,求点
在第一象限,求点 的坐标.
的坐标.(3)连接
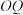 并延长,交双曲线
并延长,交双曲线 于点
于点 ,若
,若 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
真题
解题方法
3 . 已知函数 的定义域为R,定义集合
的定义域为R,定义集合 ,在使得
,在使得 的所有
的所有 中,下列成立的是( )
中,下列成立的是( )
 的定义域为R,定义集合
的定义域为R,定义集合 ,在使得
,在使得 的所有
的所有 中,下列成立的是( )
中,下列成立的是( )A.存在 是偶函数 是偶函数 | B.存在 在 在 处取最大值 处取最大值 |
C.存在 是严格增函数 是严格增函数 | D.存在 在 在 处取到极小值 处取到极小值 |
您最近一年使用:0次
名校
解题方法
4 . 已知函数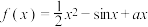 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)①求证: 有且仅有一个极值点;
有且仅有一个极值点;
②当 时,设
时,设 的极值点为
的极值点为 ,若
,若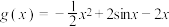 .求证:
.求证: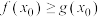
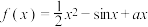 .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)①求证:
 有且仅有一个极值点;
有且仅有一个极值点;②当
 时,设
时,设 的极值点为
的极值点为 ,若
,若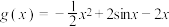 .求证:
.求证: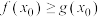
您最近一年使用:0次
2024-06-08更新
|
642次组卷
|
3卷引用:专题15 导数与三角函数联袂【练】
名校
解题方法
5 . 已知抛物线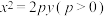 上的动点到其焦点的距离的最小值为
上的动点到其焦点的距离的最小值为 .
.
(1)求抛物线的方程;
(2)过抛物线上一点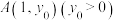 作抛物线的切线,分别交
作抛物线的切线,分别交 轴于点
轴于点 ,交
,交 轴于点
轴于点 .点
.点 在抛物线上,点
在抛物线上,点 在线段
在线段 上,满足能
上,满足能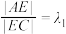 ;点
;点 在线段
在线段 上,满足
上,满足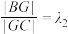 ,且
,且 ,线段
,线段 与
与 交于点
交于点 ,当点
,当点 在抛物线上移动时,求点
在抛物线上移动时,求点 的轨迹方程
的轨迹方程 .
.
(3)将 向左平移
向左平移 个单位,得到
个单位,得到 ,已知
,已知 ,
, ,过点
,过点 作直线
作直线 交
交 于
于 .设
.设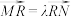 ,求
,求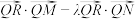 的值
的值
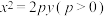 上的动点到其焦点的距离的最小值为
上的动点到其焦点的距离的最小值为 .
.(1)求抛物线的方程;
(2)过抛物线上一点
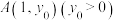 作抛物线的切线,分别交
作抛物线的切线,分别交 轴于点
轴于点 ,交
,交 轴于点
轴于点 .点
.点 在抛物线上,点
在抛物线上,点 在线段
在线段 上,满足能
上,满足能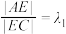 ;点
;点 在线段
在线段 上,满足
上,满足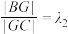 ,且
,且 ,线段
,线段 与
与 交于点
交于点 ,当点
,当点 在抛物线上移动时,求点
在抛物线上移动时,求点 的轨迹方程
的轨迹方程 .
.(3)将
 向左平移
向左平移 个单位,得到
个单位,得到 ,已知
,已知 ,
, ,过点
,过点 作直线
作直线 交
交 于
于 .设
.设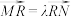 ,求
,求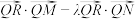 的值
的值
您最近一年使用:0次
2024-06-04更新
|
717次组卷
|
3卷引用:专题9 考前押题大猜想41-45
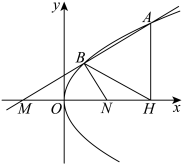
6 . 如图,在平面直角坐标系中, 和
和 是
是 轴上关于原点对称的两个点,过点
轴上关于原点对称的两个点,过点 倾斜角为
倾斜角为 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且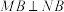 .
. 为
为 的焦点,求证:
的焦点,求证: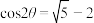 ;
;
(2)过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若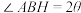 ,求直线
,求直线 的方程.
的方程.
 和
和 是
是 轴上关于原点对称的两个点,过点
轴上关于原点对称的两个点,过点 倾斜角为
倾斜角为 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且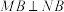 .
.
 为
为 的焦点,求证:
的焦点,求证: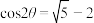 ;
;(2)过点
 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,若
,若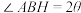 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-06-03更新
|
499次组卷
|
3卷引用:第一套 艺体生新高考全真模拟 (三模重组卷)
解题方法
7 . 法国数学家弗朗索瓦·韦达发现了一元二次方程的根与系数之间的关系,将其推广到高次方程,并在其著作《论方程的识别与订正》中正式发表,后来人们把这个关系称为韦达定理,即如果 是关于x的实系数一元n次方程
是关于x的实系数一元n次方程 在复数集C内的n个根,则
在复数集C内的n个根,则
试运用韦达定理解决下列问题:
(1)已知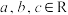 ,
, ,
, ,求
,求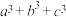 的最小值;
的最小值;
(2)已知 ,关于x的方程
,关于x的方程 有三个实数根,其中至少有一个实效根在区间
有三个实数根,其中至少有一个实效根在区间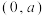 内,求
内,求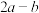 的最大值.
的最大值.
 是关于x的实系数一元n次方程
是关于x的实系数一元n次方程 在复数集C内的n个根,则
在复数集C内的n个根,则
试运用韦达定理解决下列问题:
(1)已知
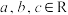 ,
, ,
, ,求
,求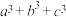 的最小值;
的最小值;(2)已知
 ,关于x的方程
,关于x的方程 有三个实数根,其中至少有一个实效根在区间
有三个实数根,其中至少有一个实效根在区间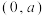 内,求
内,求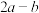 的最大值.
的最大值.
您最近一年使用:0次
解题方法
8 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且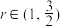 .
.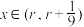 时,
时,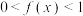 ;
;
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得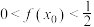 ,然后在点
,然后在点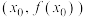 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列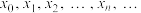 .
.
①当 时,证明:
时,证明: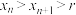 ;
;
②根据①的结论,运用数学归纳法可以证得: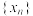 为递减数列,且
为递减数列,且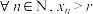 .请以此为前提条件,证明:
.请以此为前提条件,证明: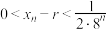 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且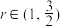 .
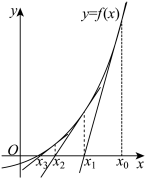
.
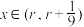 时,
时,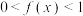 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得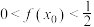 ,然后在点
,然后在点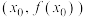 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列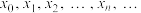 .
.①当
 时,证明:
时,证明: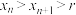 ;
;②根据①的结论,运用数学归纳法可以证得:
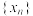 为递减数列,且
为递减数列,且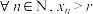 .请以此为前提条件,证明:
.请以此为前提条件,证明: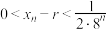 .
.
您最近一年使用:0次
解题方法
9 . 已知函数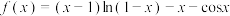 .
.
(1)求函数 在区间
在区间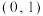 上的极值点的个数.
上的极值点的个数.
(2)“ ”是一个求和符号,例如
”是一个求和符号,例如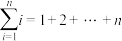 ,
, ,等等.英国数学家布鲁克·泰勒发现,当
,等等.英国数学家布鲁克·泰勒发现,当 时,
时, ,这就是麦克劳林展开式在三角函数上的一个经典应用.
,这就是麦克劳林展开式在三角函数上的一个经典应用.
证明:(i)当 时,对
时,对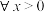 ,都有
,都有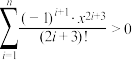 ;
;
(ii)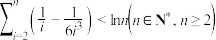 .
.
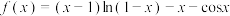 .
.(1)求函数
 在区间
在区间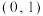 上的极值点的个数.
上的极值点的个数.(2)“
 ”是一个求和符号,例如
”是一个求和符号,例如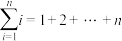 ,
, ,等等.英国数学家布鲁克·泰勒发现,当
,等等.英国数学家布鲁克·泰勒发现,当 时,
时, ,这就是麦克劳林展开式在三角函数上的一个经典应用.
,这就是麦克劳林展开式在三角函数上的一个经典应用.证明:(i)当
 时,对
时,对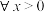 ,都有
,都有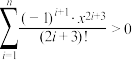 ;
;(ii)
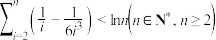 .
.
您最近一年使用:0次
名校
10 . 阅读材料一:“装错信封问题”是由数学家约翰·伯努利(Johann Bernoulli,1667~1748)的儿子丹尼尔·伯努利提出来的,大意如下:一个人写了 封不同的信及相应的
封不同的信及相应的 个不同的信封,他把这
个不同的信封,他把这 封信都装错了信封,问都装错信封的这一情况有多少种?后来瑞士数学家欧拉(Leonhard Euler,1707~1783)给出了解答:记都装错
封信都装错了信封,问都装错信封的这一情况有多少种?后来瑞士数学家欧拉(Leonhard Euler,1707~1783)给出了解答:记都装错 封信的情况为
封信的情况为 种,可以用全排列
种,可以用全排列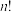 减去有装正确的情况种数,结合容斥原理可得公式:
减去有装正确的情况种数,结合容斥原理可得公式: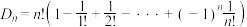 ,其中
,其中 .
.
阅读材料二:英国数学家泰勒发现的泰勒公式有如下特殊形式:当 在
在 处
处 阶可导,则有:
阶可导,则有: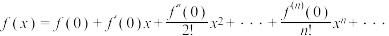 ,注
,注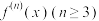 表示
表示 的
的 阶导数,该公式也称麦克劳林公式.阅读以上材料后请完成以下问题:
阶导数,该公式也称麦克劳林公式.阅读以上材料后请完成以下问题:
(1)求出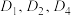 的值;
的值;
(2)估算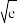 的大小(保留小数点后2位),并给出用
的大小(保留小数点后2位),并给出用 和
和 表示
表示 的估计公式;
的估计公式;
(3)求证: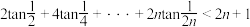 ,其中
,其中 .
.
 封不同的信及相应的
封不同的信及相应的 个不同的信封,他把这
个不同的信封,他把这 封信都装错了信封,问都装错信封的这一情况有多少种?后来瑞士数学家欧拉(Leonhard Euler,1707~1783)给出了解答:记都装错
封信都装错了信封,问都装错信封的这一情况有多少种?后来瑞士数学家欧拉(Leonhard Euler,1707~1783)给出了解答:记都装错 封信的情况为
封信的情况为 种,可以用全排列
种,可以用全排列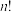 减去有装正确的情况种数,结合容斥原理可得公式:
减去有装正确的情况种数,结合容斥原理可得公式: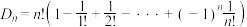 ,其中
,其中 .
.阅读材料二:英国数学家泰勒发现的泰勒公式有如下特殊形式:当
 在
在 处
处 阶可导,则有:
阶可导,则有: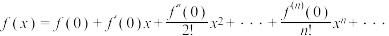 ,注
,注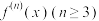 表示
表示 的
的 阶导数,该公式也称麦克劳林公式.阅读以上材料后请完成以下问题:
阶导数,该公式也称麦克劳林公式.阅读以上材料后请完成以下问题:(1)求出
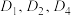 的值;
的值;(2)估算
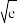 的大小(保留小数点后2位),并给出用
的大小(保留小数点后2位),并给出用 和
和 表示
表示 的估计公式;
的估计公式;(3)求证:
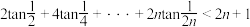 ,其中
,其中 .
.
您最近一年使用:0次



