2023·全国·模拟预测
名校
1 . 已知函数 ,
, .
.
(1)若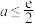 ,证明:
,证明: 在
在 上单调递增.
上单调递增.
(2)若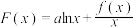 存在两个极小值点
存在两个极小值点
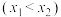 .
.
①求实数 的取值范围;
的取值范围;
②试比较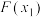 与
与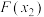 的大小.
的大小.
 ,
, .
.(1)若
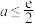 ,证明:
,证明: 在
在 上单调递增.
上单调递增.(2)若
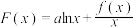 存在两个极小值点
存在两个极小值点
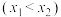 .
.①求实数
 的取值范围;
的取值范围;②试比较
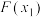 与
与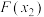 的大小.
的大小.
您最近一年使用:0次
2023-03-19更新
|
777次组卷
|
3卷引用:2023年普通高等学校招生全国统一考试数学猜题卷(八)
(已下线)2023年普通高等学校招生全国统一考试数学猜题卷(八)江苏省四校(无锡市辅仁高级中学、江阴高中、宜兴一中、常州市北郊中学)2022-2023学年高三下学期4月阶段性测试数学试题浙江省嘉兴市桐乡第一中学2023届高三下学期5月适应性测试数学试题
解题方法
2 . 已知函数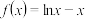 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数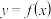 的图象与
的图象与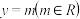 的图象交于
的图象交于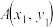 ,
,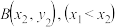 两点,证明:
两点,证明: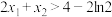 .
.
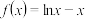 .
.(1)求函数
 的单调区间;
的单调区间;(2)若函数
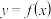 的图象与
的图象与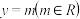 的图象交于
的图象交于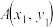 ,
,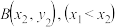 两点,证明:
两点,证明: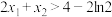 .
.
您最近一年使用:0次
2022-04-26更新
|
1105次组卷
|
3卷引用:浙江省A9协作体2021-2022学年高二下学期期中联考数学试题
浙江省A9协作体2021-2022学年高二下学期期中联考数学试题(已下线)专题06 极值点偏移问题-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)浙江省嘉兴市第五高级中学2022-2023学年高二下学期期中数学试题
名校
解题方法
3 . 已知函数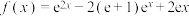 .
.
(1)若函数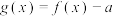 有三个零点,求a的取值范围.
有三个零点,求a的取值范围.
(2)若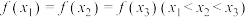 ,证明:
,证明: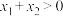 .
.
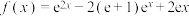 .
.(1)若函数
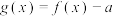 有三个零点,求a的取值范围.
有三个零点,求a的取值范围.(2)若
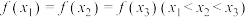 ,证明:
,证明: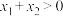 .
.
您最近一年使用:0次
2022-04-08更新
|
1298次组卷
|
3卷引用:河南省(豫北重点高中)2021-2022学年高三下学期4月份模拟考试理科数学试题
4 . 设函数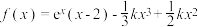 .
.
(1)若 ,求
,求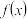 的单调区间;
的单调区间;
(2)若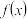 存在三个极值点
存在三个极值点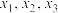 ,且
,且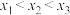 ,求
,求 的取值范围,并证明:
的取值范围,并证明: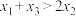 .
.
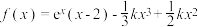 .
.(1)若
 ,求
,求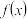 的单调区间;
的单调区间;(2)若
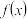 存在三个极值点
存在三个极值点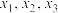 ,且
,且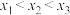 ,求
,求 的取值范围,并证明:
的取值范围,并证明: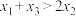 .
.
您最近一年使用:0次
2022-02-22更新
|
486次组卷
|
8卷引用:河南省洛阳市2019-2020学年高三上学期第一次统一考试(1月)数学(理)试题
河南省洛阳市2019-2020学年高三上学期第一次统一考试(1月)数学(理)试题(已下线)第三章+导数及其应用(能力提升)-2020-2021学年高二数学单元测试定心卷(人教版选修1-1)(已下线)第三章 导数及其应用(能力提升)-2020-2021学年高二数学单元测试定心卷(苏教版选修1-1)(已下线)专题13 第二章 复习与检测 核心素养练习 -【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第二册)(已下线)第03讲 极值点偏移:加法类型-突破2022年新高考数学导数压轴解答题精选精练(已下线)专题19利用导数证明不等式(讲)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题3-9 利用导函数研究极值点偏移问题(已下线)专题07 导数的综合问题(2)
名校
解题方法
5 . 已知函数 .
.
(1)求函数 的极值点;
的极值点;
(2)若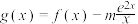 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
 .
.(1)求函数
 的极值点;
的极值点;(2)若
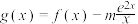 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-10-14更新
|
1691次组卷
|
10卷引用:山东省2021-2022学年高三10月“山东学情”联考数学试题A
山东省2021-2022学年高三10月“山东学情”联考数学试题A山东省2021-2022学年高三10月“山东学情”联考数学试题B江西省赣州市赣县第三中学2022届高三上学期期中适应考试数学(文)试题河南省林州市第一中学2021-2022学年高二下学期2月开学考数学(文)试题陕西省咸阳市武功县普集高中2022届高三加强班下学期3月月考理科数学试题广西桂林市普通高中联盟2021-2022学年高二下学期期中数学(理)试题江西省赣州市定南中学2021-2022学年高二5月考数学(理)试题山东省枣庄市滕州市滕州市第一中学2022-2023学年高三上学期10月月考数学试题广西钦州市第四中学2021-2022学年高二下学期2月月考数学试题(理科)新疆皮山县高级中学2022-2023学年高二下学期期末考试数学试题
名校
6 . 已知函数 (
(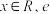 为自然数对数的底数).
为自然数对数的底数).
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 在
在 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
 (
(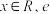 为自然数对数的底数).
为自然数对数的底数).(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)若函数
 在
在 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-09-11更新
|
1437次组卷
|
18卷引用:2018-2019人教高中数学选修1-1:第三章 章末评估验收(三)
2018-2019人教高中数学选修1-1:第三章 章末评估验收(三)云南省昆明市民族中学2019-2020学年高三上学期10月适应性月考数学试题福建省莆田市莆田第七中学2019-2020学年高三上学期期中数学(文)试题青海省西宁市第十四中学2019-2020学年高二上学期期末数学(文)试题甘肃省民乐县第一中学2019-2020学年高三3月线上考试数学(理)试题广西蒙山县蒙山中学2019-2020学年高二4月网站在线考试数学(理)试题西藏自治区林芝市第二中学2019-2020学年高二下学期第一次月考数学(理科)试题河南省新乡市辉县市第二高级中学2019-2020学年高二下学期期中考试数学(理)试题(已下线)第14讲 导数在研究函数中的应用-2021年新高考数学一轮专题复习(新高考专版)宁夏青铜峡市高级中学2021届高三上学期第二次月考数学(理)试题新疆哈密市第八中学2019-2020学年高二下学期期末考试数学(文)试题广东省湛江市第二高级中学2021届高三下学期3月模拟数学试题重庆市万州纯阳中学2020-2021学年高二下学期第一次月考数学试题(已下线)专题2.6 函数的单调性与最值-重难点题型精练-2022年高考数学一轮复习举一反三系列(新高考地区专用)天津市第三中学2021-2022学年高三上学期10月阶段性检测数学试题广西南宁高新技术产业开发区桂鼎学校2021-2022学年高二下学期3月月考数学(理)试题内蒙古自治区赤峰市松山区赤峰新城红旗中学2023-2024学年高二下学期4月月考数学试题陕西省渭南市华州区咸林中学2023-2024学年高二下学期期中考试数学试题
7 . 已知函数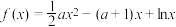 ,
,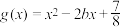 .
.
(1)若 时函数
时函数 有极小值,试确定a的取值范围;
有极小值,试确定a的取值范围;
(2)当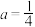 时,函数
时,函数 在
在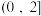 上的最大值为
上的最大值为 ,若存在
,若存在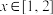 ,使得
,使得 成立,求实数b的取值范围.
成立,求实数b的取值范围.
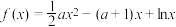 ,
,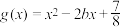 .
.(1)若
 时函数
时函数 有极小值,试确定a的取值范围;
有极小值,试确定a的取值范围;(2)当
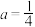 时,函数
时,函数 在
在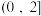 上的最大值为
上的最大值为 ,若存在
,若存在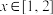 ,使得
,使得 成立,求实数b的取值范围.
成立,求实数b的取值范围.
您最近一年使用:0次
2021-07-25更新
|
553次组卷
|
3卷引用:天津市第三中学2020-2021学年高二下学期期中数学试题
天津市第三中学2020-2021学年高二下学期期中数学试题(已下线)一轮大题专练12—导数(有解问题2)-2022届高三数学一轮复习天津市北京师范大学天津附属中学2021-2022学年高三上学期第一次月考数学试题
8 . 已知函数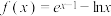 .
.
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若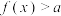 恒成立.求a的取值范围.
恒成立.求a的取值范围.
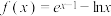 .
.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)若
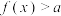 恒成立.求a的取值范围.
恒成立.求a的取值范围.
您最近一年使用:0次
2021-07-21更新
|
650次组卷
|
2卷引用:云南省部分名校2020-2021学年高二下学期期末联考数学(文)试题
解题方法
9 . 已知函数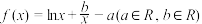 有最小值M,且
有最小值M,且 .
.
(Ⅰ)求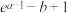 的最大值;
的最大值;
(Ⅱ)当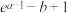 取得最大值时,设
取得最大值时,设 ,
, 有两个零点为
有两个零点为 ,证明:
,证明: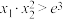 .
.
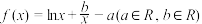 有最小值M,且
有最小值M,且 .
.(Ⅰ)求
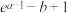 的最大值;
的最大值;(Ⅱ)当
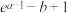 取得最大值时,设
取得最大值时,设 ,
, 有两个零点为
有两个零点为 ,证明:
,证明: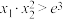 .
.
您最近一年使用:0次
2021-05-12更新
|
2603次组卷
|
6卷引用:四川省攀枝花市2021届高三二模考试数学(文)试题
四川省攀枝花市2021届高三二模考试数学(文)试题(已下线)第四章 导数专练7—双变量与极值点偏移问题(1)-2022届高三数学一轮复习(已下线)第05讲 极值点偏移:平方型-突破2022年新高考数学导数压轴解答题精选精练(已下线)第08讲 双变量不等式:转化为单变量问题-突破2022年新高考数学导数压轴解答题精选精练(已下线)第06讲 极值点偏移:乘积型-突破2022年新高考数学导数压轴解答题精选精练(已下线)专题05 极值点偏移问题与拐点偏移问题-1
2019高三·全国·专题练习
名校
10 . 已知函数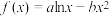 ,
,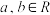 ,函数
,函数 在
在 处与直线
处与直线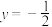 相切.
相切.
(1)求实数a,b的值;
(2)判断函数 在
在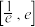 上的单调性.
上的单调性.
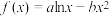 ,
,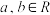 ,函数
,函数 在
在 处与直线
处与直线 相切.
相切.(1)求实数a,b的值;
(2)判断函数
 在
在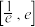 上的单调性.
上的单调性.
您最近一年使用:0次
2021-04-21更新
|
1771次组卷
|
12卷引用:2019年8月9日《每日一题》2020年高考一轮复习(文科)—— 导数与函数的单调性(2)
(已下线)2019年8月9日《每日一题》2020年高考一轮复习(文科)—— 导数与函数的单调性(2)江西省赣州市2019-2020学年高二下学期线上教学检测数学(理)试题(已下线)第五章++一元函数的导数及其应用1(能力提升)-2020-2021学年高二数学单元测试定心卷(人教A版2019选择性必修第二册)(已下线)第三章+导数及其应用(能力提升)-2020-2021学年高二数学单元测试定心卷(人教版选修1-1)(已下线)第三章 导数及其应用(能力提升)-2020-2021学年高二数学单元测试定心卷(苏教版选修1-1)(已下线)第一章 导数及其应用(能力提升)-2020-2021学年高二数学单元测试定心卷(人教版选修2-2)(已下线)专题13 第二章 复习与检测 核心素养练习 -【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第二册)第六章 导数及其应用(A基础卷)-新教材2020-2021学年高二数学尖子生培优AB卷(人教B版2019选择性必修第三册)四川省仁寿第一中学校南校区2020-2021学年高二第三次质量检测(6月月考)数学(文)试题河南省教育联盟2021-2022学年高二下学期4月联考文科数学试题河南省项城市第三高级中学2022-2023学年高三上学期第一次调研考试数学(文)试题宁夏银川市第六中学2022-2023学年高二下学期期末考试数学(文)试题



