1 . 我们把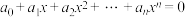 (其中
(其中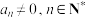 )称为一元
)称为一元 次多项式方程.代数基本定理:任何一元
次多项式方程.代数基本定理:任何一元 次复系数多项式方程(即
次复系数多项式方程(即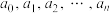 为实数)在复数集内至少有一个复数根;由此推得,任何一元
为实数)在复数集内至少有一个复数根;由此推得,任何一元 次复系数多项式方程在复数集内有且仅有
次复系数多项式方程在复数集内有且仅有 个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元
个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元 次复系数多项式在复数集内一定可以分解因式,转化为
次复系数多项式在复数集内一定可以分解因式,转化为 个一元一次多项式的积.即
个一元一次多项式的积.即 ,其中
,其中 ,
, 为方程
为方程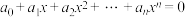 的根.进一步可以推出:在实系数范围内(即
的根.进一步可以推出:在实系数范围内(即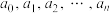 为实数),方程
为实数),方程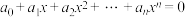 有实数根,则多项式
有实数根,则多项式 必可分解因式.例如:观察可知,
必可分解因式.例如:观察可知, 是方程
是方程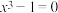 的一个根,则
的一个根,则 一定是多项式
一定是多项式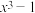 的一个因式,即
的一个因式,即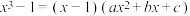 ,由待定系数法可知,
,由待定系数法可知, .
.
(1)在复数集内解方程: ;
;
(2)设 ,其中
,其中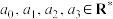 ,且
,且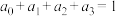 .
.
(i)分解因式: ;
;
(ii)记点 是
是 的图象与直线
的图象与直线 在第一象限内离原点最近的交点.求证:当
在第一象限内离原点最近的交点.求证:当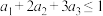 时,
时,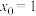 .
.
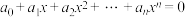 (其中
(其中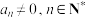 )称为一元
)称为一元 次多项式方程.代数基本定理:任何一元
次多项式方程.代数基本定理:任何一元 次复系数多项式方程(即
次复系数多项式方程(即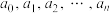 为实数)在复数集内至少有一个复数根;由此推得,任何一元
为实数)在复数集内至少有一个复数根;由此推得,任何一元 次复系数多项式方程在复数集内有且仅有
次复系数多项式方程在复数集内有且仅有 个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元
个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元 次复系数多项式在复数集内一定可以分解因式,转化为
次复系数多项式在复数集内一定可以分解因式,转化为 个一元一次多项式的积.即
个一元一次多项式的积.即 ,其中
,其中 ,
, 为方程
为方程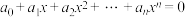 的根.进一步可以推出:在实系数范围内(即
的根.进一步可以推出:在实系数范围内(即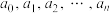 为实数),方程
为实数),方程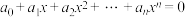 有实数根,则多项式
有实数根,则多项式 必可分解因式.例如:观察可知,
必可分解因式.例如:观察可知, 是方程
是方程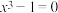 的一个根,则
的一个根,则 一定是多项式
一定是多项式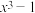 的一个因式,即
的一个因式,即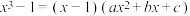 ,由待定系数法可知,
,由待定系数法可知, .
.(1)在复数集内解方程:
 ;
;(2)设
 ,其中
,其中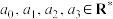 ,且
,且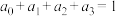 .
.(i)分解因式:
 ;
;(ii)记点
 是
是 的图象与直线
的图象与直线 在第一象限内离原点最近的交点.求证:当
在第一象限内离原点最近的交点.求证:当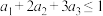 时,
时,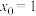 .
.
您最近半年使用:0次
名校
2 . 函数 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点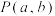 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数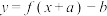 为奇函数.已知函数
为奇函数.已知函数 .
.
(1)若函数 的对称中心为
的对称中心为 ,求函数
,求函数 的解析式.
的解析式.
(2)由代数基本定理可以得到:任何一元 次复系数多项式
次复系数多项式 在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程
在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程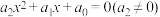 ,在复数集内的根为
,在复数集内的根为 ,
, ,则方程
,则方程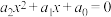 可变形为
可变形为 ,展开得:
,展开得: 则有
则有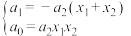 ,即
,即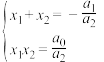 ,类比上述推理方法可得实系数一元三次方程根与系数的关系.
,类比上述推理方法可得实系数一元三次方程根与系数的关系.
①若 ,方程
,方程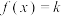 在复数集内的根为
在复数集内的根为 ,当
,当 时,求
时,求 的最大值;
的最大值;
②若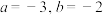 ,函数
,函数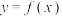 的零点分别为
的零点分别为 ,求
,求 的值.
的值.
 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数 的图象关于点
的图象关于点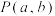 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数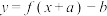 为奇函数.已知函数
为奇函数.已知函数 .
.(1)若函数
 的对称中心为
的对称中心为 ,求函数
,求函数 的解析式.
的解析式.(2)由代数基本定理可以得到:任何一元
 次复系数多项式
次复系数多项式 在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程
在复数集中可以分解为n个一次因式的乘积.进而,一元n次多项式方程有n个复数根(重根按重数计).如设实系数一元二次方程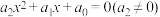 ,在复数集内的根为
,在复数集内的根为 ,
, ,则方程
,则方程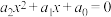 可变形为
可变形为 ,展开得:
,展开得: 则有
则有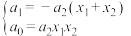 ,即
,即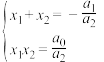 ,类比上述推理方法可得实系数一元三次方程根与系数的关系.
,类比上述推理方法可得实系数一元三次方程根与系数的关系.①若
 ,方程
,方程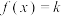 在复数集内的根为
在复数集内的根为 ,当
,当 时,求
时,求 的最大值;
的最大值;②若
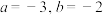 ,函数
,函数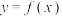 的零点分别为
的零点分别为 ,求
,求 的值.
的值.
您最近半年使用:0次
3 . 对于非空集合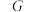 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在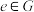 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得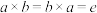 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意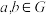 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群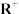 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群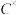 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
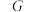 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
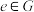 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得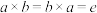 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意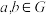 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
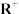 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群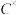 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近半年使用:0次
解题方法
4 . 设M是由复数组成的集合,对M的一个子集A,若存在复平面上的一个圆,使得A的所有数在复平面上对应的点都在圆内或圆周上,且 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
(1)判断 是否是
是否是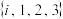 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;
(2)设复数z满足 ,其中
,其中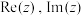 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: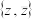 是
是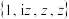 的“可分离子集”当且仅当
的“可分离子集”当且仅当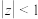 .
.
 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.(1)判断
 是否是
是否是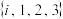 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;(2)设复数z满足
 ,其中
,其中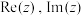 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: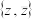 是
是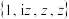 的“可分离子集”当且仅当
的“可分离子集”当且仅当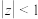 .
.
您最近半年使用:0次
5 . 对于函数 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为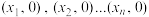 ,记
,记 为数列
为数列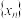 的第n项,则称数列
的第n项,则称数列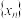 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为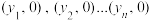 ,记
,记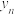 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”
(1)设函数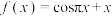 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.
(2)设函数 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.
(3)设复数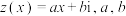 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
 ,分别在
,分别在 处作函数
处作函数 的切线,记切线与
的切线,记切线与 轴的交点分别为
轴的交点分别为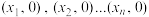 ,记
,记 为数列
为数列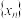 的第n项,则称数列
的第n项,则称数列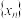 为函数
为函数 的“切线-
的“切线- 轴数列”,同理记切线与
轴数列”,同理记切线与 轴的交点分别为
轴的交点分别为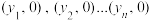 ,记
,记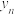 为数列
为数列 的第n项,则称数列
的第n项,则称数列 为函数
为函数 的“切线-
的“切线- 轴数列”
轴数列”(1)设函数
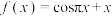 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,记
,记 为
为 的前n项和,求
的前n项和,求 .
.(2)设函数
 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,猜想
,猜想 的通项公式并证明你的结论.
的通项公式并证明你的结论.(3)设复数
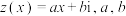 均为不为0的实数,记
均为不为0的实数,记 为
为 的共轭复数,设
的共轭复数,设 ,记
,记 “切线-
“切线- 轴数列”为
轴数列”为 ,求证:对于任意的不为0的实数
,求证:对于任意的不为0的实数 ,总有
,总有 成立.
成立.
您最近半年使用:0次
解题方法
6 . 已知i是虚数单位,a,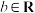 ,设复数
,设复数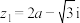 ,
, ,
,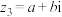 ,且
,且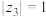 .
.
(1)若 为纯虚数,求
为纯虚数,求 ;
;
(2)若复数 ,
,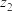 在复平面上对应的点分别为A,B,且O为复平面的坐标原点.
在复平面上对应的点分别为A,B,且O为复平面的坐标原点.
①是否存在实数a,b,使向量 逆时针旋转
逆时针旋转 后与向量
后与向量 重合,如果存在,求实数a,b的值;如果不存在,请说明理由;
重合,如果存在,求实数a,b的值;如果不存在,请说明理由;
②若O,A,B三点不共线,记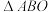 的面积为
的面积为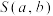 ,求
,求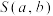 及其最大值.
及其最大值.
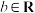 ,设复数
,设复数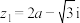 ,
, ,
,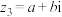 ,且
,且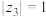 .
.(1)若
 为纯虚数,求
为纯虚数,求 ;
;(2)若复数
 ,
,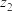 在复平面上对应的点分别为A,B,且O为复平面的坐标原点.
在复平面上对应的点分别为A,B,且O为复平面的坐标原点.①是否存在实数a,b,使向量
 逆时针旋转
逆时针旋转 后与向量
后与向量 重合,如果存在,求实数a,b的值;如果不存在,请说明理由;
重合,如果存在,求实数a,b的值;如果不存在,请说明理由;②若O,A,B三点不共线,记
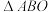 的面积为
的面积为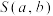 ,求
,求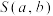 及其最大值.
及其最大值.
您最近半年使用:0次
7 . 通过平面直角坐标系,我们可以用有序实数对表示向量.类似的,我们可以把有序复数对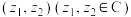 看作一个向量,记
看作一个向量,记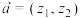 ,则称
,则称 为复向量.类比平面向量的相关运算法则,对于
为复向量.类比平面向量的相关运算法则,对于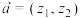 ,
,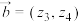 ,
, 、
、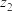 、
、 、
、 、
、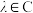 ,我们有如下运算法则:
,我们有如下运算法则:
①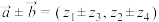 ; ②
; ② ;
;
③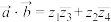 ; ④
; ④ .
.
(1)设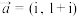 ,
,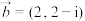 ,求
,求 和
和 .
.
(2)由平面向量的数量积满足的运算律,我们类比得到复向量的相关结论:
①
② ③
③ .
.
试判断这三个结论是否正确,并对正确的结论予以证明.
(3)若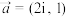 ,集合
,集合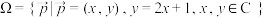 ,
,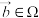 .对于任意的
.对于任意的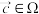 ,求出满足条件
,求出满足条件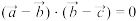 的
的 ,并将此时的
,并将此时的 记为
记为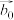 ,证明对任意的
,证明对任意的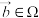 ,不等式
,不等式 恒成立.
恒成立.
根据对上述问题的解答过程,试写出一个一般性的命题(不需要证明).
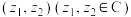 看作一个向量,记
看作一个向量,记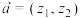 ,则称
,则称 为复向量.类比平面向量的相关运算法则,对于
为复向量.类比平面向量的相关运算法则,对于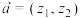 ,
,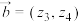 ,
, 、
、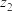 、
、 、
、 、
、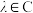 ,我们有如下运算法则:
,我们有如下运算法则:①
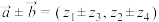 ; ②
; ② ;
;③
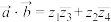 ; ④
; ④ .
.(1)设
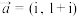 ,
,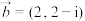 ,求
,求 和
和 .
.(2)由平面向量的数量积满足的运算律,我们类比得到复向量的相关结论:
①

②
 ③
③ .
.试判断这三个结论是否正确,并对正确的结论予以证明.
(3)若
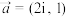 ,集合
,集合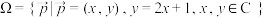 ,
,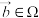 .对于任意的
.对于任意的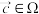 ,求出满足条件
,求出满足条件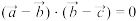 的
的 ,并将此时的
,并将此时的 记为
记为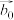 ,证明对任意的
,证明对任意的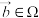 ,不等式
,不等式 恒成立.
恒成立.根据对上述问题的解答过程,试写出一个一般性的命题(不需要证明).
您最近半年使用:0次
名校
8 . 设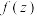 是一个关于复数z的表达式,若
是一个关于复数z的表达式,若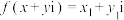 (其中x,y,
(其中x,y, ,
,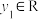

 为虚数单位),就称f将点
为虚数单位),就称f将点 “f对应”到点
“f对应”到点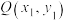 .例如
.例如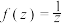 将点
将点 “f对应”到点
“f对应”到点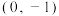 .
.
(1)若 点
点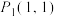 “f对应”到点
“f对应”到点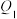 ,点
,点 “f对应”到点
“f对应”到点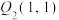 ,求点
,求点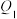 、
、 的坐标;
的坐标;
(2)设常数 ,
,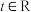 ,若直线l:
,若直线l: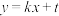 ,
,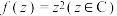 ,是否存在一个有序实数对
,是否存在一个有序实数对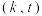 ,使得直线l上的任意一点
,使得直线l上的任意一点 “对应”到点
“对应”到点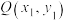 后,点Q仍在直线
后,点Q仍在直线 上?若存在,试求出所有的有序实数对
上?若存在,试求出所有的有序实数对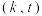 ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)设常数 ,
,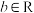 ,集合
,集合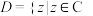 且
且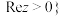 和
和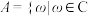 且
且 ,若
,若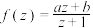 满足:①对于集合D中的任意一个元素z,都有
满足:①对于集合D中的任意一个元素z,都有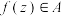 ;②对于集合A中的任意一个元素
;②对于集合A中的任意一个元素 ,都存在集合D中的元素z使得
,都存在集合D中的元素z使得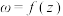 .请写出满足条件的一个有序实数对
.请写出满足条件的一个有序实数对 ,并论证此时的
,并论证此时的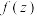 满足条件.
满足条件.
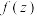 是一个关于复数z的表达式,若
是一个关于复数z的表达式,若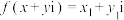 (其中x,y,
(其中x,y, ,
,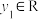

 为虚数单位),就称f将点
为虚数单位),就称f将点 “f对应”到点
“f对应”到点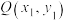 .例如
.例如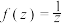 将点
将点 “f对应”到点
“f对应”到点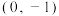 .
.(1)若
 点
点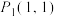 “f对应”到点
“f对应”到点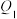 ,点
,点 “f对应”到点
“f对应”到点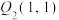 ,求点
,求点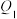 、
、 的坐标;
的坐标;(2)设常数
 ,
,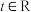 ,若直线l:
,若直线l: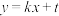 ,
,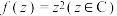 ,是否存在一个有序实数对
,是否存在一个有序实数对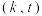 ,使得直线l上的任意一点
,使得直线l上的任意一点 “对应”到点
“对应”到点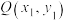 后,点Q仍在直线
后,点Q仍在直线 上?若存在,试求出所有的有序实数对
上?若存在,试求出所有的有序实数对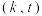 ;若不存在,请说明理由;
;若不存在,请说明理由;(3)设常数
 ,
,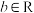 ,集合
,集合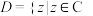 且
且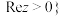 和
和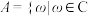 且
且 ,若
,若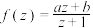 满足:①对于集合D中的任意一个元素z,都有
满足:①对于集合D中的任意一个元素z,都有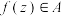 ;②对于集合A中的任意一个元素
;②对于集合A中的任意一个元素 ,都存在集合D中的元素z使得
,都存在集合D中的元素z使得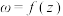 .请写出满足条件的一个有序实数对
.请写出满足条件的一个有序实数对 ,并论证此时的
,并论证此时的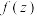 满足条件.
满足条件.
您最近半年使用:0次
2023-07-05更新
|
638次组卷
|
5卷引用:上海市控江中学2022-2023学年高一下学期期末数学试题
上海市控江中学2022-2023学年高一下学期期末数学试题上海市静安区回民中学2024届高三上学期12月阶段性测试数学试题(已下线)专题01 条件开放型【练】【通用版】湖南省邵阳市第二中学2024届高三下学期入学测试数学试题(已下线)高一下学期期中数学试卷(提高篇)-举一反三系列
名校
解题方法
9 . 已知常数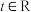 ,集合
,集合 ,
,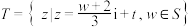 ,若
,若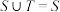 ,则t的取值范围是
,则t的取值范围是____________ .
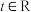 ,集合
,集合 ,
,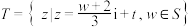 ,若
,若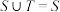 ,则t的取值范围是
,则t的取值范围是
您最近半年使用:0次
10 . 利用平面向量的坐标表示,可以把平面向量的概念推广为坐标为复数的“复向量”,即可将有序复数对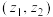 (其中
(其中 )视为一个向量,记作
)视为一个向量,记作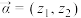 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量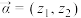 ,
,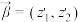 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足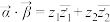 ,复向量
,复向量 的模定义为
的模定义为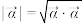 .
.
(1)设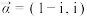 ,
, ,
, 为虚数单位,求复向量
为虚数单位,求复向量 、
、 的模;
的模;
(2)设 、
、 是两个复向量,
是两个复向量,
①已知对于任意两个平面向量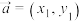 ,
,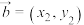 ,(其中
,(其中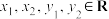 ),
), 成立,证明:对于复向量
成立,证明:对于复向量 、
、 ,
, 也成立;
也成立;
②当 时,称复向量
时,称复向量 与
与 平行.若复向量
平行.若复向量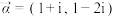 与
与 平行(其中
平行(其中 为虚数单位,
为虚数单位,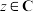 ),求复数
),求复数 .
.
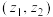 (其中
(其中 )视为一个向量,记作
)视为一个向量,记作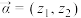 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量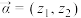 ,
,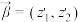 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足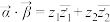 ,复向量
,复向量 的模定义为
的模定义为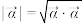 .
.(1)设
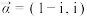 ,
, ,
, 为虚数单位,求复向量
为虚数单位,求复向量 、
、 的模;
的模;(2)设
 、
、 是两个复向量,
是两个复向量,①已知对于任意两个平面向量
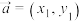 ,
,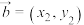 ,(其中
,(其中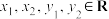 ),
), 成立,证明:对于复向量
成立,证明:对于复向量 、
、 ,
, 也成立;
也成立;②当
 时,称复向量
时,称复向量 与
与 平行.若复向量
平行.若复向量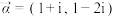 与
与 平行(其中
平行(其中 为虚数单位,
为虚数单位,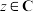 ),求复数
),求复数 .
.
您最近半年使用:0次



