名校
1 . 下列说法中不正确的有_______ .
①集合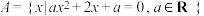 ,若集合
,若集合 有且仅有
有且仅有 个子集,则
个子集,则 的值为
的值为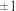 ;
;
②若 、
、 、
、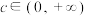 ,则
,则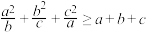 ;
;
③设 、
、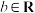 ,则“
,则“ ”是“
”是“ ”的充要条件;
”的充要条件;
④若实数 、
、 满足
满足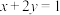 ,则
,则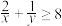 ;
;
⑤若 ,
, ,对应关系
,对应关系 ,
, 是
是 的函数.
的函数.
①集合
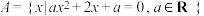 ,若集合
,若集合 有且仅有
有且仅有 个子集,则
个子集,则 的值为
的值为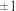 ;
;②若
 、
、 、
、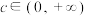 ,则
,则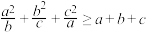 ;
;③设
 、
、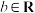 ,则“
,则“ ”是“
”是“ ”的充要条件;
”的充要条件;④若实数
 、
、 满足
满足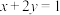 ,则
,则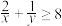 ;
;⑤若
 ,
, ,对应关系
,对应关系 ,
, 是
是 的函数.
的函数.
您最近一年使用:0次
2024-10-18更新
|
112次组卷
|
2卷引用:山西省太原市成成中学晋源校区2024-2025学年高一上学期10月月考数学试题
2 . 已知全集 ,集合
,集合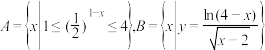
(1)求集合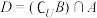 ;
;
(2)若集合 ,且
,且 ,求实数a的取值范围.
,求实数a的取值范围.
 ,集合
,集合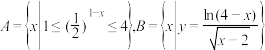
(1)求集合
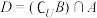 ;
;(2)若集合
 ,且
,且 ,求实数a的取值范围.
,求实数a的取值范围.
您最近一年使用:0次
名校
3 . 已知集合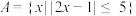 ,
, .
.
(1)若 ,求
,求 ;
;
(2)若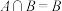 ,求
,求 的取值范围.
的取值范围.
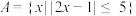 ,
, .
.(1)若
 ,求
,求 ;
;(2)若
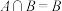 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
4 . 如图,在平面直角坐标系中,直线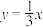 与双曲线
与双曲线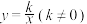 交于点
交于点 ,过点
,过点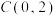 作
作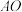 的平行线交双曲线于点
的平行线交双曲线于点 ,连接
,连接 并延长与
并延长与 轴交于点
轴交于点 ,则
,则 的值为
的值为______ .
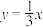 与双曲线
与双曲线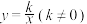 交于点
交于点 ,过点
,过点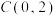 作
作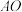 的平行线交双曲线于点
的平行线交双曲线于点 ,连接
,连接 并延长与
并延长与 轴交于点
轴交于点 ,则
,则 的值为
的值为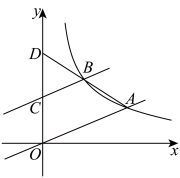
您最近一年使用:0次
2024-09-08更新
|
134次组卷
|
3卷引用:山西省太原市实验中学校2024-2025学年高一上学期开学考试数学试题
名校
5 . 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件,当每件商品降价多少元时,该商店每天有最大销售利润为多少元?
您最近一年使用:0次
2024-08-29更新
|
33次组卷
|
2卷引用:山西省太原市实验中学校2024-2025学年高一上学期开学考试数学试题
6 . 已知 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若 .
.
(1)求B;
(2)若 ,且
,且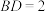 ,求
,求 的面积的最大值.
的面积的最大值.
 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若 .
.(1)求B;
(2)若
 ,且
,且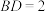 ,求
,求 的面积的最大值.
的面积的最大值.
您最近一年使用:0次
名校
7 . 已知向量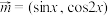 ,
,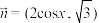 ,函数
,函数 .
.
(1)求函数 的解析式和图象的对称中心;
的解析式和图象的对称中心;
(2)若函数 的图象向左平移
的图象向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,且关于x的方程
的图象,且关于x的方程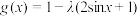 在
在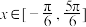 上有3个不同的解,求实数
上有3个不同的解,求实数 的取值范围.
的取值范围.
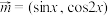 ,
,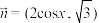 ,函数
,函数 .
.(1)求函数
 的解析式和图象的对称中心;
的解析式和图象的对称中心;(2)若函数
 的图象向左平移
的图象向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,且关于x的方程
的图象,且关于x的方程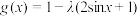 在
在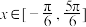 上有3个不同的解,求实数
上有3个不同的解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-17更新
|
691次组卷
|
4卷引用:山西省临汾市名校联考2023-2024学年高一下学期5月质量检测数学试题
名校
解题方法
8 . 已知 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,向量
,向量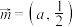 与
与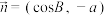 垂直.
垂直.
(1)求 ;
;
(2)若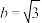 ,求
,求 的周长的取值范围.
的周长的取值范围.
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,向量
,向量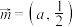 与
与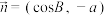 垂直.
垂直.(1)求
 ;
;(2)若
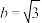 ,求
,求 的周长的取值范围.
的周长的取值范围.
您最近一年使用:0次
2024-05-14更新
|
762次组卷
|
2卷引用:山西省长治市上党区第一中学等校2023-2024学年高一下学期4月期中联考数学试题
9 . 定义非零向量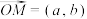 的“相伴函数”为
的“相伴函数”为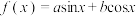 (
( ),向量
),向量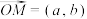 称为函数
称为函数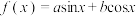 (
( )的“相伴向量”(其中O为坐标原点).
)的“相伴向量”(其中O为坐标原点).
(1)设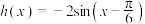 (
( ),写出函数
),写出函数 的相伴向量
的相伴向量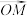 ;
;
(2)已知 的内角A,B,C的对边分别为a,b,c,记向量
的内角A,B,C的对边分别为a,b,c,记向量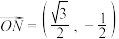 的相伴函数
的相伴函数 ,若
,若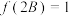 且
且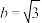 ,求
,求 的取值范围;
的取值范围;
(3)已知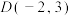 ,
, ,
, 为(2)中函数,
为(2)中函数,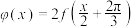 ,请问在
,请问在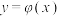 的图象上是否存在一点P,使得
的图象上是否存在一点P,使得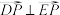 ?若存在,求出P点坐标;若不存在,说明理由.
?若存在,求出P点坐标;若不存在,说明理由.
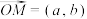 的“相伴函数”为
的“相伴函数”为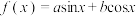 (
( ),向量
),向量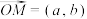 称为函数
称为函数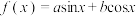 (
( )的“相伴向量”(其中O为坐标原点).
)的“相伴向量”(其中O为坐标原点).(1)设
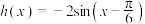 (
( ),写出函数
),写出函数 的相伴向量
的相伴向量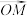 ;
;(2)已知
 的内角A,B,C的对边分别为a,b,c,记向量
的内角A,B,C的对边分别为a,b,c,记向量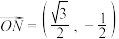 的相伴函数
的相伴函数 ,若
,若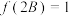 且
且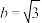 ,求
,求 的取值范围;
的取值范围;(3)已知
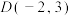 ,
, ,
, 为(2)中函数,
为(2)中函数,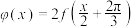 ,请问在
,请问在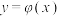 的图象上是否存在一点P,使得
的图象上是否存在一点P,使得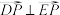 ?若存在,求出P点坐标;若不存在,说明理由.
?若存在,求出P点坐标;若不存在,说明理由.
您最近一年使用:0次
2024-04-03更新
|
750次组卷
|
3卷引用:山西省运城市盐湖区运城南风学校2023-2024学年高一下学期3月月考数学试题
山西省运城市盐湖区运城南风学校2023-2024学年高一下学期3月月考数学试题(已下线)专题01 第六章 平面向量-期末考点大串讲(人教A版2019必修第二册)黑龙江省齐齐哈尔市普高联谊校2023-2024学年高一下学期4月期中数学试题
名校
解题方法
10 . 求值:
(1)
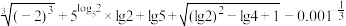
(2)
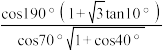
您最近一年使用:0次



