名校
解题方法
1 . 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上:以小斜幂乘大斜幂,减上,余四约之,为实:一为从隅,开平方得积可用公式 (其中
(其中 、
、 、
、 、
、 为三角形的三边和面积)表示.在
为三角形的三边和面积)表示.在 中,
中, 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,若
所对的边,若 ,且
,且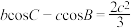 ,则
,则 面积的最大值为
面积的最大值为___________ .
 (其中
(其中 、
、 、
、 、
、 为三角形的三边和面积)表示.在
为三角形的三边和面积)表示.在 中,
中, 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,若
所对的边,若 ,且
,且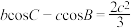 ,则
,则 面积的最大值为
面积的最大值为
您最近一年使用:0次
2021-03-26更新
|
2022次组卷
|
17卷引用:浙江省精诚联盟2020-2021学年高一下学期3月联考数学试题
浙江省精诚联盟2020-2021学年高一下学期3月联考数学试题(已下线)【新东方】双师160高一下(已下线)【新东方】双师166高一下(已下线)【新东方】在线数学145高一下(已下线)【新东方】高中数学20210513-005【2021】【高一下】(已下线)【新东方】【2021.5.19】【SX】【高三下】【高中数学】【SX00161】(已下线)期末测试卷01-2020-2021学年高一数学下学期期末专项复习(北师大版2019必修第二册)湖北省部分重点高中2020-2021学年高一下学期四月联考数学试题河北省沧州市肃宁县第一中学2020-2021学年高一下学期4月月考数学试题云南省玉溪第一中学2020-2021学年高一下学期期中考试数学试题江苏省淮安市郑梁梅高级中学等六校联盟2020-2021学年高一下学期第六次学情调查数学试题(已下线)期中全真模拟试卷(4)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)江苏省南通市启东中学2020-2021学年高一下学期第二次月考数学试题广东省东莞市第四高级中学2020-2021学年高一下学期4月段考数学试题(已下线)5.5 正余弦定理(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)2021年新高考浙江数学高考真题变式题11-16题江西省上高二中2022-2023学年高一下学期期末数学复习卷试题
20-21高三下·浙江·阶段练习
名校
2 . 已知锐角 中,
中,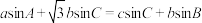 .
.
(1)求 ;
;
(2)求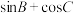 的取值范围.
的取值范围.
 中,
中,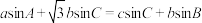 .
.(1)求
 ;
;(2)求
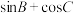 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 设 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若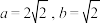 ,则角B可以是( )
,则角B可以是( )
 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若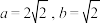 ,则角B可以是( )
,则角B可以是( )A. | B. | C. | D.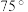 |
您最近一年使用:0次
2021-05-05更新
|
1759次组卷
|
9卷引用:浙江省宁波市咸祥中学2021-2022学年高一下学期期中数学试题
浙江省宁波市咸祥中学2021-2022学年高一下学期期中数学试题福建省漳州市2021届高三高考二模数学试题湖南省长沙市长郡中学2021届高三下学期保温卷二数学试题福建省漳州第一中学2020-2021学年高一下学期数学期末试题(已下线)5.5 正余弦定理(精讲)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)专题19 解三角形-2023届高考数学一轮复习精讲精练(新高考专用)广东省揭阳市揭西县河婆中学2022届高三下学期综合测试(二)数学试题福建省漳州第一中学2023届高三上学期第一次阶段考试数学试题福建省宁德第一中学2020-2021学年高一下学期第二次月考数学试题
4 . 已知 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且满足①
,且满足①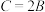 ;②
;② ;③
;③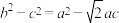 .
.
(1)从①②③中选取两个作为条件,证明另外一个成立;
(2)若 为线段
为线段 上一点,且
上一点,且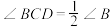 ,
,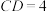 ,求
,求 的面积.
的面积.
 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且满足①
,且满足①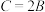 ;②
;② ;③
;③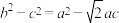 .
.(1)从①②③中选取两个作为条件,证明另外一个成立;
(2)若
 为线段
为线段 上一点,且
上一点,且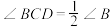 ,
,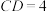 ,求
,求 的面积.
的面积.
您最近一年使用:0次
2022-01-16更新
|
1120次组卷
|
5卷引用:解密06 解三角形(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)
(已下线)解密06 解三角形(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)云南省昆明市2022届高三“三诊一模”市统测数学(理)试题河南省南阳市第一中学校2021-2022学年高三上学期第一次网上限时训练数学(理)试题江苏省木渎高级中学、苏苑高级中学2022届高三下学期联合适应性检测数学试题福建省莆田第八中学2023届高三上学期入学模拟考试数学试题(一)
解题方法
5 . 已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且满足
,且满足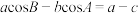 .
.
(1)求 ;
;
(2)若 为边
为边 的中点,求
的中点,求 的长.
的长.
 的内角
的内角 所对的边分别为
所对的边分别为 ,且满足
,且满足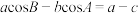 .
.(1)求
 ;
;(2)若
 为边
为边 的中点,求
的中点,求 的长.
的长.
您最近一年使用:0次
名校
解题方法
6 . 已知双曲线 左右焦点为
左右焦点为 ,过
,过 的直线与双曲线的右支交于
的直线与双曲线的右支交于 ,
, 两点,且
两点,且 ,若线段
,若线段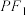 的中垂线过点
的中垂线过点 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 左右焦点为
左右焦点为 ,过
,过 的直线与双曲线的右支交于
的直线与双曲线的右支交于 ,
, 两点,且
两点,且 ,若线段
,若线段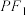 的中垂线过点
的中垂线过点 ,则双曲线的离心率为( )
,则双曲线的离心率为( )| A.3 | B.2 | C. | D. |
您最近一年使用:0次
名校
7 . 在△ABC中,角A,B,C的对边分别为a,b,c,其面积为S,且(c﹣a)(c+a)+abcosC= S.
S.
(1)求角A的大小;
(2)若4cosB•cosC=1,且a=2 ,求S的值.
,求S的值.
 S.
S.(1)求角A的大小;
(2)若4cosB•cosC=1,且a=2
 ,求S的值.
,求S的值.
您最近一年使用:0次
2021-06-20更新
|
1569次组卷
|
12卷引用:2021年秋季高三数学开学摸底考试卷01(浙江专用)
(已下线)2021年秋季高三数学开学摸底考试卷01(浙江专用)全国2021届高三数学模拟试题(样卷二)湖南省(全国卷)2021届高三高考数学模拟试题(样卷二)全国2021届高三高考数学模拟试题(样卷二)内蒙古赤峰二中2021-2022学年高三上学期第一次月考数学(理)试题(已下线)2020年高考浙江数学高考真题变式题17-22题2023年3月河北省普通高中学业水平合格性考试模拟(三)数学试题安徽省合肥市肥东县综合高中2022-2023学年高三下学期第一次模拟数学试题(已下线)专题07三角函数与解三角形(解答题)青海省西宁市六校联考2022-2023学年高三下学期开学考试数学(理)试题福建省福州市高新区第一中学(闽侯县第三中学)2024届高三上学期12月月考数学试题内蒙古呼伦贝尔市额尔古纳第一中学2022-2023学年高三上学期8月月考数学试题(理)
名校
解题方法
8 . 已知 满足
满足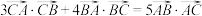 ,则
,则 的最小值为( )
的最小值为( )
 满足
满足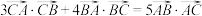 ,则
,则 的最小值为( )
的最小值为( )A. | B. | C. | D. |
您最近一年使用:0次
9 . 已知正三棱柱 的各棱长均为2,M,N分别为棱
的各棱长均为2,M,N分别为棱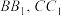 上的点.若平面
上的点.若平面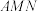 将三棱柱分为上、下体积相等的两部分,则
将三棱柱分为上、下体积相等的两部分,则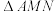 的面积的最小值为
的面积的最小值为
您最近一年使用:0次
12-13高三上·浙江台州·阶段练习
名校
解题方法
10 . 在锐角三角形 中,A、B、C的对边分别为a、b、c,
中,A、B、C的对边分别为a、b、c,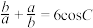 ,则
,则
______ .
 中,A、B、C的对边分别为a、b、c,
中,A、B、C的对边分别为a、b、c,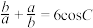 ,则
,则
您最近一年使用:0次
2021-09-25更新
|
1545次组卷
|
26卷引用:2012届浙江省台州市台州中学高三上学期第三次统练理科数学
(已下线)2012届浙江省台州市台州中学高三上学期第三次统练理科数学(已下线)2012-2013学年浙江北仑中学高一(7、8班)下期中考试数学试卷浙江省金华市曙光学校2019-2020学年高一下学期返校测试数学试题(已下线)2013届四川成都龙泉驿区5月高三押题试卷理科数学试卷(已下线)2014-2015学年河南郑州外国语学校高二上学期第一次月考理科数学卷2015-2016学年河北省唐山市一中高一3月月考数学试卷2015-2016学年河北省唐山一中高一3月月考数学试卷2016-2017学年山东鄄城县一中高二探究部月考二数学试卷河南省郑州市第一中学网校2017-2018学年高二上学期期中联考数学(理)试题(已下线)3.3 正弦定理 余弦定理与解三角形 [理]-《备战2020年高考精选考点专项突破题集》(已下线)3.3 正弦定理 余弦定理与解三角形 [文] -《备战2020年高考精选考点专项突破题集》上海市七宝中学2016-2017学年高一下学期期中数学试题上海市七宝中学2016-2017学年高二上学期开学考试数学试题(已下线)考点17 正余弦定理(练习)-2021年高考数学复习一轮复习笔记湖北省武汉市武昌实验中学2019-2020学年高一下学期期中数学试题(已下线)上海期末真题精选50题(小题压轴版)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)高中数学解题兵法 第四十六讲 等价转化法(已下线)第6章 三角(章节压轴题解题思路分析)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)(已下线)专题02解三角形-测案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题02解三角形-测案(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题07 盘点解三角形中的多边形与多元问题——备战2022年高考数学二轮复习常考点专题突破上海市建平中学2021-2022学年高一下学期3月月考数学试题四川省攀枝花市第十五中学校2021-2022学年高一下学期第一次月考数学试题黑龙江省哈尔滨市第一中学校2021-2022学年高三上学期期中考试数学(理科)试题河北师范大学附属中学2023-2024学年高二上学期开学考数学试题第十三届高一试题(A卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)



