名校
1 . 设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,下顶点为
,下顶点为 ,椭圆
,椭圆 的离心率是
的离心率是 ,
,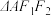 的面积是
的面积是 .
.
(1)求椭圆 的标准方程.
的标准方程.
(2)直线 与椭圆
与椭圆 交于
交于 ,
, 两点(异于
两点(异于 点),若直线
点),若直线 与直线
与直线 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,下顶点为
,下顶点为 ,椭圆
,椭圆 的离心率是
的离心率是 ,
,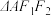 的面积是
的面积是 .
.(1)求椭圆
 的标准方程.
的标准方程.(2)直线
 与椭圆
与椭圆 交于
交于 ,
, 两点(异于
两点(异于 点),若直线
点),若直线 与直线
与直线 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
您最近一年使用:0次
2020-01-07更新
|
1048次组卷
|
13卷引用:甘肃省酒泉市2019-2020学年高二上学期期末数学(理)试题
甘肃省酒泉市2019-2020学年高二上学期期末数学(理)试题河南省创新发展联盟2019-2020学年高二上学期第三次联考数学(理)试题河南省创新发展联盟2019-2020学年高二上学期第三次联考数学(文)试题安徽省皖西南联盟2019-2020学年高二上学期期末数学(理)试题湖北省十堰市2019-2020学年高二上学期期末数学试题甘肃省白银市靖远县2019-2020学年高二上学期期末数学(理)试题广西玉林市第十一中学2019-2020学年高二数学(文)期末试题广东深圳龙岗区华中师范大学龙岗附属中学2020-2021学年高二下学期开学考试数学试题广东省佛山市南海区超盈实验中学2021-2022学年高二上学期第二次大测数学试题广西玉林市第十一中学2021-2022学年高二上学期期末模拟考试数学(理)试题广西玉林市第十一中学2021-2022学年高二上学期期末模拟考试数学(文)试题天津市第二十五中学2020年高三3月网络测试数学试题2020届天津二十五中高三高考模拟(3月份)数学试题
名校
2 . “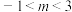 ”是“方程
”是“方程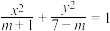 表示椭圆”的( )
表示椭圆”的( )
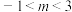 ”是“方程
”是“方程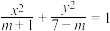 表示椭圆”的( )
表示椭圆”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2020-01-07更新
|
882次组卷
|
12卷引用:甘肃省酒泉市2019-2020学年高二上学期期末数学(理)试题
甘肃省酒泉市2019-2020学年高二上学期期末数学(理)试题甘肃省酒泉市2019-2020学年高二上学期期末数学(文)试题河南省创新发展联盟2019-2020学年高二上学期第三次联考数学(理)试题河南省创新发展联盟2019-2020学年高二上学期第三次联考数学(文)试题广东省2019-2020学年高二上学期期末数学试题湖北省十堰市2019-2020学年高二上学期期末数学试题甘肃省白银市靖远县2019-2020学年高二上学期期末数学(理)试题甘肃省白银市靖远县2019-2020学年高二上学期期末数学(文)试题江苏省南通市海安高级中学2023-2024学年高二上学期期中数学试题广东省湛江市2020-2021学年高二上学期期末数学试题(已下线)期末精确押题之单选题(45题)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)河北省邯郸一中2019-2020学年高三下学期第九次模拟数学试题
名校
解题方法
3 . 如图,椭圆 经过点
经过点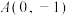 ,且离心率为
,且离心率为 .
.
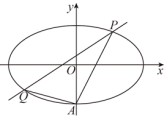
(1)求椭圆E的方程;
(2)若经过点 ,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
 经过点
经过点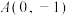 ,且离心率为
,且离心率为 .
.
(1)求椭圆E的方程;
(2)若经过点
 ,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
,且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为定值.
您最近一年使用:0次
2020-11-12更新
|
1803次组卷
|
26卷引用:甘肃省玉门一中2018-2019学年高二上学期期末考试数学(文)试题
甘肃省玉门一中2018-2019学年高二上学期期末考试数学(文)试题2015-2016学年陕西省西安市七十中高二上学期期末理科数学试卷2015-2016学年陕西省西安市七十中高二上学期期末文科数学试卷北京市北京师范大学附属中学2016-2017学年高二下学期期中考试数学(文)试题【市级联考】安徽省安庆市2018-2019学年高二第一学期期末教学质量调研监测文科数学试题【校级联考】湖北省孝感市联考协作体2018-2019学年高二下学期期中考试数学(文)试题【区级联考】2018-2019学年江西省赣州市十五县(市)高二(下)期中数学(文科)试题广西南宁市马山县金伦中学“4+ N”高中联合体2018-2019学年高二上学期期末数学(理)试题河北省正定县弘文中学2020-2021学年高二上学期9月月考数学试题重庆市渝北区松树桥中学2020-2021学年高二上学期11月月考数学试题北京市第四十三中学2020-2021学年高二12月月考数学试题江西省吉安县立中学2020-2021学年高二12月月考数学(文B)试题湖南省常德市石门县第六中学2020-2021学年高二上学期期末数学试题广东省实验中学越秀学校2020-2021学年高二上学期期中数学试题江西省兴国县第三中学2020-2021学年高二下学期第一次月考数学(文)试题吉林省汪清县汪清第四中学2021-2022学年高二上学期第二次阶段检测数学试题黑龙江省齐齐哈尔市第八中学校2023-2024学年高二上学期12月月考数学试题2016届山东省济南外国语学校高三上开学考试文科数学试卷人教A版高中数学 高三二轮 专题11 圆锥曲线中的定点、定值、最值与范围问题 测试【校级联考】湖北省武汉市部分市级示范高中2019届高三12月联考数学(理科)试题湖南师大附中2020届高三下学期月考(七)数学(文)试题安徽省亳州市利辛县阚疃金石中学2020-2021学年高三上学期第一次月考数学试题江苏省徐州市沛县2020-2021学年高三上学期第一次学情调研数学试题江西省九江市三中2019届高三上学期期中文数试题山西省大同市煤矿第四中学校2021届高三上学期期中数学(文)试题福建省厦门双十中学2021届高三12月月考数学试题
4 . 已知椭圆C: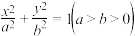 的左右焦点分别为
的左右焦点分别为 ,
, ,焦距为2,过
,焦距为2,过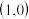 点作直线与椭圆相交于A,B两点,连接
点作直线与椭圆相交于A,B两点,连接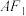 ,
,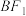 ,且
,且 的周长为
的周长为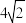 .
.
 求椭圆C的标准方程
求椭圆C的标准方程
 若
若 ,求直线AB的方程.
,求直线AB的方程.
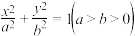 的左右焦点分别为
的左右焦点分别为 ,
, ,焦距为2,过
,焦距为2,过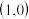 点作直线与椭圆相交于A,B两点,连接
点作直线与椭圆相交于A,B两点,连接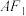 ,
,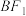 ,且
,且 的周长为
的周长为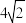 .
. 求椭圆C的标准方程
求椭圆C的标准方程 若
若 ,求直线AB的方程.
,求直线AB的方程.
您最近一年使用:0次
2019-03-17更新
|
476次组卷
|
3卷引用:甘肃省酒泉市玉门市2021-2022学年高二上学期期中数学(文)试题
13-14高三上·山西忻州·阶段练习
名校
解题方法
5 . 已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆 的方程;
的方程;
(2)设直线 经过点
经过点 ,且与椭圆
,且与椭圆 交于
交于 ,
, 两点,若
两点,若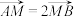 ,求直线
,求直线 的方程.
的方程.
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆
 的方程;
的方程;(2)设直线
 经过点
经过点 ,且与椭圆
,且与椭圆 交于
交于 ,
, 两点,若
两点,若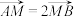 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2019-01-30更新
|
907次组卷
|
13卷引用:甘肃省酒泉市瓜州县2017-2018学年高二上学期期末数学(文)试题
甘肃省酒泉市瓜州县2017-2018学年高二上学期期末数学(文)试题人教A版(2019) 选择性必修第一册 必杀技 模块综合测试云南省弥勒市第一中学2019-2020学年高二下学期第三次月考数学(文)试题苏教版(2019) 选修第一册 必杀技 模块综合测试人教A版(2019) 选修第一册 实战演练 第三章 课时练习23 直线与椭圆的位置关系内蒙古赤峰市红山区2021-2022学年高二上学期质量检测数学(理科)试题(已下线)2014届山西忻州一中等四校高三上学期第二次联考理科数学试卷2015届北京市石景山区高三上学期期末考试文科数学试卷河南省周口市中英文学校2018届高三上学期开学摸底考试数学试题(已下线)专题54 圆锥曲线大题解题模板-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题54 圆锥曲线大题解题模板-2021年高考一轮数学(理)单元复习一遍过(已下线)专题51 圆锥曲线大题解题模板-2021年高考一轮数学(文)单元复习一遍过山东省青岛市青岛第十七中学2020-2021学年高三上学期期中数学试题



