1 . 如图,抛物线 过点
过点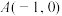 和点
和点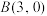 ,与
,与 轴交于点
轴交于点 ,抛物线的对称轴
,抛物线的对称轴 交
交 轴于点
轴于点 ,交抛物线于点
,交抛物线于点 .
.
(1)求抛物线的表达式及 点的坐标;
点的坐标;
(2)点 是直线
是直线 上的点,若
上的点,若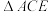 的面积与
的面积与 的面积相等,求点
的面积相等,求点 的坐标;
的坐标;
(3)点 在第四象限,且为抛物线上的点,若四边形
在第四象限,且为抛物线上的点,若四边形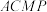 是梯形,求点
是梯形,求点 的坐标.
的坐标.
 过点
过点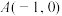 和点
和点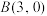 ,与
,与 轴交于点
轴交于点 ,抛物线的对称轴
,抛物线的对称轴 交
交 轴于点
轴于点 ,交抛物线于点
,交抛物线于点 .
.
(1)求抛物线的表达式及
 点的坐标;
点的坐标;(2)点
 是直线
是直线 上的点,若
上的点,若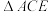 的面积与
的面积与 的面积相等,求点
的面积相等,求点 的坐标;
的坐标;(3)点
 在第四象限,且为抛物线上的点,若四边形
在第四象限,且为抛物线上的点,若四边形 是梯形,求点
是梯形,求点 的坐标.
的坐标.
您最近一年使用:0次
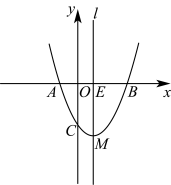
2 . 如图,在平面直角坐标系中,抛物线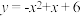 与直线
与直线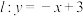 交于A、C两点,直线l与y轴交于点B,抛物线上的动点D在直线l的上方.
交于A、C两点,直线l与y轴交于点B,抛物线上的动点D在直线l的上方.

(1)请直接写出点A、点C的坐标;
(2)连接 、
、 ,当三角形
,当三角形 的面积最大时,求点D的坐标?
的面积最大时,求点D的坐标?
(3)连接 、
、 ,当三角形
,当三角形 以
以 边为直角边时,求点D的坐标?
边为直角边时,求点D的坐标?
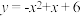 与直线
与直线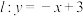 交于A、C两点,直线l与y轴交于点B,抛物线上的动点D在直线l的上方.
交于A、C两点,直线l与y轴交于点B,抛物线上的动点D在直线l的上方.
(1)请直接写出点A、点C的坐标;
(2)连接
 、
、 ,当三角形
,当三角形 的面积最大时,求点D的坐标?
的面积最大时,求点D的坐标?(3)连接
 、
、 ,当三角形
,当三角形 以
以 边为直角边时,求点D的坐标?
边为直角边时,求点D的坐标?
您最近一年使用:0次
3 . 如图,在直角坐标系中,二次函数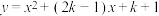 的图像与
的图像与 轴相交于
轴相交于 两点.
两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴和顶点坐标;
(3)在这条抛物线的图像上是否存在一点 ,使
,使 的面积等于6,若存在,请求出点
的面积等于6,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
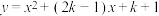 的图像与
的图像与 轴相交于
轴相交于 两点.
两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴和顶点坐标;
(3)在这条抛物线的图像上是否存在一点
 ,使
,使 的面积等于6,若存在,请求出点
的面积等于6,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
名校
4 . 已知抛物线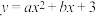 的顶点坐标为
的顶点坐标为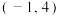 ,与x轴交于点A和点B,与y轴交于点C,点P为第二象限内抛物线上的动点.
,与x轴交于点A和点B,与y轴交于点C,点P为第二象限内抛物线上的动点.
(2)如图1,连接 交
交 于点D,当
于点D,当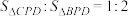 时,请求出点D的坐标;
时,请求出点D的坐标;
(3)如图2,点E的坐标为 ,点G为x轴负半轴上的一点,
,点G为x轴负半轴上的一点,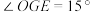 ,连接
,连接 ,若
,若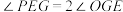 ,请求出点P的坐标;
,请求出点P的坐标;
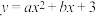 的顶点坐标为
的顶点坐标为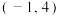 ,与x轴交于点A和点B,与y轴交于点C,点P为第二象限内抛物线上的动点.
,与x轴交于点A和点B,与y轴交于点C,点P为第二象限内抛物线上的动点.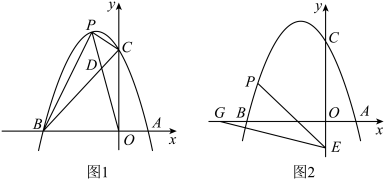
(2)如图1,连接
 交
交 于点D,当
于点D,当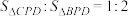 时,请求出点D的坐标;
时,请求出点D的坐标;(3)如图2,点E的坐标为
 ,点G为x轴负半轴上的一点,
,点G为x轴负半轴上的一点,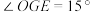 ,连接
,连接 ,若
,若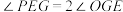 ,请求出点P的坐标;
,请求出点P的坐标;
您最近一年使用:0次
2024-03-02更新
|
605次组卷
|
7卷引用:云南省文山壮族苗族自治州文山市2023-2024学年九年级下学期3月月考数学试题
云南省文山壮族苗族自治州文山市2023-2024学年九年级下学期3月月考数学试题辽宁省鞍山市千山区2023-2024学年九年级上学期12月月考数学试题(已下线)专题04 二次函数 (1大易错点分析+20个易错点+易错题通关)-备战2024年中考数学考试易错题(江苏专用)2024学年重庆市求精中学校九年级下学期二调模拟考试数学模拟预测题(已下线)专题04 二次函数与几何综合-2024年中考数学二轮热点题型归纳与变式演练(江苏专用)2024年山东省菏泽市单县中考三模数学试题广东省佛山市南海区桂城街道文翰中学2023-2024学年九年级下学期6月月考数学试题
名校
5 . 如图,抛物线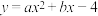 与
与 轴交于
轴交于 、
、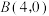 两点,与
两点,与 轴交于点
轴交于点 .
.
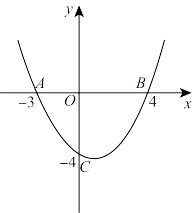
(1)求抛物线解析式;
(2)点 是抛物线对称轴上的一个动点,连接
是抛物线对称轴上的一个动点,连接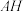 、
、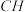 ,求出
,求出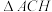 周长的最小值时点
周长的最小值时点 的坐标;
的坐标;
(3)若点 是第四象限抛物线上的动点,求
是第四象限抛物线上的动点,求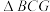 面积的最大值以及此时点
面积的最大值以及此时点 的坐标;
的坐标;
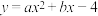 与
与 轴交于
轴交于 、
、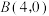 两点,与
两点,与 轴交于点
轴交于点 .
.
(1)求抛物线解析式;
(2)点
 是抛物线对称轴上的一个动点,连接
是抛物线对称轴上的一个动点,连接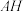 、
、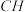 ,求出
,求出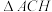 周长的最小值时点
周长的最小值时点 的坐标;
的坐标;(3)若点
 是第四象限抛物线上的动点,求
是第四象限抛物线上的动点,求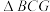 面积的最大值以及此时点
面积的最大值以及此时点 的坐标;
的坐标;
您最近一年使用:0次
6 . 如图,在边长为 的正方形
的正方形 中,点
中,点 ,
, ,
, ,
, 分别从点
分别从点 ,
, ,
, ,
, 同时出发,均以
同时出发,均以 的速度向点
的速度向点 ,
, ,
, ,
, 匀速运动,当点
匀速运动,当点 到达点
到达点 时,四个点同时停止运动,在运动过程中,当运动时间为
时,四个点同时停止运动,在运动过程中,当运动时间为________  时,四边形
时,四边形 ,的面积最小,其最小值是
,的面积最小,其最小值是________  .
.
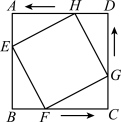
 的正方形
的正方形 中,点
中,点 ,
, ,
, ,
, 分别从点
分别从点 ,
, ,
, ,
, 同时出发,均以
同时出发,均以 的速度向点
的速度向点 ,
, ,
, ,
, 匀速运动,当点
匀速运动,当点 到达点
到达点 时,四个点同时停止运动,在运动过程中,当运动时间为
时,四个点同时停止运动,在运动过程中,当运动时间为 时,四边形
时,四边形 ,的面积最小,其最小值是
,的面积最小,其最小值是 .
.
您最近一年使用:0次
名校
7 . 如图所示,在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图象与x轴交于点
的图象与x轴交于点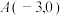 ,与y轴交于点B.
,与y轴交于点B.
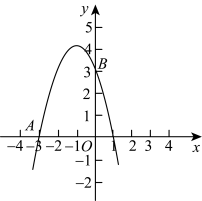
(1)求该函数的表达式及顶点坐标;
(2)将该二次函数图象在点A,B之间的部分(含A,B两点)记为图象W,点Q在图象W上,连接QA,QB,求 面积的最大值;
面积的最大值;
(3)点P(m,n)在该二次函数图象上,当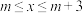 时,该二次函数有最大值2,请根据图象求出m的值;
时,该二次函数有最大值2,请根据图象求出m的值;
 中,已知二次函数
中,已知二次函数 的图象与x轴交于点
的图象与x轴交于点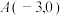 ,与y轴交于点B.
,与y轴交于点B.
(1)求该函数的表达式及顶点坐标;
(2)将该二次函数图象在点A,B之间的部分(含A,B两点)记为图象W,点Q在图象W上,连接QA,QB,求
 面积的最大值;
面积的最大值;(3)点P(m,n)在该二次函数图象上,当
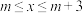 时,该二次函数有最大值2,请根据图象求出m的值;
时,该二次函数有最大值2,请根据图象求出m的值;
您最近一年使用:0次
名校
8 . 如图,抛物线 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在点
在点 的左侧),且点
的左侧),且点 为
为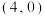 ,与
,与 轴交于点
轴交于点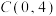 ,直线
,直线 经过
经过 ,
, 两点,点
两点,点 是第一象限内抛物线上的一个动点,连接
是第一象限内抛物线上的一个动点,连接 ,
, .
.
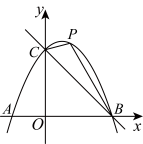
(1)求抛物线的函数表达式;
(2)直线 的解析式记为
的解析式记为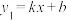 ,当
,当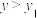 时,直接写出
时,直接写出 的取值范围;
的取值范围;
(3)设点 的横坐标为
的横坐标为 ,四边形
,四边形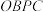 的面积为
的面积为 ,求
,求 的最大值并求出此时点
的最大值并求出此时点 的坐标.
的坐标.
 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在点
在点 的左侧),且点
的左侧),且点 为
为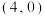 ,与
,与 轴交于点
轴交于点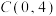 ,直线
,直线 经过
经过 ,
, 两点,点
两点,点 是第一象限内抛物线上的一个动点,连接
是第一象限内抛物线上的一个动点,连接 ,
, .
.
(1)求抛物线的函数表达式;
(2)直线
 的解析式记为
的解析式记为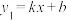 ,当
,当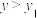 时,直接写出
时,直接写出 的取值范围;
的取值范围;(3)设点
 的横坐标为
的横坐标为 ,四边形
,四边形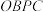 的面积为
的面积为 ,求
,求 的最大值并求出此时点
的最大值并求出此时点 的坐标.
的坐标.
您最近一年使用:0次
名校
9 . 如图,抛物线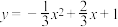 交
交 轴于A,B两点,交
轴于A,B两点,交 轴于点
轴于点 ,
, 是第一象限内抛物线上的一个动点.
是第一象限内抛物线上的一个动点.
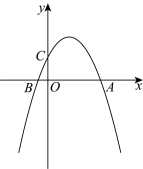
(1)求点A,B,C的坐标;
(2)求 面积的最大值;
面积的最大值;
(3)将 绕点
绕点 顺时针旋转
顺时针旋转 后,点
后,点 落在点
落在点 的位置,将抛物线沿
的位置,将抛物线沿 轴平移后经过点
轴平移后经过点 ,求平移后所得抛物线的解析式.
,求平移后所得抛物线的解析式.
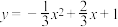 交
交 轴于A,B两点,交
轴于A,B两点,交 轴于点
轴于点 ,
, 是第一象限内抛物线上的一个动点.
是第一象限内抛物线上的一个动点.
(1)求点A,B,C的坐标;
(2)求
 面积的最大值;
面积的最大值;(3)将
 绕点
绕点 顺时针旋转
顺时针旋转 后,点
后,点 落在点
落在点 的位置,将抛物线沿
的位置,将抛物线沿 轴平移后经过点
轴平移后经过点 ,求平移后所得抛物线的解析式.
,求平移后所得抛物线的解析式.
您最近一年使用:0次
2023-11-03更新
|
92次组卷
|
2卷引用:云南省昆明市呈贡区第三中学2023-2024学年九年级上学期期中数学试题
名校
10 . 如图所示,在平面直角坐标系中,抛物线经过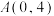 ,
,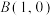 ,
,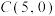 .
.
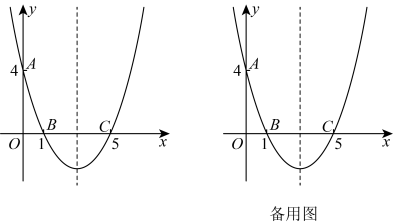
(1)求抛物线的解析式;
(2)该抛物线上有一点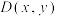
 不与点
不与点 、
、 、
、 重合
重合 ,使得
,使得 ,求点
,求点 的坐标;
的坐标;
(3)点 是线段
是线段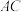 上的动点
上的动点 不与点
不与点 、点
、点 重合
重合 ,过点
,过点 作
作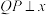 轴交抛物线于点
轴交抛物线于点 ,求线段
,求线段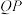 的最大值及此时
的最大值及此时 点的坐标.
点的坐标.
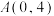 ,
,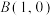 ,
,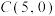 .
.
(1)求抛物线的解析式;
(2)该抛物线上有一点
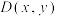
 不与点
不与点 、
、 、
、 重合
重合 ,使得
,使得 ,求点
,求点 的坐标;
的坐标;(3)点
 是线段
是线段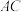 上的动点
上的动点 不与点
不与点 、点
、点 重合
重合 ,过点
,过点 作
作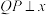 轴交抛物线于点
轴交抛物线于点 ,求线段
,求线段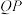 的最大值及此时
的最大值及此时 点的坐标.
点的坐标.
您最近一年使用:0次



