2023高三·全国·专题练习
解题方法
1 . 设M为部分正整数组成的集合,数列 的首项
的首项 ,前n项和为
,前n项和为 ,已知对任意整数k属于M,当
,已知对任意整数k属于M,当 时,
时,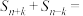
 都成立.设
都成立.设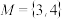 ,求数列
,求数列 的通项公式.
的通项公式.
 的首项
的首项 ,前n项和为
,前n项和为 ,已知对任意整数k属于M,当
,已知对任意整数k属于M,当 时,
时,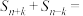
 都成立.设
都成立.设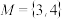 ,求数列
,求数列 的通项公式.
的通项公式.
您最近一年使用:0次
2023高三·全国·专题练习
解题方法
2 . 在数列 中,已知
中,已知 ,
, ,求通项公式
,求通项公式 .
.
 中,已知
中,已知 ,
, ,求通项公式
,求通项公式 .
.
您最近一年使用:0次
3 . 在数列 中,已知
中,已知 ,
,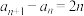 ,求通项公式
,求通项公式 .
.
 中,已知
中,已知 ,
,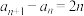 ,求通项公式
,求通项公式 .
.
您最近一年使用:0次
4 . 已知正项等比数列 和数列
和数列 ,满足
,满足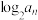 是
是 和
和 的等差中项,
的等差中项, .
.
(1)证明:数列 是等差数列,
是等差数列,
(2)若数列 的前
的前 项积
项积 满足
满足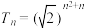 ,记
,记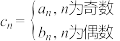 ,求数列
,求数列 的前20项和.
的前20项和.
 和数列
和数列 ,满足
,满足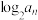 是
是 和
和 的等差中项,
的等差中项, .
.(1)证明:数列
 是等差数列,
是等差数列,(2)若数列
 的前
的前 项积
项积 满足
满足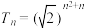 ,记
,记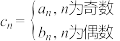 ,求数列
,求数列 的前20项和.
的前20项和.
您最近一年使用:0次
5 . 已知等差数列 的前n项和为
的前n项和为 ,且
,且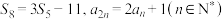 .
.
(1)求 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前n项和
的前n项和 .
.
 的前n项和为
的前n项和为 ,且
,且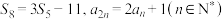 .
.(1)求
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列 的前n项和
的前n项和 .
.
您最近一年使用:0次
22-23高二下·全国·课后作业
解题方法
6 . 在等比数列 中:
中:
(1)若它的前三项分别为5, ,45,求
,45,求 ;
;
(2)若 =2,
=2, =8,求
=8,求 .
.
 中:
中:(1)若它的前三项分别为5,
 ,45,求
,45,求 ;
;(2)若
 =2,
=2, =8,求
=8,求 .
.
您最近一年使用:0次
解题方法
7 . 设数列 的前n项和为
的前n项和为 ,且满足
,且满足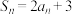 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:数列 中的任意不同的三项均不能构成等差数列.
中的任意不同的三项均不能构成等差数列.
 的前n项和为
的前n项和为 ,且满足
,且满足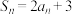 .
.(1)求数列
 的通项公式;
的通项公式;(2)证明:数列
 中的任意不同的三项均不能构成等差数列.
中的任意不同的三项均不能构成等差数列.
您最近一年使用:0次
8 . 已知数列 和
和 满足:
满足: ,
, ,
,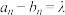 (
( 为常数,且
为常数,且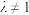 ).
).
(1)证明:数列 是等比数列;
是等比数列;
(2)若当 和
和 时,数列
时,数列 的前n项和
的前n项和 取得最大值,求
取得最大值,求 的表达式.
的表达式.
 和
和 满足:
满足: ,
, ,
,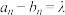 (
( 为常数,且
为常数,且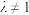 ).
).(1)证明:数列
 是等比数列;
是等比数列;(2)若当
 和
和 时,数列
时,数列 的前n项和
的前n项和 取得最大值,求
取得最大值,求 的表达式.
的表达式.
您最近一年使用:0次
2023-05-21更新
|
1357次组卷
|
5卷引用:海南省2023届高三学业水平诊断(五)数学试题
9 . 若数列 的首项为1,且
的首项为1,且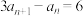 .
.
(1)求证: 是等比数列;
是等比数列;
(2)求 的前n项和
的前n项和 .
.
 的首项为1,且
的首项为1,且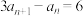 .
.(1)求证:
 是等比数列;
是等比数列;(2)求
 的前n项和
的前n项和 .
.
您最近一年使用:0次
10 . 已知 为数列
为数列 的前
的前 项和,满足
项和,满足 ,
, ,
,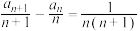 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前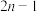 项和
项和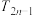 ,
,
 为数列
为数列 的前
的前 项和,满足
项和,满足 ,
, ,
,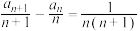 ,
,(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前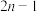 项和
项和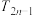 ,
,
您最近一年使用:0次



