解题方法
1 . 已知椭圆C: 的右顶点为
的右顶点为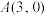 ,离心率为
,离心率为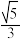 ,过点
,过点 的直线l与C交于M,N两点.
的直线l与C交于M,N两点.
(1)若C的上顶点为B,直线BM,BN的斜率分别为 ,
, ,求
,求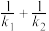 的值;
的值;
(2)过点M且垂直于x轴的直线交直线AN于点Q,证明:线段MQ的中点在定直线上.
 的右顶点为
的右顶点为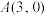 ,离心率为
,离心率为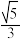 ,过点
,过点 的直线l与C交于M,N两点.
的直线l与C交于M,N两点.(1)若C的上顶点为B,直线BM,BN的斜率分别为
 ,
, ,求
,求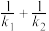 的值;
的值;(2)过点M且垂直于x轴的直线交直线AN于点Q,证明:线段MQ的中点在定直线上.
您最近一年使用:0次
今日更新
|
7次组卷
|
2卷引用:陕西省铜川市王益中学2024届高三下学期高考猜题信息卷(二)文科数学试题
名校
解题方法
2 . 已知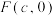 是椭圆
是椭圆 的右焦点,以坐标原点
的右焦点,以坐标原点 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过
,过 垂直于
垂直于 轴的直线与圆
轴的直线与圆 交于
交于 两点,过点A作圆
两点,过点A作圆 的切线交
的切线交 轴于点
轴于点 .若直线
.若直线 过点
过点 且垂直于
且垂直于 轴,则直线
轴,则直线 的方程为
的方程为______ ;若 ,则椭圆的离心率等于
,则椭圆的离心率等于______ .
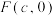 是椭圆
是椭圆 的右焦点,以坐标原点
的右焦点,以坐标原点 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过
,过 垂直于
垂直于 轴的直线与圆
轴的直线与圆 交于
交于 两点,过点A作圆
两点,过点A作圆 的切线交
的切线交 轴于点
轴于点 .若直线
.若直线 过点
过点 且垂直于
且垂直于 轴,则直线
轴,则直线 的方程为
的方程为 ,则椭圆的离心率等于
,则椭圆的离心率等于
您最近一年使用:0次
解题方法
3 . 油纸伞是中国传统工艺品,至今已有1000多年的历史.将油纸伞撑开后摆放在户外场地上,如图所示,该伞的伞沿是一个半径为 的圆,圆心到伞柄底端距离为
的圆,圆心到伞柄底端距离为 ,阳光照射油纸伞在地面形成了一个椭圆形影子(某时刻,阳光与地面夹角为
,阳光照射油纸伞在地面形成了一个椭圆形影子(某时刻,阳光与地面夹角为 ),若伞柄底端正好位于该椭圆的焦点位置,则该椭圆的离心率为( )
),若伞柄底端正好位于该椭圆的焦点位置,则该椭圆的离心率为( )
 的圆,圆心到伞柄底端距离为
的圆,圆心到伞柄底端距离为 ,阳光照射油纸伞在地面形成了一个椭圆形影子(某时刻,阳光与地面夹角为
,阳光照射油纸伞在地面形成了一个椭圆形影子(某时刻,阳光与地面夹角为 ),若伞柄底端正好位于该椭圆的焦点位置,则该椭圆的离心率为( )
),若伞柄底端正好位于该椭圆的焦点位置,则该椭圆的离心率为( )
A. | B. | C.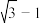 | D. |
您最近一年使用:0次
解题方法
4 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,左、右顶点分别为
,左、右顶点分别为 ,
, 是
是 上异于
上异于 的一个动点.若
的一个动点.若 ,则下列说法正确的有( )
,则下列说法正确的有( )
 的左、右焦点分别为
的左、右焦点分别为 ,左、右顶点分别为
,左、右顶点分别为 ,
, 是
是 上异于
上异于 的一个动点.若
的一个动点.若 ,则下列说法正确的有( )
,则下列说法正确的有( )A.椭圆 的离心率为 的离心率为 |
B.若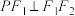 ,则 ,则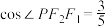 |
C.直线 的斜率与直线 的斜率与直线 的斜率之积等于 的斜率之积等于 |
D.符合条件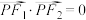 的点 的点 有且仅有2个 有且仅有2个 |
您最近一年使用:0次
解题方法
5 . 已知点 是椭圆
是椭圆 上的一点,左、右焦点分别为点
上的一点,左、右焦点分别为点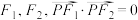 ,点
,点 在
在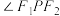 的平分线上,
的平分线上, 为坐标原点,
为坐标原点,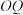

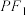 且
且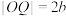 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
 是椭圆
是椭圆 上的一点,左、右焦点分别为点
上的一点,左、右焦点分别为点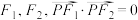 ,点
,点 在
在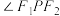 的平分线上,
的平分线上, 为坐标原点,
为坐标原点,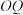

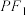 且
且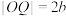 ,则椭圆的离心率为( )
,则椭圆的离心率为( )A.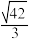 | B.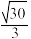 | C.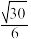 | D. |
您最近一年使用:0次
解题方法
6 . 已知双曲线 的顶点为椭圆
的顶点为椭圆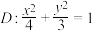 的焦点,
的焦点, 的离心率与
的离心率与 的离心率之积为1,则
的离心率之积为1,则 的方程为( )
的方程为( )
 的顶点为椭圆
的顶点为椭圆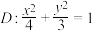 的焦点,
的焦点, 的离心率与
的离心率与 的离心率之积为1,则
的离心率之积为1,则 的方程为( )
的方程为( )A.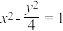 | B.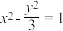 | C.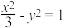 | D.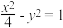 |
您最近一年使用:0次
7日内更新
|
248次组卷
|
2卷引用:河南省商丘市部分学校2023-2024学年高二下学期期末考试数学试卷
名校
解题方法
7 . 已知 ,
, 是椭圆C:
是椭圆C: 的两个焦点,
的两个焦点,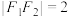 ,
,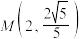 为C上一点.
为C上一点.
(1)求椭圆C的标准方程;
(2)若P为C上一点,且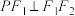 ,求
,求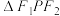 的面积.
的面积.
 ,
, 是椭圆C:
是椭圆C: 的两个焦点,
的两个焦点,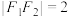 ,
,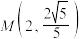 为C上一点.
为C上一点.(1)求椭圆C的标准方程;
(2)若P为C上一点,且
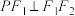 ,求
,求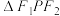 的面积.
的面积.
您最近一年使用:0次
解题方法
8 . 已知 为坐标原点,椭圆
为坐标原点,椭圆 :
: (
( )的右焦点为
)的右焦点为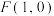 ,点
,点 在
在 上,且
上,且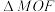 为等边三角形,则
为等边三角形,则 的离心率为
的离心率为______ .
 为坐标原点,椭圆
为坐标原点,椭圆 :
: (
( )的右焦点为
)的右焦点为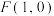 ,点
,点 在
在 上,且
上,且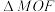 为等边三角形,则
为等边三角形,则 的离心率为
的离心率为
您最近一年使用:0次
9 . 设 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 于
于 两点,且
两点,且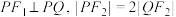 ,则椭圆
,则椭圆 的离心率为
的离心率为______ .
 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 于
于 两点,且
两点,且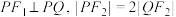 ,则椭圆
,则椭圆 的离心率为
的离心率为
您最近一年使用:0次
名校
解题方法
10 . 关于椭圆有如下结论:“过椭圆 上一点
上一点 作该椭圆的切线,切线方程为
作该椭圆的切线,切线方程为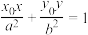 .”设椭圆
.”设椭圆 :
: 的左焦点为F,右顶点为A,过F且垂直于x轴的直线与C的一个交点为M,过M作椭圆的切线
的左焦点为F,右顶点为A,过F且垂直于x轴的直线与C的一个交点为M,过M作椭圆的切线 ,若切线
,若切线 与直线
与直线 的倾斜角互补,则C的离心率为( )
的倾斜角互补,则C的离心率为( )
 上一点
上一点 作该椭圆的切线,切线方程为
作该椭圆的切线,切线方程为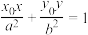 .”设椭圆
.”设椭圆 :
: 的左焦点为F,右顶点为A,过F且垂直于x轴的直线与C的一个交点为M,过M作椭圆的切线
的左焦点为F,右顶点为A,过F且垂直于x轴的直线与C的一个交点为M,过M作椭圆的切线 ,若切线
,若切线 与直线
与直线 的倾斜角互补,则C的离心率为( )
的倾斜角互补,则C的离心率为( )A. | B. | C. | D. |
您最近一年使用:0次



