1 . 设数列 满足
满足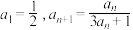 .
.
(1)证明: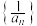 为等差数列;
为等差数列;
(2)若数列 的前
的前 项和为
项和为 ,证明:
,证明: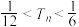 .
.
 满足
满足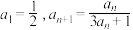 .
.(1)证明:
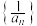 为等差数列;
为等差数列;(2)若数列
 的前
的前 项和为
项和为 ,证明:
,证明: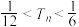 .
.
您最近半年使用:0次
名校
解题方法
2 . 记等差数列 的前n项为
的前n项为 ,
,
 .
.
(1)求 的通项公式;
的通项公式;
(2)若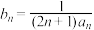 ,求数列
,求数列 的前n项和
的前n项和 .
.
 的前n项为
的前n项为 ,
,
 .
.(1)求
 的通项公式;
的通项公式;(2)若
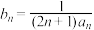 ,求数列
,求数列 的前n项和
的前n项和 .
.
您最近半年使用:0次
名校
解题方法
3 . 已知数列 前
前 项和
项和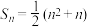 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前
的前 项和
项和 .
.
 前
前 项和
项和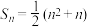 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 的前
的前 项和
项和 .
.
您最近半年使用:0次
4 . 若实数集 对任何
对任何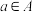 ,
, ,均有
,均有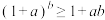 ,则称
,则称 具有伯努利型关系.
具有伯努利型关系.
(1)若集合 ,
, 表示自然数集,判断
表示自然数集,判断 是否具有伯努利型关系;
是否具有伯努利型关系;
(2)设集合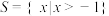 ,
, ,若
,若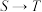 具有伯努利型关系,求非负实数
具有伯努利型关系,求非负实数 的取值范围;
的取值范围;
(3)设 为正整数,利用(2)中结论证明下面不等式:
为正整数,利用(2)中结论证明下面不等式: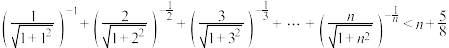 .
.
 对任何
对任何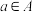 ,
, ,均有
,均有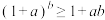 ,则称
,则称 具有伯努利型关系.
具有伯努利型关系.(1)若集合
 ,
, 表示自然数集,判断
表示自然数集,判断 是否具有伯努利型关系;
是否具有伯努利型关系;(2)设集合
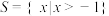 ,
, ,若
,若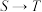 具有伯努利型关系,求非负实数
具有伯努利型关系,求非负实数 的取值范围;
的取值范围;(3)设
 为正整数,利用(2)中结论证明下面不等式:
为正整数,利用(2)中结论证明下面不等式: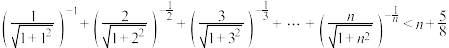 .
.
您最近半年使用:0次
5 . 若数列 满足
满足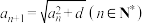 ,其中
,其中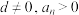 ,则称数列
,则称数列 为
为 数列.已知数列
数列.已知数列 为
为 数列,当
数列,当 时.
时.
(1)求证:数列 是等差数列,并写出数列
是等差数列,并写出数列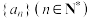 的通项公式;
的通项公式;
(2)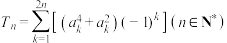 ,求
,求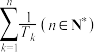 .
.
 满足
满足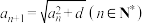 ,其中
,其中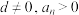 ,则称数列
,则称数列 为
为 数列.已知数列
数列.已知数列 为
为 数列,当
数列,当 时.
时.(1)求证:数列
 是等差数列,并写出数列
是等差数列,并写出数列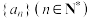 的通项公式;
的通项公式;(2)
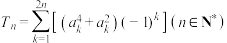 ,求
,求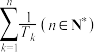 .
.
您最近半年使用:0次
6 . 设 是各项为正的无穷数列,若对于
是各项为正的无穷数列,若对于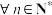 ,
,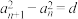 (d:为非零常数),则称数列
(d:为非零常数),则称数列 为等方差数列.那么( )
为等方差数列.那么( )
 是各项为正的无穷数列,若对于
是各项为正的无穷数列,若对于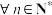 ,
,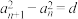 (d:为非零常数),则称数列
(d:为非零常数),则称数列 为等方差数列.那么( )
为等方差数列.那么( )A.若 是等方差数列,则 是等方差数列,则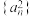 是等差数列 是等差数列 |
B.数列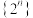 为等方差数列 为等方差数列 |
C.若 是等方差数列,则数列 是等方差数列,则数列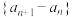 中存在小于1的项 中存在小于1的项 |
D.若 是等方差数列,则存在正整数n,使得 是等方差数列,则存在正整数n,使得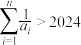 |
您最近半年使用:0次
7 . 已知等差数列 的前
的前 项和为
项和为 ,且
,且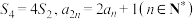 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 满足
满足 ,令
,令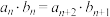 ,求证:
,求证: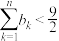 .
.
 的前
的前 项和为
项和为 ,且
,且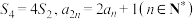 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 满足
满足 ,令
,令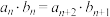 ,求证:
,求证: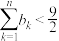 .
.
您最近半年使用:0次
昨日更新
|
1032次组卷
|
2卷引用:浙江省杭州市2024届高三下学期4月教学质量检测数学试题
8 . 已知函数 的定义域为
的定义域为 ,且对任意的
,且对任意的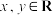 ,都有
,都有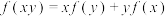 ,若
,若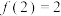 ,则下列说法正确的是( )
,则下列说法正确的是( )
 的定义域为
的定义域为 ,且对任意的
,且对任意的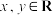 ,都有
,都有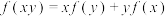 ,若
,若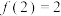 ,则下列说法正确的是( )
,则下列说法正确的是( )A.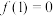 | B. 的图象关于y轴对称 的图象关于y轴对称 |
C.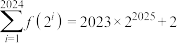 | D. |
您最近半年使用:0次
9 . 已知数列 满足
满足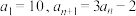 .
.
(1)求 的通项公式;
的通项公式;
(2)若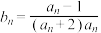 ,记数列
,记数列 的前
的前 项和为
项和为 ,求证:
,求证: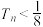 .
.
 满足
满足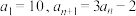 .
.(1)求
 的通项公式;
的通项公式;(2)若
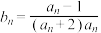 ,记数列
,记数列 的前
的前 项和为
项和为 ,求证:
,求证: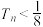 .
.
您最近半年使用:0次
10 . 已知数列 满足
满足 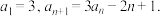
(1)求证: 为等比数列;
为等比数列;
(2)数列 的前n项和为
的前n项和为 ,求数列
,求数列 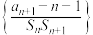 的前n项和
的前n项和 .
.
 满足
满足 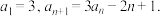
(1)求证:
 为等比数列;
为等比数列;(2)数列
 的前n项和为
的前n项和为 ,求数列
,求数列 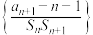 的前n项和
的前n项和 .
.
您最近半年使用:0次



