解题方法
1 . 已知椭圆C: 的右顶点为
的右顶点为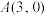 ,离心率为
,离心率为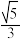 ,过点
,过点 的直线l与C交于M,N两点.
的直线l与C交于M,N两点.
(1)若C的上顶点为B,直线BM,BN的斜率分别为 ,
, ,求
,求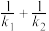 的值;
的值;
(2)过点M且垂直于x轴的直线交直线AN于点Q,证明:线段MQ的中点在定直线上.
 的右顶点为
的右顶点为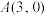 ,离心率为
,离心率为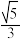 ,过点
,过点 的直线l与C交于M,N两点.
的直线l与C交于M,N两点.(1)若C的上顶点为B,直线BM,BN的斜率分别为
 ,
, ,求
,求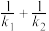 的值;
的值;(2)过点M且垂直于x轴的直线交直线AN于点Q,证明:线段MQ的中点在定直线上.
您最近一年使用:0次
今日更新
|
11次组卷
|
2卷引用:陕西省铜川市王益中学2024届高三下学期高考猜题信息卷(二)文科数学试题
2 . 已知双曲线 的右焦点为
的右焦点为 ,双曲线
,双曲线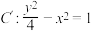 的上焦点为
的上焦点为 ,直线
,直线 ,且
,且 既是
既是 的渐近线也是
的渐近线也是 的渐近线.
的渐近线.
(1)求 的方程;
的方程;
(2)过 作与
作与 轴不垂直的直线与
轴不垂直的直线与 的右支交于点
的右支交于点 ,若点
,若点 在
在 轴上,且
轴上,且 ,求证:
,求证: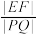 为定值,并求出该定值.
为定值,并求出该定值.
 的右焦点为
的右焦点为 ,双曲线
,双曲线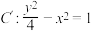 的上焦点为
的上焦点为 ,直线
,直线 ,且
,且 既是
既是 的渐近线也是
的渐近线也是 的渐近线.
的渐近线.(1)求
 的方程;
的方程;(2)过
 作与
作与 轴不垂直的直线与
轴不垂直的直线与 的右支交于点
的右支交于点 ,若点
,若点 在
在 轴上,且
轴上,且 ,求证:
,求证: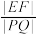 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
解题方法
3 . 已知直线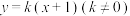 与椭圆
与椭圆 交于两点
交于两点 ,椭圆
,椭圆 的左、右顶点分别为
的左、右顶点分别为 ,直线
,直线 与直线
与直线 ,
, 及
及 轴分别交于点
轴分别交于点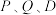 ,则( )
,则( )
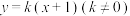 与椭圆
与椭圆 交于两点
交于两点 ,椭圆
,椭圆 的左、右顶点分别为
的左、右顶点分别为 ,直线
,直线 与直线
与直线 ,
, 及
及 轴分别交于点
轴分别交于点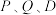 ,则( )
,则( )A.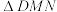 的周长为 的周长为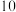 |
B.直线 , , , , , , 的斜率之积为定值 的斜率之积为定值 |
C.当 时,线段 时,线段 的中点到直线 的中点到直线 的距离为 的距离为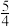 |
D.若 ,则 ,则 的取值范围是 的取值范围是 |
您最近一年使用:0次
解题方法
4 . 已知曲线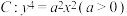 与直线
与直线 有3个公共点,点
有3个公共点,点 是曲线
是曲线 上关于
上关于 轴对称的两动点(点
轴对称的两动点(点 在第一象限),点
在第一象限),点 是
是 轴上关于原点对称的两定点(点
轴上关于原点对称的两定点(点 在
在 轴正半轴上),若
轴正半轴上),若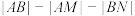 为定值,则该定值为( )
为定值,则该定值为( )
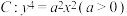 与直线
与直线 有3个公共点,点
有3个公共点,点 是曲线
是曲线 上关于
上关于 轴对称的两动点(点
轴对称的两动点(点 在第一象限),点
在第一象限),点 是
是 轴上关于原点对称的两定点(点
轴上关于原点对称的两定点(点 在
在 轴正半轴上),若
轴正半轴上),若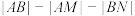 为定值,则该定值为( )
为定值,则该定值为( )| A.8 | B.16 | C. | D.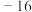 |
您最近一年使用:0次
5 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、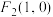 ,
, 在椭圆
在椭圆 上,且
上,且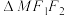 面积的最大值为
面积的最大值为 .
.
(1)求椭圆 的方程;
的方程;
(2)直线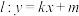 与椭圆
与椭圆 相交于P,Q两点,且
相交于P,Q两点,且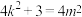 ,求证:
,求证: (
( 为坐标原点)的面积为定值.
为坐标原点)的面积为定值.
 的左、右焦点分别为
的左、右焦点分别为 、
、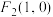 ,
, 在椭圆
在椭圆 上,且
上,且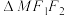 面积的最大值为
面积的最大值为 .
.(1)求椭圆
 的方程;
的方程;(2)直线
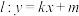 与椭圆
与椭圆 相交于P,Q两点,且
相交于P,Q两点,且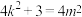 ,求证:
,求证: (
( 为坐标原点)的面积为定值.
为坐标原点)的面积为定值.
您最近一年使用:0次
解题方法
6 . 已知椭圆 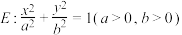 点 P 为E 上落在第一象限的动点,P 关于原点对称的点为 Q,点 A 在E 上满足.
点 P 为E 上落在第一象限的动点,P 关于原点对称的点为 Q,点 A 在E 上满足.  .记直线 PQ,AQ,AP 的斜率分别为
.记直线 PQ,AQ,AP 的斜率分别为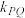 ,
,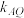 ,
,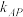 .且满足.
.且满足. 
(1)证明: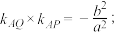
(2)求椭圆E 的离心率;
(3)若 ,求
,求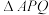 面积的最大值.
面积的最大值.
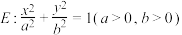 点 P 为E 上落在第一象限的动点,P 关于原点对称的点为 Q,点 A 在E 上满足.
点 P 为E 上落在第一象限的动点,P 关于原点对称的点为 Q,点 A 在E 上满足.  .记直线 PQ,AQ,AP 的斜率分别为
.记直线 PQ,AQ,AP 的斜率分别为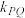 ,
,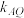 ,
,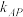 .且满足.
.且满足. 
(1)证明:
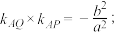
(2)求椭圆E 的离心率;
(3)若
 ,求
,求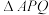 面积的最大值.
面积的最大值.
您最近一年使用:0次
解题方法
7 . 已知曲线 上的点
上的点 满足
满足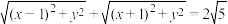 ,曲线
,曲线 过点
过点 的切线与直线
的切线与直线 相交于
相交于 点.
点.
(1)求曲线 的标准方程;
的标准方程;
(2)以 为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
 上的点
上的点 满足
满足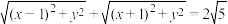 ,曲线
,曲线 过点
过点 的切线与直线
的切线与直线 相交于
相交于 点.
点.(1)求曲线
 的标准方程;
的标准方程;(2)以
 为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
8 . 已知点 ,
, 分别为椭圆
分别为椭圆 :
: 的左顶点和右焦点(椭圆的左顶点
的左顶点和右焦点(椭圆的左顶点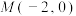 ,右焦点
,右焦点 .),直线
.),直线 过点
过点 且交椭圆
且交椭圆 于P,Q两点,设直线
于P,Q两点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, .
.
(1)求椭圆 的离心率;
的离心率;
(2)是否存在直线 ,使得
,使得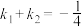 ,若存在,求出直线
,若存在,求出直线 的方程;不存在,说明理由.
的方程;不存在,说明理由.
 ,
, 分别为椭圆
分别为椭圆 :
: 的左顶点和右焦点(椭圆的左顶点
的左顶点和右焦点(椭圆的左顶点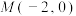 ,右焦点
,右焦点 .),直线
.),直线 过点
过点 且交椭圆
且交椭圆 于P,Q两点,设直线
于P,Q两点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, .
.(1)求椭圆
 的离心率;
的离心率;(2)是否存在直线
 ,使得
,使得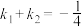 ,若存在,求出直线
,若存在,求出直线 的方程;不存在,说明理由.
的方程;不存在,说明理由.
您最近一年使用:0次
解题方法
9 . 已知椭圆 ,过点
,过点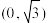 ,
, ,
, 分别是
分别是 的左顶点和下顶点,
的左顶点和下顶点, 是
是 右焦点,
右焦点, .
.
(1)求 的方程;
的方程;
(2)过点 的直线与椭圆
的直线与椭圆 交于点
交于点 ,
, ,直线
,直线 ,
, 分别与直线
分别与直线 交于不同的两点
交于不同的两点 ,
, .设直线
.设直线 ,
,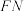 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 ,过点
,过点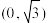 ,
, ,
, 分别是
分别是 的左顶点和下顶点,
的左顶点和下顶点, 是
是 右焦点,
右焦点, .
.(1)求
 的方程;
的方程;(2)过点
 的直线与椭圆
的直线与椭圆 交于点
交于点 ,
, ,直线
,直线 ,
, 分别与直线
分别与直线 交于不同的两点
交于不同的两点 ,
, .设直线
.设直线 ,
,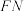 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
10 . 已知动圆M经过定点 ,且与圆
,且与圆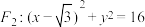 内切.
内切.
(1)求动圆圆心M的轨迹C的方程;
(2)设轨迹C与x轴从左到右的交点为点A,B,点P为轨迹C上异于A,B的动点,设直线PB交直线 于点T,连接AT交轨迹C于点Q;直线AP,AQ的斜率分别为
于点T,连接AT交轨迹C于点Q;直线AP,AQ的斜率分别为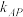 ,
,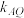 .
.
(i)求证: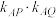 为定值;
为定值;
(ii)设直线 ,证明:直线PQ过定点.
,证明:直线PQ过定点.
 ,且与圆
,且与圆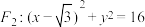 内切.
内切.(1)求动圆圆心M的轨迹C的方程;
(2)设轨迹C与x轴从左到右的交点为点A,B,点P为轨迹C上异于A,B的动点,设直线PB交直线
 于点T,连接AT交轨迹C于点Q;直线AP,AQ的斜率分别为
于点T,连接AT交轨迹C于点Q;直线AP,AQ的斜率分别为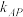 ,
,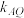 .
.(i)求证:
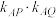 为定值;
为定值;(ii)设直线
 ,证明:直线PQ过定点.
,证明:直线PQ过定点.
您最近一年使用:0次



