1 . 已知函数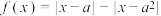 .
.
(1)当 时,求不等式
时,求不等式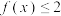 的解集;
的解集;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
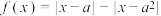 .
.(1)当
 时,求不等式
时,求不等式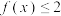 的解集;
的解集;(2)若
 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-06更新
|
85次组卷
|
2卷引用:陕西省铜川市王益中学2024届高三下学期模拟预测文科数学试题
名校
2 . 设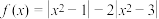 ,
,
(1)解不等式:
(2)设 的最大值为
的最大值为 ,已知正数
,已知正数 和
和 满足
满足 ,令
,令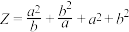 ,求
,求 的最小值.
的最小值.
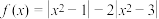 ,
,(1)解不等式:

(2)设
 的最大值为
的最大值为 ,已知正数
,已知正数 和
和 满足
满足 ,令
,令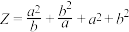 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-06-06更新
|
174次组卷
|
3卷引用:四川省成都石室中学2024届高三下学期高考适应性考试(一)理科数学试题
3 . 已知函数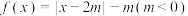 .
.
(1)求不等式 的解集;
的解集;
(2)当 时,函数
时,函数 的最小值为
的最小值为 ,若非零实数
,若非零实数 满足
满足 ,证明:
,证明: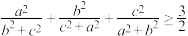 .
.
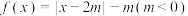 .
.(1)求不等式
 的解集;
的解集;(2)当
 时,函数
时,函数 的最小值为
的最小值为 ,若非零实数
,若非零实数 满足
满足 ,证明:
,证明: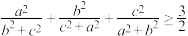 .
.
您最近一年使用:0次
名校
解题方法
4 . 已知函数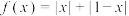 的最小值是
的最小值是 .
.
(1)求 的值;
的值;
(2)若 ,证明:
,证明: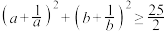 .
.
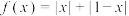 的最小值是
的最小值是 .
.(1)求
 的值;
的值;(2)若
 ,证明:
,证明: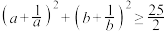 .
.
您最近一年使用:0次
2024-05-27更新
|
114次组卷
|
2卷引用:四川省绵阳南山中学2024届高三下学期高考仿真演练1理科数学试题
名校
解题方法
5 . 已知函数 .
.
(1)若 ,求不等式
,求不等式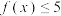 的解集;
的解集;
(2)若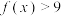 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(1)若
 ,求不等式
,求不等式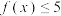 的解集;
的解集;(2)若
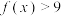 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024·全国·模拟预测
名校
解题方法
6 . 在平面直角坐标系中,两点 的“曼哈顿距离”定义为
的“曼哈顿距离”定义为 ,记为
,记为 ,如点
,如点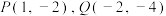 的“曼哈顿距离”为5,记为
的“曼哈顿距离”为5,记为
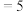 .
.
(1)若点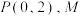 是满足
是满足
 的动点
的动点 的集合,求点集
的集合,求点集 所占区域的面积;
所占区域的面积;
(2)若动点 在直线
在直线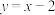 上,动点
上,动点 在函数
在函数 的图象上,求
的图象上,求 的最小值;
的最小值;
(3)设点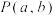 ,动点
,动点 在函数
在函数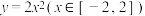 的图象上,
的图象上, 的最大值记为
的最大值记为 ,求
,求 的最小值.
的最小值.
 的“曼哈顿距离”定义为
的“曼哈顿距离”定义为 ,记为
,记为 ,如点
,如点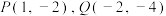 的“曼哈顿距离”为5,记为
的“曼哈顿距离”为5,记为
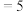 .
.(1)若点
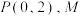 是满足
是满足
 的动点
的动点 的集合,求点集
的集合,求点集 所占区域的面积;
所占区域的面积;(2)若动点
 在直线
在直线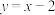 上,动点
上,动点 在函数
在函数 的图象上,求
的图象上,求 的最小值;
的最小值;(3)设点
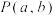 ,动点
,动点 在函数
在函数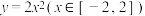 的图象上,
的图象上, 的最大值记为
的最大值记为 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-04-23更新
|
229次组卷
|
3卷引用:2024年普通高等学校招生全国统一考试·押题卷数学(二)
名校
7 . 已知函数 .
.
(1)求 的最小值;
的最小值;
(2)若 的最小值为
的最小值为 ,正实数a,b,c满足
,正实数a,b,c满足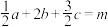 ,求证:
,求证: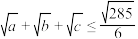
 .
.(1)求
 的最小值;
的最小值;(2)若
 的最小值为
的最小值为 ,正实数a,b,c满足
,正实数a,b,c满足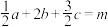 ,求证:
,求证: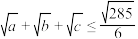
您最近一年使用:0次
2024-04-12更新
|
188次组卷
|
4卷引用:陕西省安康市汉滨区2024届高三下学期高考模拟(五)文科数学试题
2024·全国·模拟预测
解题方法
8 . 已知函数 .
.
(1)若不等式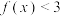 的解集包含
的解集包含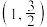 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若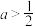 ,且
,且 的最小值为
的最小值为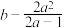 ,求实数
,求实数 的最小值.
的最小值.
 .
.(1)若不等式
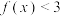 的解集包含
的解集包含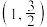 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
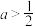 ,且
,且 的最小值为
的最小值为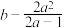 ,求实数
,求实数 的最小值.
的最小值.
您最近一年使用:0次
2024·全国·模拟预测
9 . 已知函数 .
.
(1)求不等式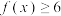 的解集;
的解集;
(2)若不等式 的解集为
的解集为 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)求不等式
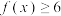 的解集;
的解集;(2)若不等式
 的解集为
的解集为 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
10 . 已知函数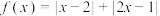 .
.
(1)求 的最小值;
的最小值;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
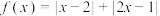 .
.(1)求
 的最小值;
的最小值;(2)若
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-07更新
|
247次组卷
|
3卷引用:陕西省2024届高三下学期2月大联考数学试题(全国乙卷)



