解题方法
1 . 已知函数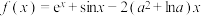 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是
的取值范围是_____________ .
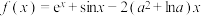 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
解题方法
2 . 已知函数 ,则“
,则“ ”是“
”是“ 在
在 上单调递增”的( )
上单调递增”的( )
 ,则“
,则“ ”是“
”是“ 在
在 上单调递增”的( )
上单调递增”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
3 . 已知函数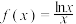 .
.
(1)若方程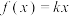 有两解,求实数
有两解,求实数 的取值范围;
的取值范围;
(2)若对任意的 ,不等式
,不等式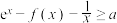 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
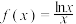 .
.(1)若方程
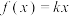 有两解,求实数
有两解,求实数 的取值范围;
的取值范围;(2)若对任意的
 ,不等式
,不等式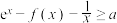 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
76次组卷
|
2卷引用:河北省唐山市百师联盟2023-2024学年高二下学期期末联考数学试卷
名校
解题方法
4 . 已知函数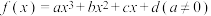 在
在 处取到极大值1,则以下结论正确的是( )
处取到极大值1,则以下结论正确的是( )
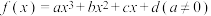 在
在 处取到极大值1,则以下结论正确的是( )
处取到极大值1,则以下结论正确的是( )A.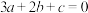 | B.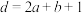 |
C.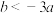 | D.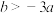 |
您最近一年使用:0次
7日内更新
|
175次组卷
|
3卷引用:广东省东莞市2023-2024学年高二下学期7月期末教学质量检查数学试题
解题方法
5 . 已知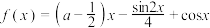 是
是 上的增函数,则实数
上的增函数,则实数 的取值范围是( )
的取值范围是( )
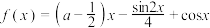 是
是 上的增函数,则实数
上的增函数,则实数 的取值范围是( )
的取值范围是( )A.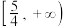 | B.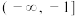 | C.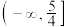 | D. |
您最近一年使用:0次
名校
6 . 若函数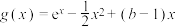 存在单调递减区间,则实数
存在单调递减区间,则实数 的取值范围是( )
的取值范围是( )
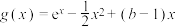 存在单调递减区间,则实数
存在单调递减区间,则实数 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
您最近一年使用:0次
7日内更新
|
295次组卷
|
2卷引用:广东省四校(华附、省实、广雅、深中)2023-2024学年高二下学期期末联考数学试题
解题方法
7 . 若函数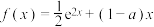 在区间
在区间 上单调递增,则实数a的取值范围为
上单调递增,则实数a的取值范围为_________
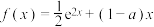 在区间
在区间 上单调递增,则实数a的取值范围为
上单调递增,则实数a的取值范围为
您最近一年使用:0次
名校
解题方法
8 . 已知函数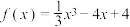 在
在 上的最大值为4,则实数a的取值范围为( )
上的最大值为4,则实数a的取值范围为( )
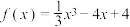 在
在 上的最大值为4,则实数a的取值范围为( )
上的最大值为4,则实数a的取值范围为( )A.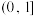 | B.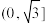 | C. | D.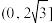 |
您最近一年使用:0次
名校
解题方法
9 . 已知函数 .
.
(1)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)若函数 有两个不同的极值点
有两个不同的极值点 ,求证:
,求证: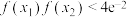 .
.
 .
.(1)若函数
 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;(2)若函数
 有两个不同的极值点
有两个不同的极值点 ,求证:
,求证: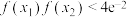 .
.
您最近一年使用:0次
解题方法
10 . 若函数 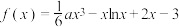 为定义域内的单调递增函数,则实数a的取值范围是( )
为定义域内的单调递增函数,则实数a的取值范围是( )
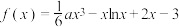 为定义域内的单调递增函数,则实数a的取值范围是( )
为定义域内的单调递增函数,则实数a的取值范围是( )A. | B.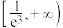 | C.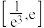 | D. |
您最近一年使用:0次



