23-24高二下·上海·期末
解题方法
1 . 如图所示,在三棱柱 中,
中,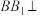 平面
平面 ,
,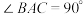 ,
,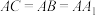 ,
, 是
是 的中点.
的中点. 与
与 所成的角的大小;
所成的角的大小;
(2)若 为
为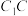 中点,求二面角
中点,求二面角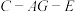 的正切值.
的正切值.
 中,
中,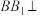 平面
平面 ,
,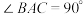 ,
,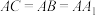 ,
, 是
是 的中点.
的中点.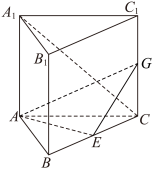
 与
与 所成的角的大小;
所成的角的大小;(2)若
 为
为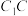 中点,求二面角
中点,求二面角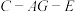 的正切值.
的正切值.
您最近一年使用:0次
23-24高二下·上海·期末
2 . 如图,在三棱柱 中,
中, 底面
底面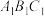 ,
, ,
,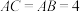 ,
,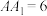 ,点
,点 ,
, 分别为
分别为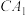 与
与 的中点.
的中点. 平面
平面 .
.
(2)求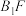 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 底面
底面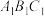 ,
, ,
,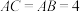 ,
,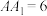 ,点
,点 ,
, 分别为
分别为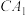 与
与 的中点.
的中点.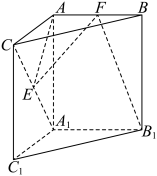
 平面
平面 .
.(2)求
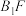 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
3 . 已知 、
、 是双曲线
是双曲线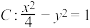 的两点,
的两点, 的中点
的中点 的坐标为
的坐标为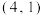 .
.
(1)求直线 的方程;
的方程;
(2)求 两点间距离.
两点间距离.
 、
、 是双曲线
是双曲线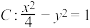 的两点,
的两点, 的中点
的中点 的坐标为
的坐标为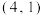 .
.(1)求直线
 的方程;
的方程;(2)求
 两点间距离.
两点间距离.
您最近一年使用:0次
名校
4 . 如图,在直三棱柱 中,
中, ,
,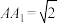 ,
, ,
, 为
为 的中点.
的中点.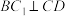 ;
;
(2)设 为
为 的中点,
的中点, 在棱
在棱 上,满足
上,满足 平面
平面 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.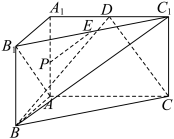
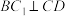 ;
;(2)设
 为
为 的中点,
的中点, 在棱
在棱 上,满足
上,满足 平面
平面 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
7日内更新
|
279次组卷
|
4卷引用:【北京专用】高二下学期期末模拟测试B卷
解题方法
5 . 如图,正方体 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且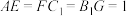 ,
, 是棱
是棱 上一点.
上一点. ,
, ,
, ,
, 四点共面;
四点共面;
(2)若平面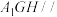 平面
平面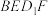 ,求证:
,求证: 为
为 的中点.
的中点.
(3)求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且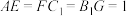 ,
, 是棱
是棱 上一点.
上一点.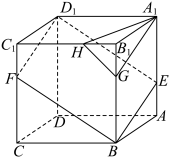
 ,
, ,
, ,
, 四点共面;
四点共面;(2)若平面
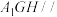 平面
平面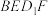 ,求证:
,求证: 为
为 的中点.
的中点.(3)求平面
 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
您最近一年使用:0次
7日内更新
|
121次组卷
|
2卷引用:海南省2020-2021学年高二下学期期末考试数学试题
解题方法
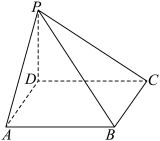
6 . 如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
,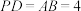 ,且
,且 .
. ;
;
(2)当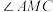 为钝角时,求实数
为钝角时,求实数 的取值范围;
的取值范围;
(3)若二面角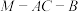 的大小为
的大小为 ,求点
,求点 到平面
到平面 的距离.
的距离.
 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
,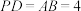 ,且
,且 .
.
 ;
;(2)当
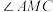 为钝角时,求实数
为钝角时,求实数 的取值范围;
的取值范围;(3)若二面角
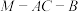 的大小为
的大小为 ,求点
,求点 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
7 . 已知椭圆 的离心率为
的离心率为 ,左、右顶点分别为
,左、右顶点分别为 ,左、右焦点分别为
,左、右焦点分别为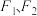 ,过右焦点
,过右焦点 的直线
的直线 交椭圆于点
交椭圆于点 ,且
,且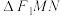 的周长为16.
的周长为16. 的标准方程;
的标准方程;
(2)记直线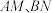 的斜率分别为
的斜率分别为 ,证明:
,证明: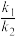 为定值:
为定值:
(3)记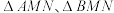 的面积分别为
的面积分别为 ,求
,求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,左、右顶点分别为
,左、右顶点分别为 ,左、右焦点分别为
,左、右焦点分别为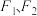 ,过右焦点
,过右焦点 的直线
的直线 交椭圆于点
交椭圆于点 ,且
,且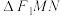 的周长为16.
的周长为16.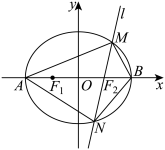
 的标准方程;
的标准方程;(2)记直线
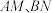 的斜率分别为
的斜率分别为 ,证明:
,证明: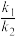 为定值:
为定值:(3)记
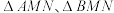 的面积分别为
的面积分别为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 设点 为抛物线
为抛物线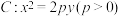 的焦点,过点
的焦点,过点 且斜率为
且斜率为 的直线与
的直线与 交于
交于 两点(
两点( 为坐标原点).
为坐标原点).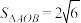
(1)求抛物线 的方程;
的方程;
(2)过点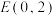 作两条斜率分别为
作两条斜率分别为 的直线
的直线 ,它们分别与抛物线
,它们分别与抛物线 交于点
交于点 和
和 .已知
.已知 ,问:是否存在实数
,问:是否存在实数 ,使得
,使得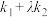 为定值?若存在,求
为定值?若存在,求 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 为抛物线
为抛物线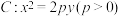 的焦点,过点
的焦点,过点 且斜率为
且斜率为 的直线与
的直线与 交于
交于 两点(
两点( 为坐标原点).
为坐标原点).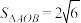
(1)求抛物线
 的方程;
的方程;(2)过点
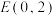 作两条斜率分别为
作两条斜率分别为 的直线
的直线 ,它们分别与抛物线
,它们分别与抛物线 交于点
交于点 和
和 .已知
.已知 ,问:是否存在实数
,问:是否存在实数 ,使得
,使得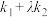 为定值?若存在,求
为定值?若存在,求 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次
名校
9 . 已知椭圆 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,离心率
,离心率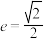 ,直线FB过点
,直线FB过点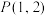 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过点 的直线
的直线 与椭圆
与椭圆 相交于M,N两点(M、N都不在坐标轴上),若
相交于M,N两点(M、N都不在坐标轴上),若 ,求直线
,求直线 的方程.
的方程.
 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,离心率
,离心率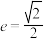 ,直线FB过点
,直线FB过点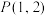 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 的直线
的直线 与椭圆
与椭圆 相交于M,N两点(M、N都不在坐标轴上),若
相交于M,N两点(M、N都不在坐标轴上),若 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024-06-13更新
|
809次组卷
|
2卷引用:四川省成都市树德中学2023-2024学年高二下学期期末数学试题
名校
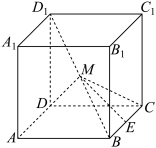
10 . 如图,正方体 的棱长为2,
的棱长为2, 为
为 的中点,点
的中点,点 在
在 上,
上, .
. 为
为 的中点;
的中点;
(2)求直线 与平面
与平面 所成角的大小.
所成角的大小.
 的棱长为2,
的棱长为2, 为
为 的中点,点
的中点,点 在
在 上,
上, .
.
 为
为 的中点;
的中点;(2)求直线
 与平面
与平面 所成角的大小.
所成角的大小.
您最近一年使用:0次



